조합회로에는 여러가지 기본 회로들이 존재한다. 회로들을 살펴보며 그것들이 가지는 특징과 결과값에 대하여 알아보자. 먼저 AND 회로를 살펴보자.
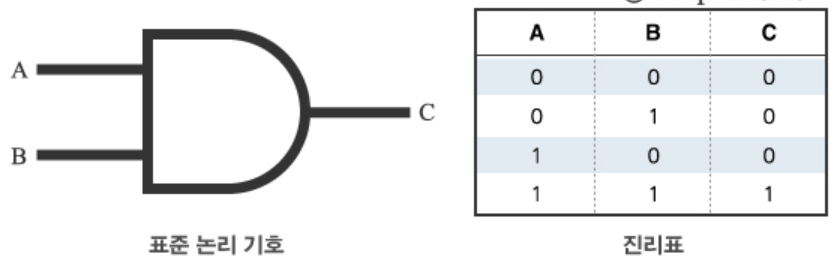
and연산의 경우, 여러 input의 값 중 하나의 값이 0이면, 그 결과는 0이다. 따라서, 어떤 input이 들어오던지, 모든 input이 1일때만 1의 값을 가지게 된다.
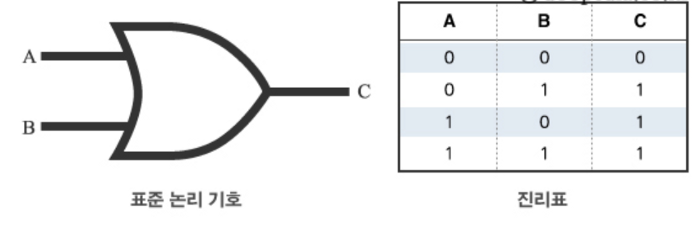
이와는 반대로, or연산의 경우는, 어느 값중에 하나만 1이어도 결과 값이 1이 된다.
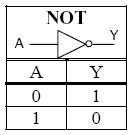
마지막으로 not 연산의 경우에는, 경우의 수가 2가지 밖에 없고, x를 넣었을 때 그와 반대되는 값이 나오게 된다.
이러하게, 회로에서 input의 모든 가능한 경우에 대한 결과값을 나타내는 표를 진리표라 한다.
즉, 회로(logic)의 동작을 표로(input-output관계를 표로) 보이는 것 : 진리표(truth table) 이다.
여기서 만약, A회로와 B회로가 있다고 가정하자. A회로와 B회로의 모든 입력이 같고, 또 두 회로의 결과값이 같다면, 이 두 회로를 같은 동작을 하는 등가회로(equivalent logic) 라고 한다.
또한, A회로가 input의 값을 4개 가지고 있다고 생각해보자. 이때에, input의 모든 조합의 가짓수가 4개이므로 전체 가능한 인풋의 조합은 2의 4승이 된다. 따라서, 전체 조합의 갯수는 16개가 된다. 따라서, B의 전체 16개 조합이 A와 같고, 그 결과또한 같으면, 이 두 회로는 같은 동작을 한다고 말할 수 있다.
부울 대수의 공준과 정리

부울 대수에는 크게는 다음과 같은 공준과 정리가 존재한다.
(항등법칙 1번의 경우 1 + A = 1이다.)
예시로 아래의 문제를 살펴보자.
x + xy =
이 때에, x 와 x * 1은 동일한 값을 지니므로 다음과 같이 치환한다.
x 1 + x y =
x의 곱이 두수의 곱에 공존하므로, 밖으로 빼준다.
x * (1 + y) =
이것을, 항등법칙 1번으로 보자면
x * (1) =
이며, 따라서 값은 1이 된다.
이와 같이, 공준과 정리를 이용하여 식을 짧게 만들 수 있다.
다른 예시로는 다음과 같은 것이 있다.
x (x + y) = x x + x y = x + x y = x
다음은 드모르간의 법칙에 대해 살펴보자. 드모르간 법칙을 부울함수로 나타내자면 이렇게된다.
(x+y)' = F == x'y' = G
드모르간 법칙에 따르면, 이 둘의 값은 같다. 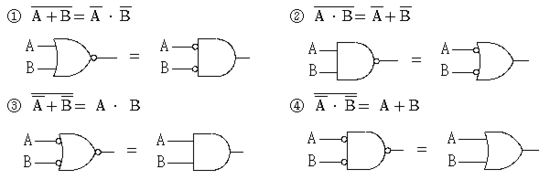
위의 이미지 중에서, 1번에 집중해보자. 이 논리회로를 진리표로 나타내보면 다음과같다.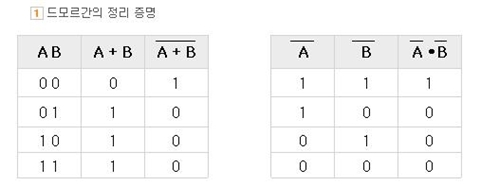
따라서, 모든 input에 대하여 (all possible input combination) output이 동일하므로 이 두 회로는 같은 기능을 의미한다. 즉, (x + y)' = x'y' 이다.
다른 예제로는, 아래의 공식을 간단하게 줄여보자.
F = x'y'z + xyz + x'yz + xy'z
이 값중에서, y'z를 가지고 있는 부분과, yz를 가지고 있는 부분으로 따로 모아보자.
= x'y'z + xy'z + xyz + x'yz
= (x'+x)y'z + (x+x')yz
여기에서, x'과 x를 or하면 1이 되므로
y'z + yz
가 된다. 이걸 다시 묶으면
(y'+y)z
이고, y'+y가 1이므로, F는 z와 같은 진리표를 가지게 된다.
하지만, 왜 간단하게 만들려고 하는가?
위에 식을 그대로 사용한다면, gate로는 AND가 4개, or가 1개 필요하다. 하지만 z를 그대로 가져다 쓰면 gate가 필요하지 않다. 즉, 원래 그대로의 회로를 사용한다면 크기가 커지고, 이것은 전력소모와 발열이 증가함을 의미한다. 이와 같은 것들을 줄일 수 있다는 의미는 즉, 소형화를 할 수 있다는 의미이며, 또 gate의 갯수가 줄어들면 속도 역시 빨라진다. 공식이 간단해지면, 회로가 간단해지고, 회로가 간단해지면 소형화와 최적화가 가능해진다.
부울 함수란 무엇인가
예제 중 F2를 살펴보자.
F2 = x'y'z + x'yz + xy' 이다.
이 공식을 먼저 간단하게 해보자.
F2 = x'y'z + x'yz + xy' = x'z(y'+y) + xy' = x'z + xy'
즉, 이 두 부울함수와 회로는(간단하게 만든 것과 원상태의 것) 같은 기능을 한다고 할 수 있다.
gate의 size와 delay
게이트의 경우, and와 or등이 가장 기본이라 생각할 수 있지만, 회로에서 가장 기본이 되는 회로는 NAND와 NOR, NOT이다. 이들은 다음과 같은 size와 delay를 가진다.
NAND : size : 1AT
delay : 1△t
NOT : size : 1AT
delay : 1△t
NOR : size : 1AT
delay : 1△t
이것들이 기본 size와 기본 delay를 나타낸다고 할 수 있다. 여기서 다시, AND와 OR gate의 size와 delay를 살펴보자.
사실 AND gate는 원래 AND로 되어있는 것이 아니라, NAND에 NOT을 붙여 만든다. 따라서
AND : size : 2AT
delay : 2△t
가 된다. OR도 마찬가지로 NOR에 NOT을 붙여 만든다.
OR : size : 2AT
delay : 2△t
이와같이 AND와 OR의 크기와 딜레이가 크므로 회로를 설계할때는 주로 NAND와 NOR로 많이 설계를 하게된다.
딜레이와 사이즈를 계산하는 법을 알아냈으니, 다시 위의 예제를 살펴보자.
F2 = x'y'z + x'yz + xy'
는, AND3개, OR1개, NOT 2개로 이루어져 있으므로 size는 (3 and) + (1 or) + (2 not) 이 된다. 따라서 (3 2) + (1 2) + (2 1) 이므로, 전체 사이즈는 10AT가 된다.
delay는 기본적으로 worst cast path(가장 긴 path)로 계산하게 된다.
위 식의 worst path는
1NOT + 1AND + 1 OR
이다. 따라서 값은 5△t가 나오게 된다.
다음으로는, 최적화한 식의 size와 delay를 살펴보자.
F2 = xy' + x'z
여기서 크기는 AND 2개 + OR 1 개 + NOT 1개이다.
따라서 size는
size = (22) + (21) + (1*1) = 7이 되므로, 7AT가 된다. 위의 size엿던 10보다 3 작은 크기를 가지게 되었다.
delay로는 1NT + 1AND 1 OR = 5△t이므로, 위 식과 딜레이는 같다는것을 알 수 있다.
변형된 식은 size는 더 작고 delay는 같다. 즉, 이와같이 최적화로 더 작은 size를 가지게 되었다.
