논리 회로에는 두가지 종류가 있는데, 순차회로와 조합회로가 있다. 여기서는, 조합회로에 대하여 집중적으로 알아보자.

인풋과 아웃풋이 있는 어떤 상자를 상상해보자. 인풋은 외부로부터 입력을 받고, 상자 내부에서는 어떠한 처리가 일어난다. 예를 들어, 1 -> A , 2 - > B. 이와 같이, 상자(조합 논리회로) 내부의 어떠한 algorithm 을 통하여 일정한 다른 값을 값을 output으로 가지게 되는데, 이중에서도 특히 상자 내부를 우리는 조합회로라 한다.
또 이러한 조합회로의 예시로, 우리는 인풋과 아웃풋의 관계를 만들 수 있으며 이를 진리표라 한다.
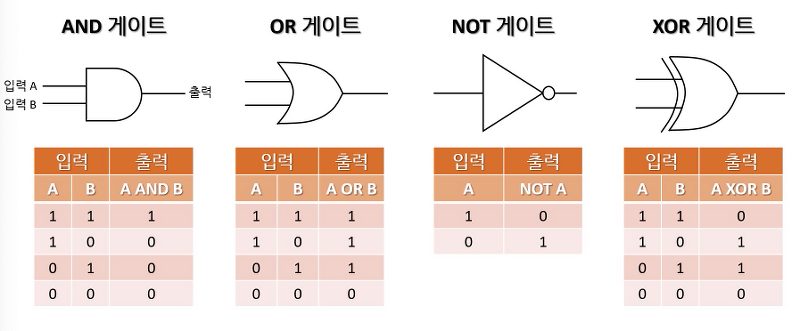
기본적인 게이트로는 AND, OR, NOT 게이트가 있으며 심화적인 게이트로는 XOR 게이트가 있다. 이는 새로운 게이트가 아니라 기존의 게이트를 재조합하여 만들 수 있다.

(위사진은 기본 게이트 (not, and, or)를 가지고 xor을 만드는 것을 보여준다.)
칩 설계는 크게 디지털 회로, 또는 아날로그 회로 설계 둘로 나누어진다. 디지털 회로는 1,0만을 다루는 회로를 디지털 회로라 한다. 아날로그 회로는 연속된 값을 다룬다. 하지만 아날로그 회로는 대중적이지 않기도 하다. 그리고, 이러한 차이는 Digital과 Analog의 차이로도 볼 수 있다.
Digital Analog
구분된 (Discrete) 연속된 값 (continuous)
자연수 : 1, 2, 3, 4 ... 유리수 : 0.001, 0.0002, ...
정수 :-2, -1, 0, 1, 2 ... 무리수 : π=3.141592⋯⋯ , e = 2.71828...
아날로그 값은 연산하는 기계를 Analog computer라고 한다. 또, 구분된 값을 연산하는 것을 Digital computer라고도 하는데, 대부분의 기계가 디지털 컴퓨터이기 때문에, 보통 computer 이라고 표현한다.
인간은 주로 수를 표현할 때 10진수를 사용한다.
10진수 : {0,1,2 ... 9}
하지만, 컴퓨터는 이진수를 사용한다.
2진수 : {0,1}, {off, on}, {hi,lo}
컴퓨터는 전압이 흐르느냐, 높으냐, 전압이 높은가, 낮은가로 밖에 신호를 이해하지 못하기 때문에, 2진수를 쓴다. 이러한 컴퓨터는, 복잡한 연산을 해결하기 위해 필요하다.

이 항목에서, 복잡할 산술을 진행할 값을 입력이라 하고, 논리 회로를 컴퓨터라 하고, 출력을 결과라고 해보자. 논리회로에는 식 (equation)이 있을 것이고, 그것은 algorithm과 같다. 우리는 흔히, 연산을 할때 10진수로 계산하고, 컴퓨터는 2진수 밖에 이해하지 못한다. 따라서, 이진수를 변화(conversion)시킬 방법이 필요하다.
첫번째 예로는, 10진수를 2진수로 변환시키는 방법을 보자.
10진수 <- -> 2진수
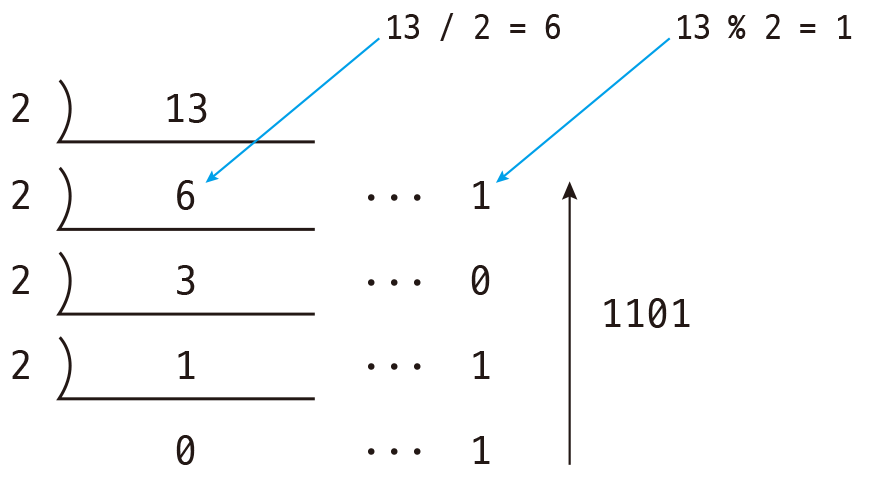
위에 이미지를 보면, 맨처음 13을 2로 나누고, 몫을 아래에 적고 나머지를 오른쪽 하단에 적는다. 아마 이미 2진법을 계산하는 방법을 배운적이 있겠지만, 이렇게 식을 몫이 0이 될때까지 계속해서 진행해준다음에, 아래에서 부터 위로 읽어주면 그 식에 해당하는 2진수로 변환된다.
또한, 사람은 10진법을 사용하며, 컴퓨터는 2진법을 사용한다. 따라서, 10진수에서 2진수로 변환하고 결과를 얻어낸 후, 그 결과값을 다시 10진수로 변환해야 한다. 여기서, 10진수를 10의 지수의 10진수의 곱으로 나타내는 것을 살펴보자.
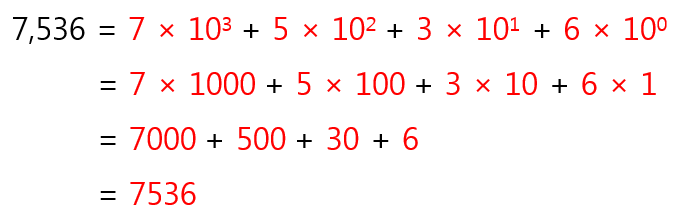
이와같이, 10진수 체계에서 7,536을 나타낼 때에, 이는 각 10의 3제곱, 2제곱, 1제곱, 0제곱의 자릿수로 각각 나타낼 수 있다.
마찬가지로, 2진수 또한 2의 지수의 2진수의 곱 형으로 나타낼 수 있다.
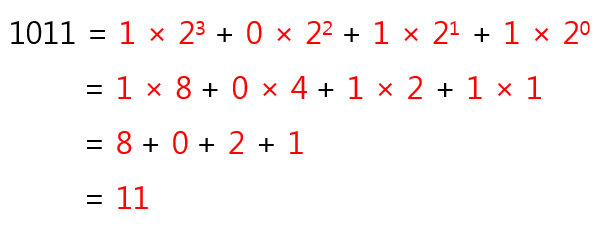
다음과 같이, 1011을 2의 3제곱, 2제곱, 1제곱, 0의 제곱의 자릿수로 나타낼 수 있다.
이때에, 2진수는 컴퓨터가 사용하는 진법이며, 10진법은 사람이 사용하는 진법이다.
이때에, 97(10진법) + 3(10진법) = 100(10진법)
을 컴퓨터로 계산한다고 생각해보자. 먼저 97과 3은 각각 1100001, 그리고 3은 11로 변환될 것이고, 두 수는
1100001
11
; +
ㅡㅡㅡㅡㅡㅡ
1100100
으로 계산될 것이다. 그리고, 1100100은 각각 2의 6제곱, 5제곱, 4제곱, 3제곱, 2제곱, 1제곱, 0제곱 의 자릿수로 계산되고, 이는 각각 64 + 32 + 0 + 0 + 4 + 0 + 0 를 모두 더한 값인 100이 된다.
따라서, 이것이 바로 일종의 조합회로로 얻어낼 수 있는 결과라고 볼 수 있다. 우리는 97과 3을 10진수로 컴퓨터에 넘겨주었고, 컴퓨터는 그것을 연산 후 다시 10진수로 변환하여 출력하였다. 이같은 덧셈을 수행하는 것은 쉬워보이지만 사실 굉장히 복잡한 조합회로로 되어있다.
양수는 이와같이 처리할 수 있다. 하지만, 음수의 경우는 어떨까?
보토으이 경우, 10진수는 이렇게 처리할 수 있다. 밑은 기호로 음수와 양수를 구분한 것이다.
(기호)+ 97 (양수)
(기호)- 97 (음수)
여기에, 이것을 숫자로 이용하여 구분해 보자.
(기호)0 97 (양수)
(기호)9 97 (음수)
0 = positive
9 = negative
이처럼, 기호대신 숫자로도 음수, 양수를 나타낼 수 있다.
여기서, 2진수를 기호로 음수와 양수를 구분한것을 살펴보자.
+ 101
- 101
여기에서, 컴퓨터는 0과 1만을 사용하기 때문에, 기호를 사용할 수 없다. 따라서, 오직 숫자로만 표시해야 한다. 따라서, 맨 윗자리 수가 0이면 양수로, 1이면 음수로 처리한다.
+ 0 101 (양수)
- 1 101 (음수)
여기서, 맨 윗자리는 부호이며, msb라고도 한다. 이것은 most significant bit의 약자이다.
하지만 여기서, 0101과 1101을 더해보자. 값은 10010이 나오고, 예상했던 값인 0을 찾을 수 없다. +5와 -5를 더했더니 -2가 나와 결과값이 틀리게 출력되었다.

모든 숫자들은, 모두 부호와 크기 둘 다를 가지고 있어야 한다. 위의 이미지는 모든 숫자가 가지고 있어야 하는 Sign bit과 Maginitude를 표시한 것이다.
위에서 우리가 계산했듯이 이렇게 sign만을 표시하는 것을 Signed magnitude라 하며 sm이라 한다. 하지만, 위와 같이 Signed magnitude로 계산하게 되면 틀린 값이 나오게 된다. 그래서 나온 것이 1's complement (1의 보수) 라는 개념이다.
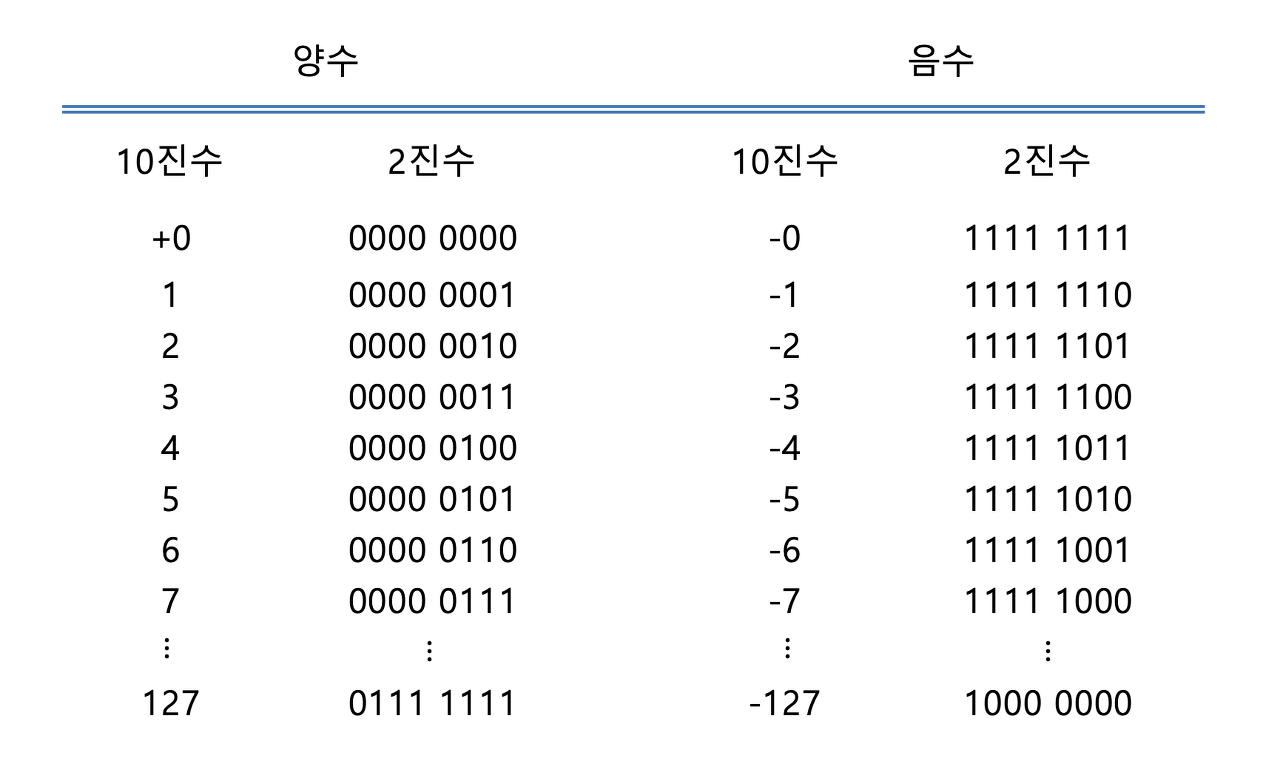
여기서, 1's complement의 특징을 한가지 알아보면, 양수의 경우에는 그대로 이진수대로 읽으면 되지만, 음수의 경우에는 양수로 변환시켜 보아야지만 결과값을 알 수 있다.
여기서, 1의 보수의 문제점은, 0이 양수 0과 음수 0으로 나누어지는 것이 첫번째 문제이다. 개념적으로 양수 0과 음수 0은 존재하지 않는다. 또한, 만약 결과값에 캐리 (자리올림) 이 발생한다면 마지막 결과값에 +1을 해주어야 제대로 된 결과가 나오는 것 또한 문제이다.
[장점]
-
비트만 반전시키면 음수값을 얻을 수 있다.
-
MSB의 성질이 유지가 된다.
-
덧셈만으로 뺄셈을 구현할 수 있어 비교적 회로가 단순해진다.
[단점]
-
캐리가 발생하는 경우를 처리해주어야 한다.
-
-0과 +0을 모두 인지할 수 있도록 처리해주어야 한다.
이와 같은 문제때문에, 2의 보수라는 음수 처리법이 나왔다.
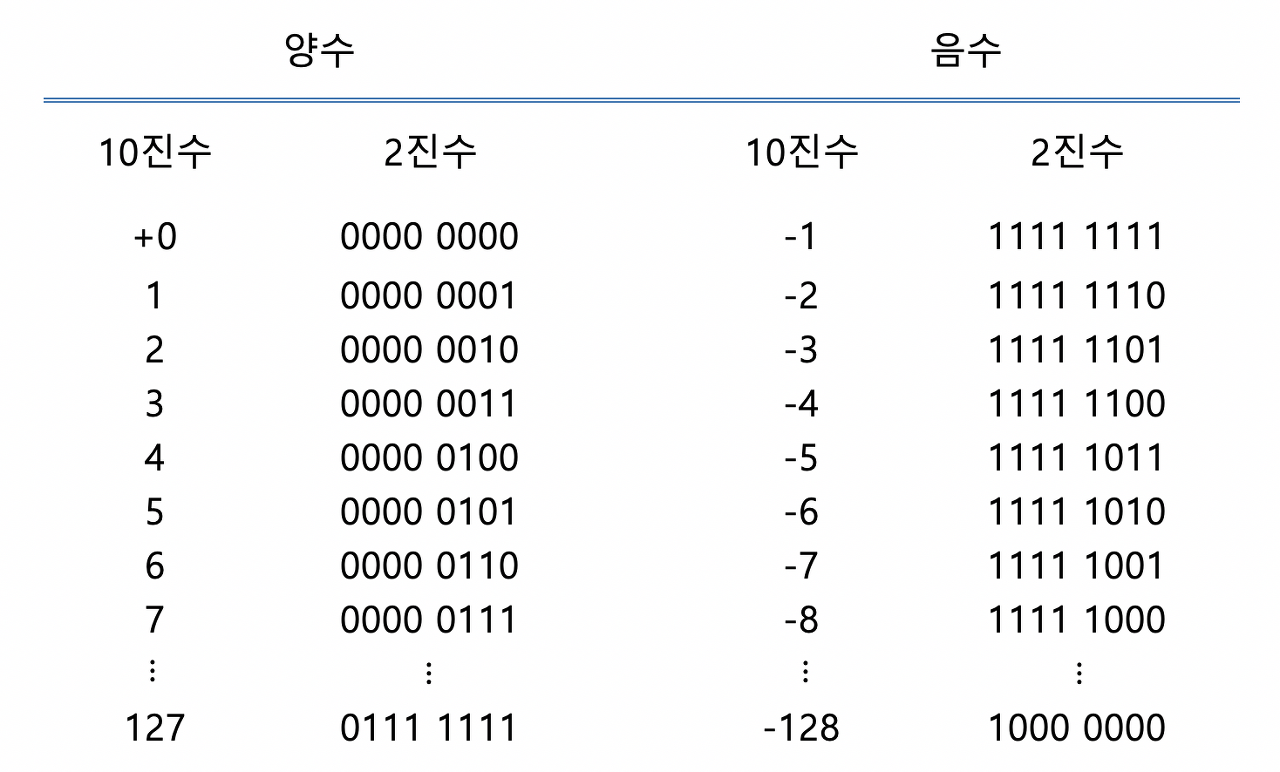
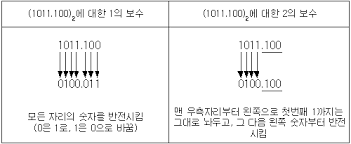
2의 보수를 구하는 방법은, 각 수를 반전시킨 다음, 1을 더해주는 것과 같다.
여기서, +5와 -5를 계산해보자.
0101
1011
ㅡㅡㅡ
0000
옳은 결과값이 나온다. 또한, 2의 보수에서는 0만 존재하고 -0은 없다.
끝내면서, 또한가지 집중해서 생각해볼 점은, Number은 '반드시' Sign(부호) 와 magnitude(크기)가 '둘다' 있어야 한다.
