Sorting algorithm

A sorting algorithm is one of the most important problems in computer science, and it is a problem of rearranging a given dataset by arranging it in a predetermined order.
In actual development, there are quite a few cases where you need to sort and search for irregular data.
For example, suppose that you take balls one by one from a bag containing irregularly numbered balls 1 to 10 and arrange the balls in order of smallest to largest. Usually, in this case, even a person can sort it out without difficulty. However, the data mainly handled by the computer may be 10,000 or 10,000,000. And in the case of a database, theoretically, it should be able to handle an infinite number of data.
At this time, if the data is not sorted, you have to search by looking at the data one by one, but if the data is already sorted, you can use a powerful algorithm such as the binary search as an example above. (In fact, this is the main reason)
Let's take a look at the representative sorting algorithms, bubble sort, selection sort, insertion sort, merge sort, and quicksort.
Bubble sort

Bubble sort shows the worst performance in almost all situations, but it is the algorithm that shows the best performance because it only needs to traverse once for sorted data. You may be wondering why the already sorted data is sorted, but it is meaningful because the sorting algorithm itself operates without knowing whether the data is sorted or not.
Bubble sort works in the following order.
1.Sorting after comparing the 0th element with the 1st element
2.Sort the first and second elements after comparing them
…
3.Compare and sort the n-1th element with the nth element
Each traversal sorts the last one, so the elements appear to bubble up, so it's called bubble sort. The principle is intuitive, so it is easy to implement, but it is a fairly inefficient sorting method. So, usually when I first learn it, I rarely use it in practice after I write it.
Selection sort
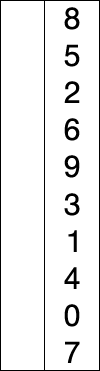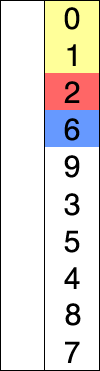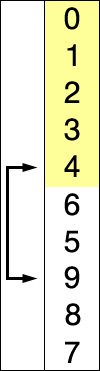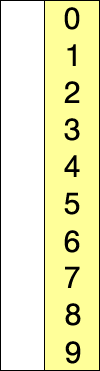
Selection sort is a sorting algorithm that exchanges positions by finding and selecting the data that matches the current position among the given data. Once the traversal is performed, the data with the smallest value among all the data in the algorithm is located at the 0th index, so from the next iteration, the traversal starts from the 1st index and repeats.
Selection sort works in the following order:
1.Find the smallest value among the 0th index ~ nth index and swap it with the 0th index
2.Find the smallest value among the 1st index ~ nth index and swap it with the 1st index
…
3.Find the smallest value among the n-1 index ~ n index and swap it with the nth index
Insertion sort
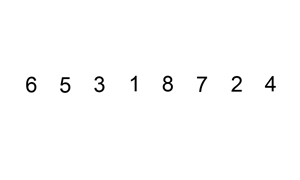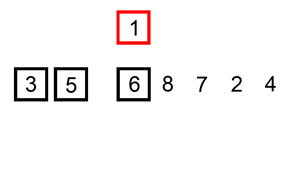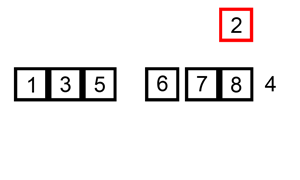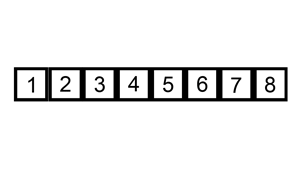
Insertion sort is a sort in which all elements of a given data are compared with the data parts sorted from the front in order, and their positions are found and inserted. In fact, the sort that can be said to be the most similar to the order in which humans directly sort, imagine that you are sorting the cards in your hand. Roughly speaking, you would do something like this:
1.Choose one card.
2.I look through the cards I have.
3.Put the cards in the order in which they are currently placed.
Insertion sort works similarly to this order.
1.Index 0 is skipped.
2.Find the position where the 1st index value should be entered among 0~1 indices and insert it
3.Find the position where the 2nd index value is to be entered among the 0~2 indexes and insert it.
…
4.Find the position where the nth index value should be entered among the 0~nth indices and insert it
In the best case, insertion sort has a time complexity of O(n)O(n) because it only needs to traverse the entire data once, but in the worst case it has a time complexity of O(n^2)O(n2).
References
1. https://en.wikipedia.org/wiki/Bubble_sort
2. https://en.wikipedia.org/wiki/Selection_sort
3. https://en.wikipedia.org/wiki/Insertion_sort
