[Algorithm] Tree

Tree concept

A tree is a data structure composed of nodes, and is a non-linear data structure, not a linear structure such as a stack or queue.

A tree is a data structure that represents a hierarchical relationship.

A tree has the following characteristics.

1. A tree has one root node.

2. A root node has zero or more child nodes.

3. Child nodes also have zero or more child nodes.

4. It is composed of nodes and edges connecting the nodes.

There cannot be cycles in a tree. Here, a cycle is said to exist if it can start from the starting node, go through other nodes, and then return to the starting node again.

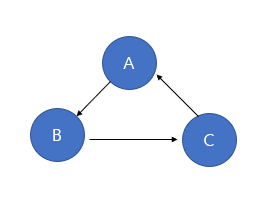
1. A tree can be said to be a connected graph without cycles.

2. Nodes in the tree must not have a self-loop
   

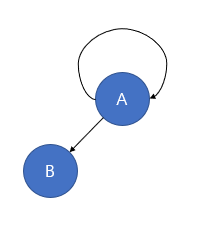
3. A tree with N nodes always has N-1 edges.

4. Every child node has only one parent node.

Terms related to trees.

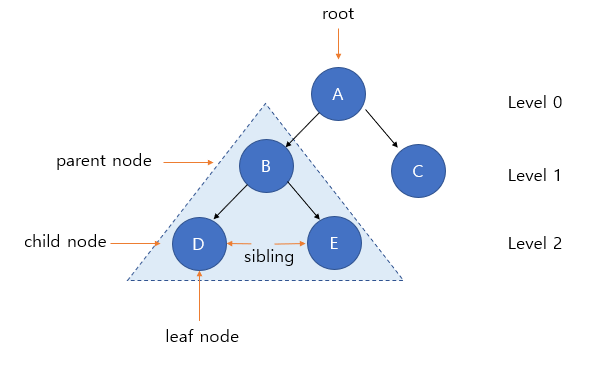
Root node: A node that has no parent, and the tree has only one root node. (ex: A-root node)

Leaf node: A node with no children is also called a terminal node. (ex: C, D, E - terminal node)

Internal node: A node that is not a terminal node (ex: A, B - internal node)

edge: line connecting nodes

Sibling: Nodes that have the same parent node (ex: D-E, B-C: Siblings)
Node depth: the number of edges that the root node must traverse to reach a certain node (ex: depth of D: 2)

Node level: a set of nodes with a specific depth in the tree ( ex : level 1- {B, C} )

Node degree: number of child nodes ( ex : B degree - 2, C degree - 0)

degree of tree: the maximum degree of the tree (ex: the degree of the tree above is 2)

Tree types

1. Binary Tree

A binary tree is a tree in which each node has at most two children. That is, each node has no children, one or only two children.

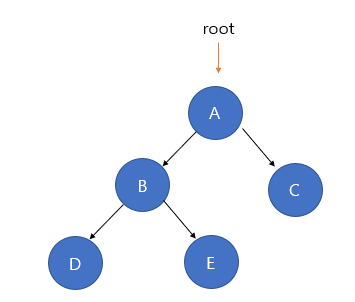
Binary trees can be searched through pre-order traversal, infix traversal, and post-order traversal.

2. Complete Tree, Full Binary Tree, Perfect Binary Tree

Complete Binary Tree

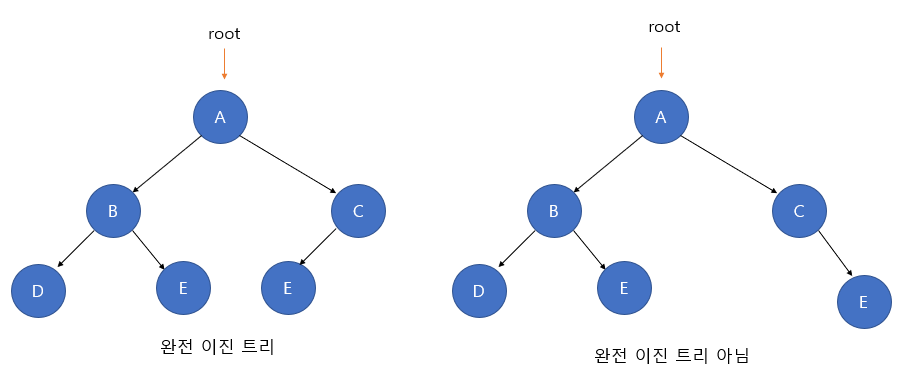
1) In a complete binary tree, all levels are completely filled except for the last level.

2) The last level does not have to be full, but the nodes must be filled from left to right.

3) You can have 1~2h-1 nodes in the last level h.

4) A complete binary tree can be efficiently expressed using an array.

Full Binary Tree

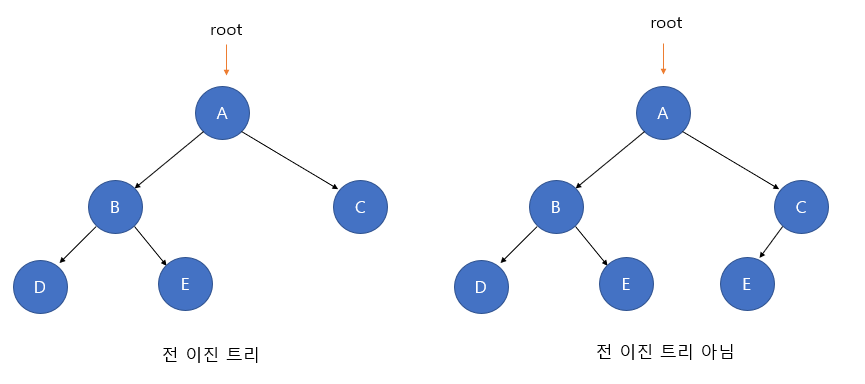
1) A full binary tree is a tree in which every node has either 0 or 2 child nodes.

Perfect Binary Tree

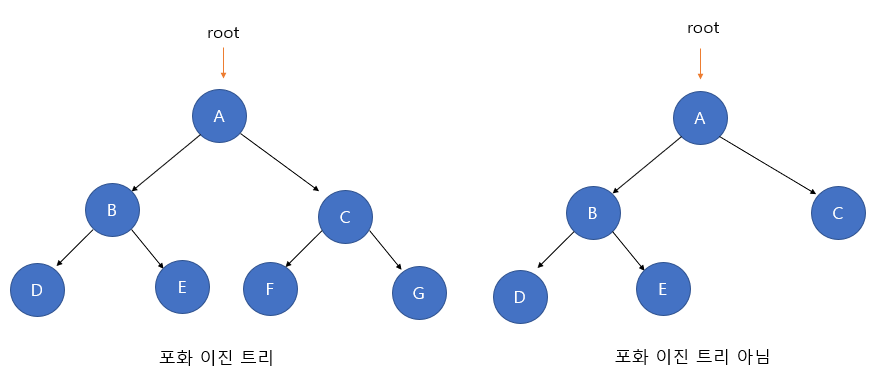
1) A saturated binary tree is a tree in which all levels are full of nodes.

2) The properties of the entire binary tree must also be satisfied. That is, every node has either 0 or 2 child nodes.

3) All end nodes have the same depth or level.

4) The number of nodes in the tree must be exactly 2^k-1. where k is the height of the tree.

3. Binary Search Tree

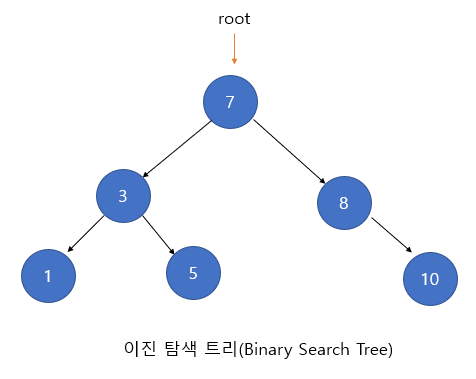
A binary search tree is a binary tree and a tree with the following properties.

1) A key stored in a node of a binary search tree is unique.

2) The height of the parent is greater than the height of the left child node.

3) The height of the parent is less than the height of the right child node.

4) The left and right subtrees are also binary search trees.

A binary search tree is a tree designed for efficient search.

If you want to learn more about binary search trees, see the next post.