⚡️ Time Complexity
Thinking about how to implement an efficient algorithm considering time complexity and
Let's see how to represent time complexity using Big-O notation.
❗️Efficient Algorithm Contemplation
When solving an algorithmic problem, it is most important to find a solution to the problem.
However, it is equally important that the problem is solved in an efficient way.
If you are trying to solve a problem and ask yourself, ‘Isn’t there a more efficient way than this?
Or is this the best way?'
Thinking about an efficient method is the same as thinking about time complexity.
Learn about time complexity and Big-O notation.
❗️Time complexity
What does it mean to consider time complexity when implementing the logic of an algorithm to solve a problem in code?
When implementing the logic of an algorithm in code, considering the time complexity is
It means ‘how much time does it take to execute an operation according to the change of the input value compared to the number of operations?’.
Implementing an efficient algorithm means constructing an algorithm that minimizes the rate of increase in time as the input value increases.
And this time complexity is mainly expressed using Big-O notation.
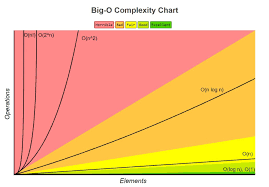
❗️Big-O notation
👉 How to express time complexity
Big-O ⇒ upper bound asymptote
Big-Ω (big-omega) ⇒ lower limit asymptote
Big-θ (big-theta) ⇒ the average of the two
The above three notations are methods of expressing the time complexity for the worst case, best case, and median (average) cases, respectively.
👉 What is the most frequently used notation?
This is because the big-O notation considers the worst case, so even the worst case time spent in the process of executing the program can be considered.
Rather than considering “it takes at least a certain amount of time” or “it takes this amount of time,” consider “it may take up to this amount of time” to respond appropriately.
👉 Time complexity best case
I've implemented an algorithm that takes 1 second in the best case, 1 minute on average, and 1 hour in the worst case to return a result, let's assume that we consider the best case.
If we run this algorithm 100 times, it will take 100 seconds in the best case.
If it actually took more than an hour, the question arises, 'Where did the problem come from?'
Since only the best case is considered, figuring out where the problem is occurring takes a lot of time because we have to figure out a lot of the logic.
👉 When considering the case of medium time complexity
What if we consider the time complexity of expecting the mean?
I thought it would take 100 minutes to run the algorithm 100 times, but if it takes more than 300 minutes due to several worst cases, I have the same concerns as considering the best case.
👉 Time complexity worst case
Although it is an extreme example, it is better to ‘prepare by considering the worst case’ rather than calculating the time in the hope that the worst case does not occur as above.
Therefore, Big-O notation is used more often than other notations.
Big-O notation is a method of expressing ‘how much time does it take to execute an operation according to the change of the input value compared to the number of operations?’.
👉 Kinds of Big-O Notation
O(1)
O(n)
O(log n)
O(n2)
O(2n)
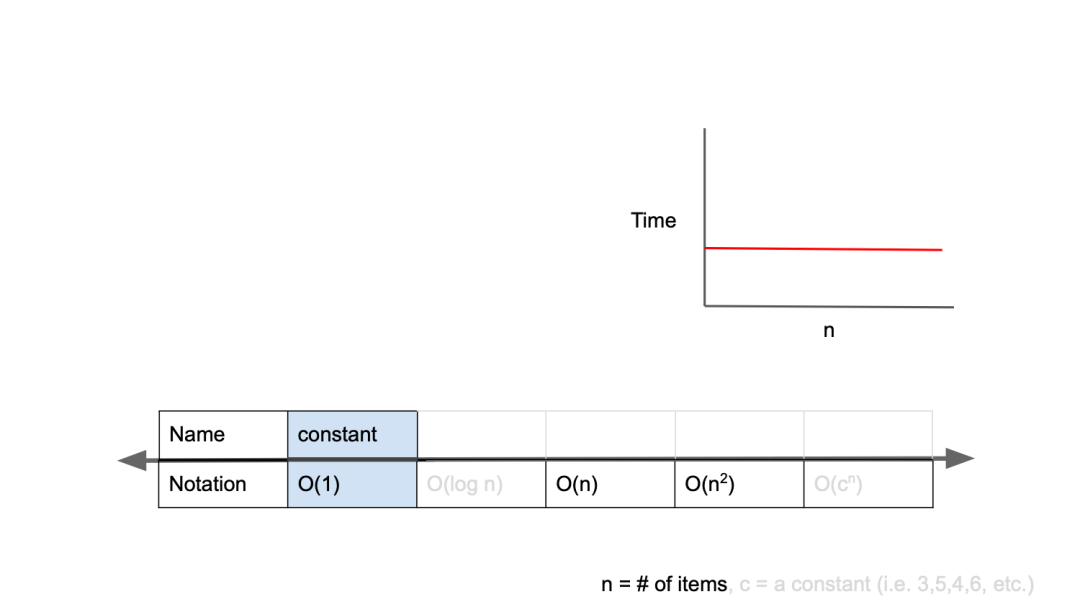
❗️O(1)
O(1) is called constant complexity, and the time does not increase even if the input value increases.
In other words, regardless of the size of the input value, the output value can be obtained immediately.
👉 Algorithms with time complexity of O(1)
function O_1_algorithm(arr, index) {
return arr[index];
}
let arr = [1, 2, 3, 4, 5];
let index = 1;
let result = O_1_algorithm(arr, index);
console.log(result); // 2
In this algorithm, no matter how large the input value becomes, the output value can be obtained immediately.
For example, even if the length of arr is 1 million, it is possible to immediately access the index and return a value.
❗️O(n)
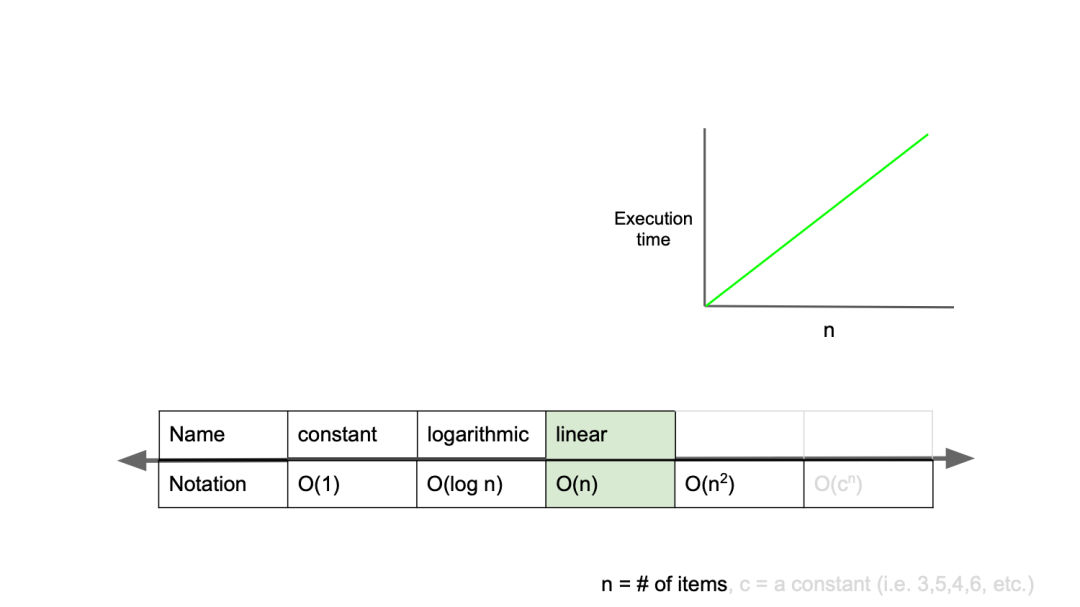
O(n) is called linear complexity, and it means that as the input value increases, the time also increases at the same rate.
For example, if an algorithm that takes 1 second when the input value is 1 and takes 100 seconds when the input value is increased by 100 times is 100 times 1 second, the algorithm can be said to have a time complexity of O(n). .
👉 Algorithms with time complexity of O(n)
function O_n_algorithm(n) {
for (let i = 0; i < n; i++) {
// do something for 1 second
}
}
function another_O_n_algorithm(n) {
for (let i = 0; i < 2n; i++) {
// do something for 1 second
}
}
In the O_n_algorithm function, whenever the input value (n) increases by 1, the execution time of the code increases by 1 second.
That is, as the input value increases, the time taken at the same rate increases. So what about the function another_O_n_algorithm ?
Whenever the input value increases by 1, the execution time of the code increases by 2 seconds.
Seeing this, he said, “Ah! Then I would say that this algorithm is O(2n)!” you can think
However, in fact, this algorithm is also written as O(n) in Big-O notation.
As the input value increases, the meaning (influence) of the coefficient (number in front of n) gradually fades.
❗️O(log n)
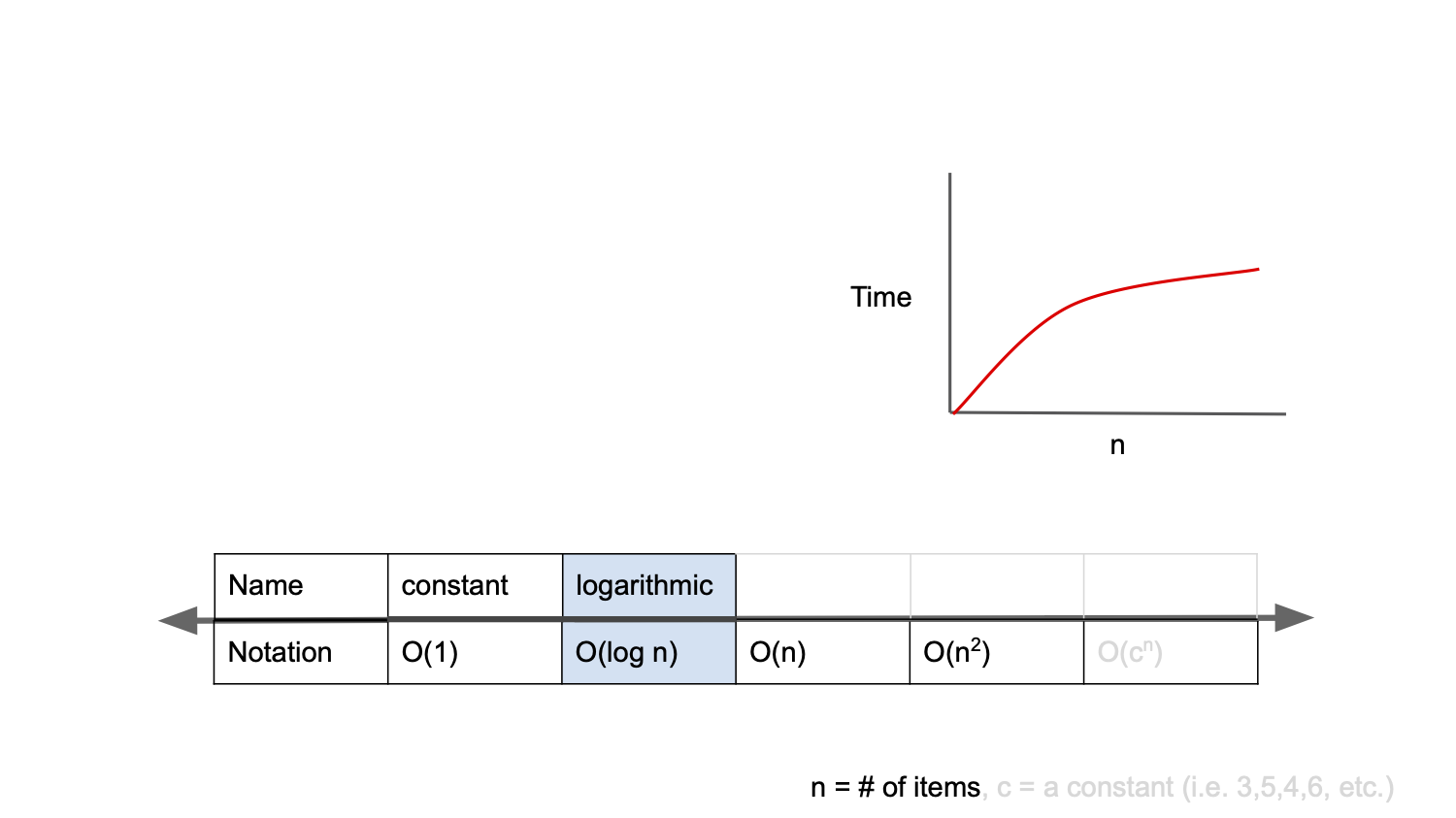
O(log n) is called logarithmic complexity, and it has the second fastest time complexity after O(1) in Big-O notation.
Remember the Binary Search Tree (BST) we learned about data structures?
In BST, when searching for a desired value, the number of cases is halved each time a node is moved.
An example of an easy-to-understand game is up & down.
Player 1 chooses a number from 1 to 100. (Assume you picked 30.)
If you present the number 50 (center), it is less than 50, so you shout down.
Since it is a number from 1 to 50, 25 is presented to reduce the number of cases by half again.
It is greater than 25, so shout up.
Continue to reduce the number of cases by half to find the correct answer.
Each time a number is presented, the number of cases is halved, so even in the worst case, it is possible to find the desired number in 7 times.
The value search of BST is also such a logic, and it is an algorithm (search technique) with a time complexity of O(log n).
❗️O(n2)
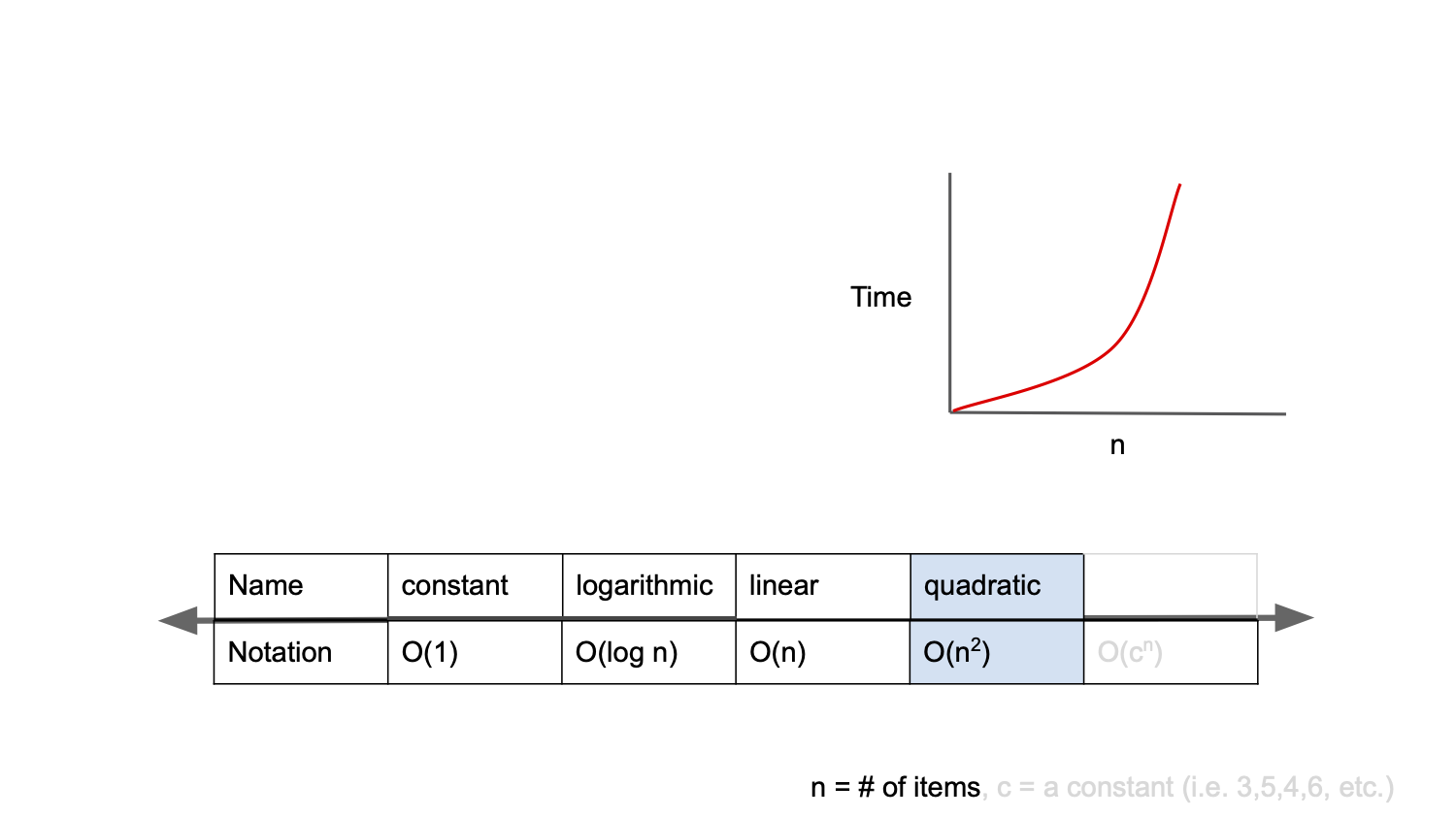
O(n2) is called quadratic complexity, and it means that the time increases as the number of squares of n as the input value increases.
For example, if the input value is 1, if a value of 5 is given to an algorithm that took 1 second, and it takes 25 seconds, the time complexity of this algorithm is expressed as O(n2).
👉 Algorithms with time complexity of O(n2)
function O_quadratic_algorithm(n) {
for (let i = 0; i < n; i++) {
for (let j = 0; j < n; j++) {
// do something for 1 second
}
}
}
function another_O_quadratic_algorithm(n) {
for (let i = 0; i < n; i++) {
for (let j = 0; j < n; j++) {
for (let k = 0; k < n; k++) {
// do something for 1 second
}
}
}
}
Just as both 2n and 5n are expressed as O(n), both n3 and n5 are expressed as O(n2).
This is indicated because the influence of the index gradually fades as n increases.
