백준_1495_기타리스트

기타리스트

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class Main {

    static int N, S, M;
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());

        N = Integer.parseInt(st.nextToken()); // 곡의 갯수
        S = Integer.parseInt(st.nextToken()); // 처음 볼륨
        M = Integer.parseInt(st.nextToken()); // 최대 볼륨

        st = new StringTokenizer(br.readLine());

        // 각 곡의 볼륨 변화 (N+1 크기로 선언)
        int[] V = new int[N + 1];

        for (int i = 1; i <= N; i++) {  // i는 1부터 시작
            V[i] = Integer.parseInt(st.nextToken());
        }

        // dp[i][j] : i번째 곡까지 연주했을 때 볼륨이 j인 경우 가능 여부 (true: 가능, false: 불가능)
        boolean[][] dp = new boolean[N + 1][M + 1];
        dp[0][S] = true; // 초기 볼륨으로 시작

		// 이전 값을 보고 현재 가능한 경우의 수 처리!
        for (int i = 1; i <= N; i++) {
            for (int j = 0; j <= M; j++) {
                if (dp[i - 1][j]) {
                    if (j + V[i] <= M) {
                        dp[i][j + V[i]] = true;
                    }
                    if (j - V[i] >= 0) {
                        dp[i][j - V[i]] = true;
                    }
                }
            }
        }

        // 마지막 곡까지 연주했을 때 가능한 최대 볼륨 찾기
        int maxVolume = -1;
        for (int i = M; i >= 0; i--) {
            if (dp[N][i]) {
                maxVolume = i;
                break;
            }
        }
        System.out.println(maxVolume);
    }
}

N = 3 (곡의 개수)
S = 5 (시작 볼륨)
M = 10 (최대 볼륨)
볼륨 변화량 = [5, 3, 7]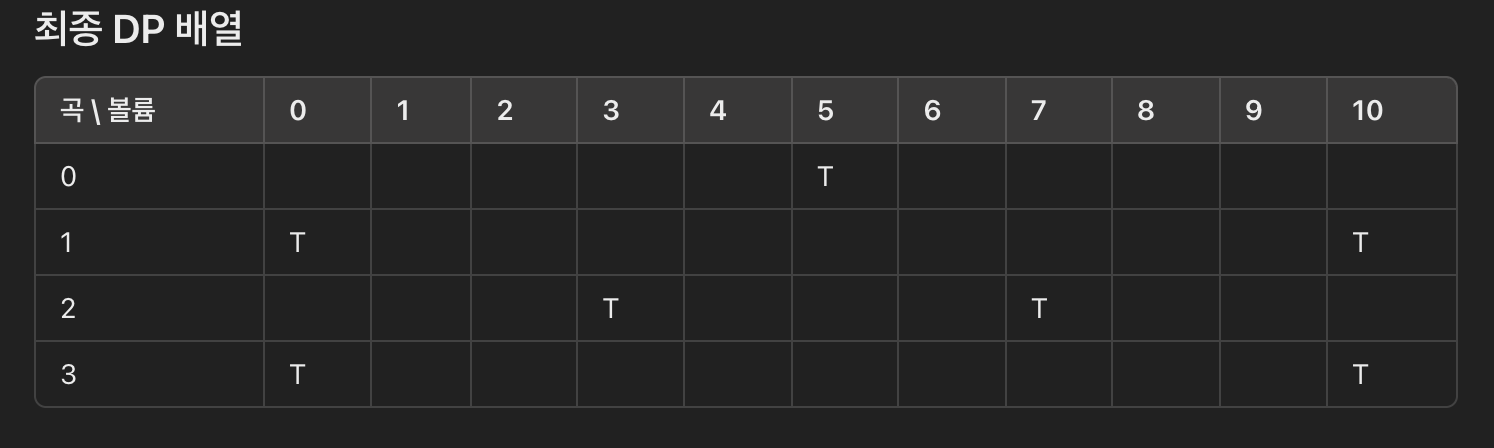

dp 테이블을 채우는 방식 차이

 for (int i = 1; i <= N; i++) {
            for (int j = 0; j <= M; j++) {
                if (dp[i - 1][j]) {
                    if (j + V[i] <= M) {
                        dp[i][j + V[i]] = true;
                    }
                    if (j - V[i] >= 0) {
                        dp[i][j - V[i]] = true;
                    }
                }
            }
        }

이전 곡(i-1)에서 현재 볼륨 j를 만들 수 있는지(dp[i-1][j])를 확인하고, 현재 곡(i)에서 볼륨 변화량 V[i]를 더하거나 빼서 새로운 볼륨을 만듬

• 이 방식은 이전 상태(i-1)에서 현재 상태(i)로 볼륨을 업데이트하는 접근 방식

for (int i = 1; i <= N; i++) {
            for (int j = 0; j <= M; j++) {
                // 볼륨 줄이기 (-)
                if (j - V[i] >= 0 && dp[i - 1][j - V[i]]) {
                    dp[i][j] = true;
                }
                // 볼륨 올리기 (-)
                if (j + V[i] <= M && dp[i - 1][j + V[i]]) {
                    dp[i][j] = true;
                }
            }
        }

현재 볼륨 j를 만들기 위해 이전 곡(i-1)에서 가능한 모든 경우를 체크

• 이 방식은 현재 상태(i)에서 이전 상태(i-1)를 참고하여 볼륨을 업데이트하는 접근 방식

차이점

업데이트 시점

• 첫 번째 방식: 이전 상태(i-1)에서 가능한 모든 볼륨을 확인하고, 현재 상태(i)의 볼륨을 업데이트
• 두 번째 방식: 현재 상태(i)의 볼륨을 만들기 위해 이전 상태(i-1)에서 가능한 모든 경우를 체크

루프 구조

• 첫 번째 방식: 이전 상태의 볼륨을 기반으로 현재 상태의 새로운 볼륨을 직접 업데이트.
• 두 번째 방식: 현재 상태의 볼륨을 만들기 위해 이전 상태의 볼륨을 역으로 추적하여 업데이트.

🤔 뭐가 더 좋을까?

• 첫 번째 방식
  내부 루프에서 조건문을 통해 볼륨을 더하고 빼는 경우를 따로 체크
  dp[i - 1][j]가 true인 경우에만 업데이트하므로, 불필요한 연산이 줄어듬

• 두 번째 방식
  모든 볼륨 범위에서 이전 곡의 볼륨을 줄이거나 늘리는 경우를 체크
  모든 경우를 다 체크하므로, 경우에 따라 더 많은 연산이 필요할 수 있음

👉 첫 번째 방식이 더 나은 선택일 가능성이 크다!