핵심키워드

• 가설함수(Hypothesis Function)
• 평균제곱오차(Mean Squared Error)
• 경사하강법(Gradient Descent)

Hypothesis Function 복습

bias가 없는 모델은 실제에서는 사용할 일 없지만, 오늘은 간단한 예제를 사용하기 위해

사용할 모의 data 확인

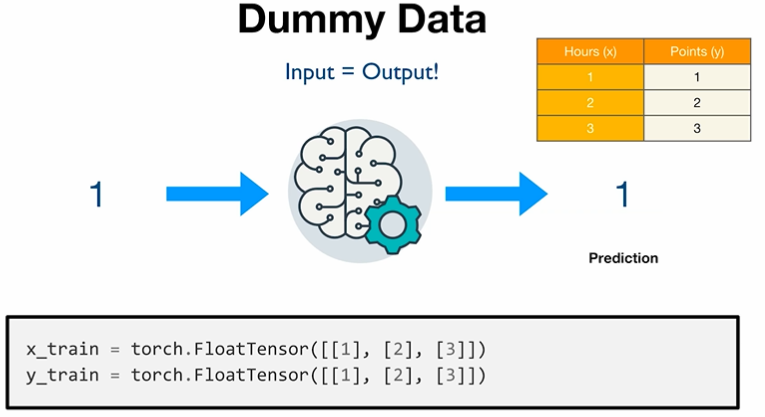
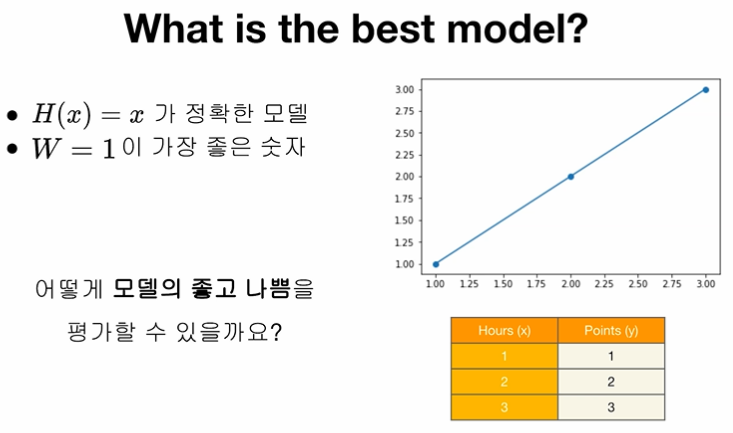최적의 모델일 때는 위와 같은 형태이겠지!

Cost Function 이해

cost function은 나의 예측값이 얼마나 정확한지 나타내주는 지표
잘 예측할 수록 값이 작을 것!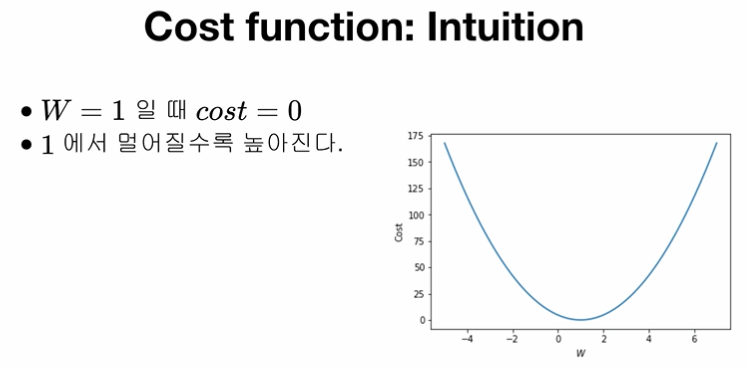 우리의 예제에서는 W=1일 때 완벽하게 예측했으므로
보통 cost function은 MSE를 많이 이용

Gradient Descent 이론

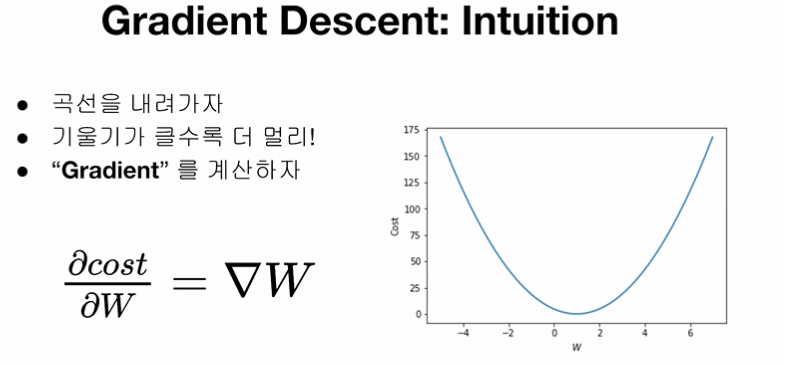cost function의 값을 최소화하는 것이 우리의 목표!
따라서 위의 그래프에서 기울기가 음수일 때는 W가 더 커져야 하고, 기울기가 양수일 때는 W가 더 작아져야 함
또한, 기울기가 가파를수록 cost가 큰 것이니 W를 많이 바꾸고, 기울기가 평평할수록 cost가 작은 것이니 W를 살짝 바꿔야 함
=> 이 기울기를 Gradient라고 함
cost function이 2차함수이기 때문에 우리는 미분을 통해 gradient를 구할 수 있음
=> gradient를 이용해서 cost를 줄이기

Gradient Descent 구현

gradient를 직접 구현한 코드

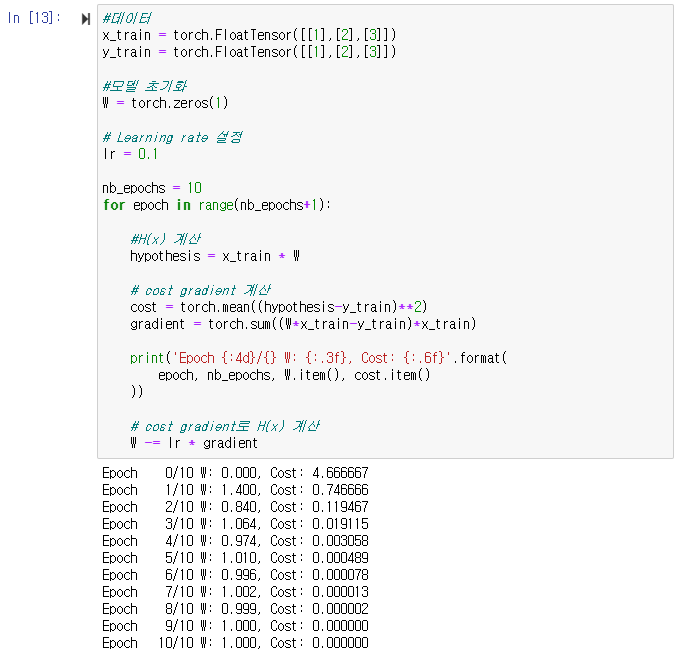
실제로 코드를 짤 때 위처럼 쓸 일 없음

optim을 이용한 코드

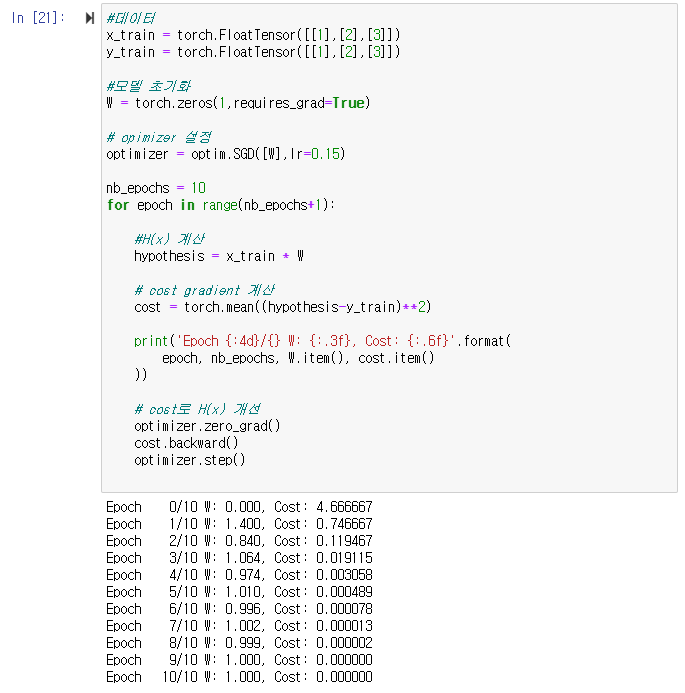당연히 W=1에 수렴하고 cost는 감소하는 것을 볼 수 있음 :D

이제 우리는 단일선형회귀가 아닌 다항선형회귀를 공부하러~