Polygon Mesh - 에지 검색 테이블

폴리곤 메시를 가공하거나 화면에 가시화하려는 목적으로 프로그램 내부에서 다루는 표현형(representation)엔 여러 방법이 있을 수 있는데, 그 중 대표적인 두 가지는 다음과 같다.

• 좌 삼각형의 세 정점 좌표를 죽 나열하는 방식 (triangle soup)
• 우 정점 리스트와, 세 정점 인덱스로 면(face)을 표현하는 방식 (indexed triangles)

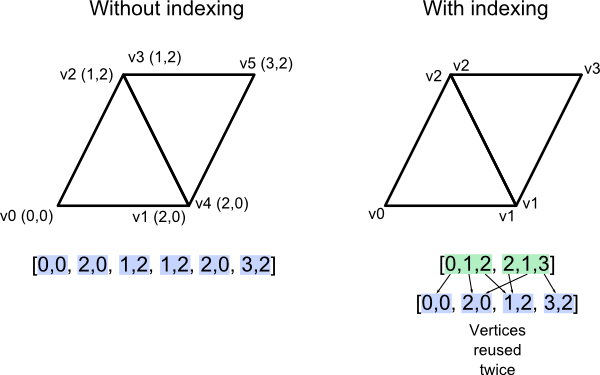
각 방식의 장단점은 기회가 되면 따로 논해보고..., 데이터 처리를 위한 목적으로는 첫 번째 표현형은 사용하기 어려우므로, 이제부터는 두 번째 표현형만을 대상으로 논해보겠다.

아래처럼 좀 단순한, 7개의 정점(vertex)과 4개의 면(face)으로 이루어진 삼각망을 생각해보자.

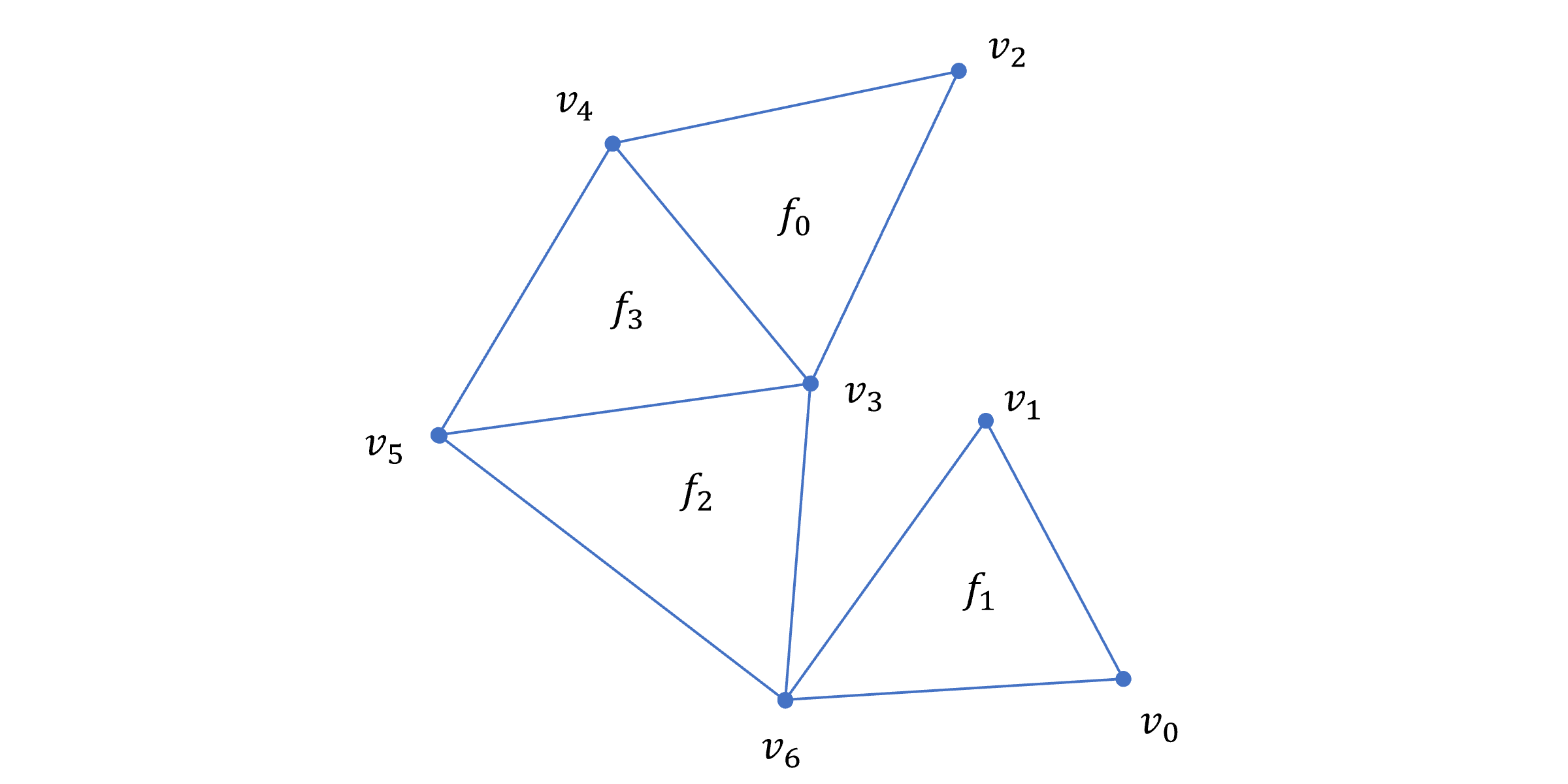
이 때 삼각형 리스트는 아래처럼 표현될 수 있을 것이다. (fn , vn 등에서 첨자만을 표기)

face index	0	1	2	3
vertex indices	4, 3, 2	1, 6, 0	3, 5, 6	4, 5, 3

C++ 소스코드로 나타내면 아래 정도...

struct Face { int vertices[3]; };

std::vector<Face> faces = { { 4, 3, 2 }, { 1, 6, 0 }, { 3, 5, 6 }, { 4, 5, 3 } };

이 글에서는 이러한 indexed triangle 리스트(face list)로부터 아래 초록색으로 표시된 edge를 구성하는 정점 목록을 만들고 순회하는 방법을 공유해보려 한다.

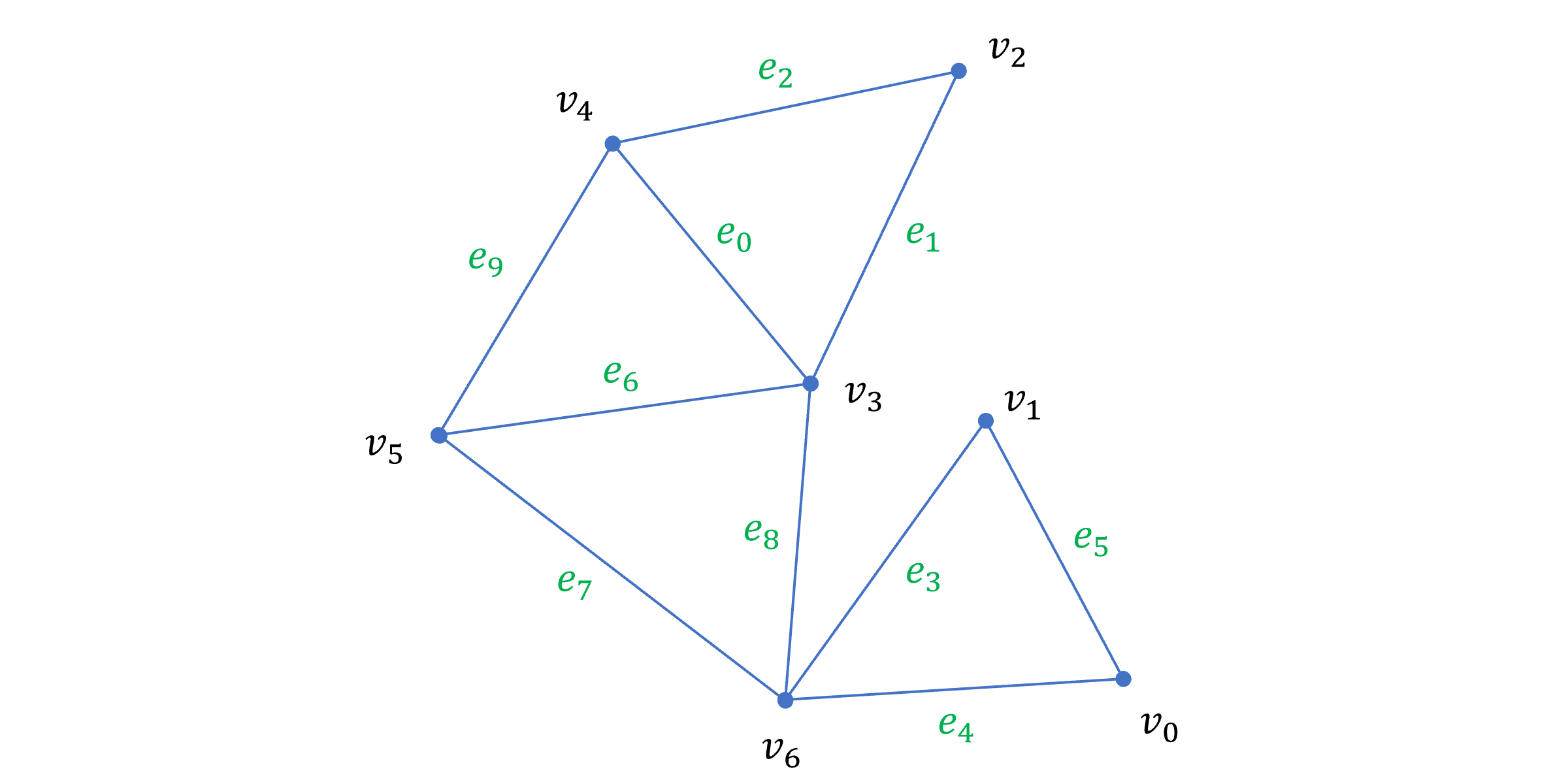
edge index	0	1	2	3	4	5	6	7	8	9
vertex indices	3, 4	2, 3	2, 4	1, 6	0, 6	0, 1	3, 5	5, 6	3, 6	4, 5

Mesh의 위상을 관리하는 자료구조에 따라 Edge를 explicit하게 포함할 수도 있다. 아래와 같은 half-edge 기반의 mesh representation이 대표적이다...

• https://www.graphics.rwth-aachen.de/software/openmesh/
• https://jerryyin.info/geometry-processing-algorithms/half-edge/

Half-edge 기반 mesh representation은 메시를 다루기 위해 가장 널리 사용되는 자료구조이지만, 메모리 단편화가 심하고, 메모리 사용량이 많고, representation 생성에 소요되는 비용이 크다는 문제가 있다. 이런 이유에서 최소한의 vertex array, face array 를 주 자료구조로만 사용하고 위상을 관리하는 topology table은 필요할 때에만 생성하는 방식을 개인적으로 선호한다.
본 문서에서 소개하는 Edge Table은 vertex array, face array 로부터 edge 목록을 만들고 순회할 수 있는 해 주는 알려진 가장 빠르고 가벼운 자료구조이며, "필요할 때에만 생성"해서 "쓰고 난 후 부담없이 버리"는 데이터 관리 방식에 적합하다.

---

1. std::set 사용하기

아래처럼 Edge 클래스를 만들고 strict weak ordering을 만족하는 operator<를 정의하면 쉽게 std::set 또는 std::map의 키로 사용할 수 있다.

• 순서가 반대인 것들도 equivalent 하도록 취급하기 위해 오름차순 정렬된 묶음인 oriented() 함수를 정의해서 비교함.
• 오버헤드 없이 간단하게 lexicographic compare 를 구현하기 위해 std::tie를 사용함.
  • Simplifying lexicographical comparisons with C++
  • What's the simplest way of defining lexicographic comparison for elements of a class?

struct Edge {
    int vertices[2];

    auto& lo() const noexcept { return vertices[vertices[0] >= vertices[1]]; }
    auto& hi() const noexcept { return vertices[vertices[0] < vertices[1]]; }
    auto oriented() const noexcept { return std::tie(lo(), hi()); }
    bool operator<(const Edge& rhs) const noexcept { return oriented() < rhs.oriented(); }
};

int main() {
    std::set<Edge> edges;

    for (auto& face : faces) {
        edges.insert({ face[0], face[1] });
        edges.insert({ face[1], face[2] });
        edges.insert({ face[2], face[0] });
    }
}

위 예제의 edges.insert({ face[0], face[1] }); 을 가능하게 하려면 operator[]를 오버로딩할 필요가 있다.

struct Face {
    int vertices[3];

    int& operator[](size_t n) { return vertices[n]; }
    int operator[](size_t n) const { return vertices[n]; }
};

online example

• https://www.online-cpp.com/LvRHT0F9nr

2. std::unordered_set 사용하기

아래처럼 std::hash와 std::equal_to 클래스를 Edge 클래스에 대해 특화(specialization) 하면 unordered associative container의 키로 사용할 수 있다.

template <> struct std::hash<Edge> {
    std::size_t operator()(const Edge& edge) const noexcept {
        return edge.lo() ^ (edge.hi() << 1);
    }
};

template <> struct std::equal_to<Edge> {
    bool operator()(const Edge& lhs, const Edge& rhs) const noexcept {
        return lhs.oriented() == rhs.oriented();
    }
};

삼각망에서 정점 주변의 에지는 평균적으로 6개 전후이므로, 아래처럼 hash function을 보다 단순하게 가져가도 collision 처리를 위한 비용은 그리 크지 않다.

template <> struct std::hash<Edge> {
    std::size_t operator()(const Edge& edge) const noexcept {
        return edge.lo();
    }
};

std::equal_to<Edge>를 특화하는 대신 operator== 연산자를 오버로딩하는 것도 물론 가능하다.

  struct Edge {
      // 중략
      bool operator==(const Edge& rhs) const noexcept { return oriented() == rhs.oriented(); }
  };

online example

• https://www.online-cpp.com/loRIqSjkaQ

3. 전용 Edge Table을 사용하기

std::set과 std::unordered_set은 자료구조가 가진 태생적인 한계가 있다.

• 좋지 못한 시간복잡도 std::set은 $O(n\log n)$ 시간복잡도를 갖는다.
• 메모리 할당 비용 및 단편화 std::unordered_set의 경우 open-source 대체제가 존재하긴 한다.
• 느린 검색 성능 이진 탐색, 또는 해싱에 소요되는 비용 때문에 오버헤드를 감수해야 한다.

이런 한계 없이 최고의 성능을 내고자 한다면 직접 구현하는 수 밖에 없다. 내가 Edge Table을 만들 때 사용하는 방법을 소개할까 한다.

3.1 Singly linked list를 사용하는 버전

먼저, Edge를 구성하는 두 정점 중 더 작은 값을 공유하는 단일연결리스트(singly linked list)를 생각해 보자. 이 방법은 unordered_set 구현과 논리적으로 사실상 동일하다고 할 수 있다.

class EdgeTable {
    struct Node {
        int hi = -1;
        Node* next = nullptr;
    };
    
    std::vector<Node*> nexts_;
};

이 자료구조에 임의의 Edge를 삽입하는 동작을 구현하면 아래 정도가 되겠다.

    void EdgeTable::insert(const Edge& e) {
        // 에지의 작은 버텍스 인덱스(e.lo())에 접근할 수 없다면 벡터 크기를 키움
        if (nexts_.size() <= size_t(e.lo())) {
            nexts_.resize(e.lo() + 1, nullptr);
        }

        // 중복 에지를 발견하면 종료
        for (auto next = nexts_[e.lo()]; next; next = next->next) {
            if (next->hi == e.hi()) {
                return;
            }
        }

        // 큰 버텍스 인덱스(e.hi())를 단일연결리스트에 추가
        nexts_[e.lo()] = new Node{ e.hi(), nexts_[e.lo()] };
    }

전체 테이블은 아래 함수를 통해 순회할 수 있고.

    void EdgeTable::for_each(std::function<void(const Edge&)> visitor) {
        for (int lo = 0; lo != nexts_.size(); ++lo) {
            for (auto next = nexts_[lo]; next; next = next->next) {
                visitor(Edge{ lo, next->hi });
            }
        }
    }

online example

• https://www.online-cpp.com/iwBNC1b4dm

3.2 Singly linked list - array implementation

연결리스트는 아무래도 메모리 할당 오버헤드와 단편화 문제에서 자유로울 수 없다. 연결리스트의 노드는 고정된 크기를 가지므로 다양한 형태의 고정크기 할당자(fixed allocator)를 도입해서 문제를 해결할 수도 있을 테지만 여기서는 보다 단순한 방법을 설명해보겠다.

먼저, 노드의 정의를 아래처럼 변경하고, 두 개의 배열을 준비한다. 첫 번째는 lo-index 배열, 두 번째는 노드의 배열.

class EdgeTable {
    struct Node {
        int hi = -1;
        int next = -1;
    };

    std::vector<int> nexts_;
    std::vector<Node> nodes_;
};

임의의 Edge를 삽입할 때 아래의 방식으로 테이블을 만들어나가면 된다.

• 첫 번째 배열의 lo-index 위치에 두 번째 배열의 위치 A를 가리키도록 (-1은 무효)
• 두 번째 배열의 위치 A::vertex는 hi-index, A::next는 두 번째 배열의 다음 위치.
• A::next == -1 이라면 연결리스트의 끝.

    void EdgeTable::insert(const Edge& e) {
        // 에지의 작은 버텍스 인덱스(e.lo())에 접근할 수 없다면 벡터 크기를 키움
        if (nexts_.size() <= size_t(e.lo())) {
            nexts_.resize(e.lo() + 1, -1);
        }

        // 중복 에지를 발견하면 종료
        for (auto next = nexts_[e.lo()]; next > -1; next = nodes_[next].next) {
            if (nodes_[next].hi == e.hi()) {
                return;
            }
        }

        // 큰 버텍스 인덱스(e.hi())를 노드 배열 마지막에 추가하고, 첫번째 배열을 갱신
        nodes_.push_back(Node{ e.hi(), nexts_[e.lo()] });
        nexts_[e.lo()] = int(nodes_.size() - 1);
    }

앞서 포인터를 사용한 버전의 예제와 골격이 거의 다르지 않은데, new Node{...}가 사라지고 메모리 할당은 nexts_.resize()와 nodes_.push_back() 내부에서 수행되는 차이는 쉽게 확인할 수 있을 것이다.

전체 테이블을 순회하는 함수도 포인터 버전과 대동소이하게 구현할 수 있다.

    void EdgeTable::for_each(std::function<void(const Edge&)> visitor) {
        for (int lo = 0; lo != nexts_.size(); ++lo) {
            auto next = nexts_[lo];
            while (next > -1) {
                visitor(Edge{ lo, nodes_[next].hi });
                next = nodes_[next].next;
            }
        }
    }

online example

• https://www.online-cpp.com/PxkUBYdupy

마무리

삼각망으로부터 EdgeTable 이라는 자료구조를 생성하고 순회하는것 만을 설명했지만 조금만 응용하면 아래와 같은 동작들도 쉽게 구현할 수 있다.

• 임의의 Edge가 EdgeTable에 존재하는 지 여부를 검사
• 임의의 Edge에 unique한 id.를 부여
• EdgeTable로부터 array of Edge 를 생성
• ...

그리고, 이 방법은 pointer를 지원하지 않는 Python, JavaScript 등에서도 유효하다!