Polyline Simplification

1. Douglas-Peucker algorithm

가장 유명한 폴리라인 단순화 알고리즘. 다른 이름은 Ramer-Douglas-Peucker 알고리즘이지만, 내 경험상 D-P법이라 부르는 사람들이 많았다.

• https://en.wikipedia.org/wiki/Ramer-Douglas-Peucker_algorithm

아래 그림에 보이듯, 양 끝점을 잇는 직선에서 가장 먼 거리에 위치한 점을 찾아 새로운 양 끝점을 취해 다시 recursive 하게 가장 먼 거리를 찾아 나가는 방식이다. 전형적인 분할정복(divide and conquer) 알고리즘이고, 따라서 time complexity 역시 $O(n \log n)$ 근처가 된다.

• best-case: $O(n \log n)$ (e.g. convex hull)
• worst-case: $O(n^2)$ (e.g. 가장 먼 거리의 점이 양 끝점 바로 옆에 위치하는 경우)

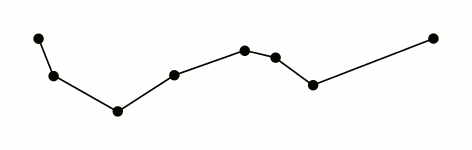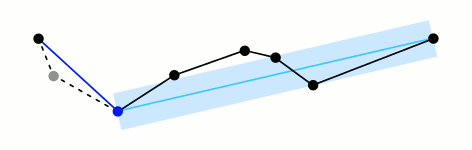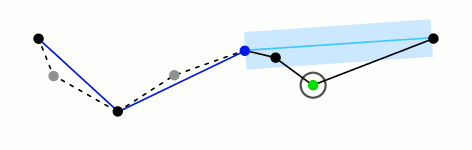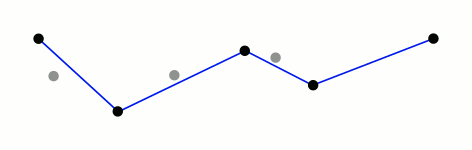
위 Wikipedia 링크를 보면 아래 커브를 예로 들고 있는데, 테스트하기에 적당한 샘플이라 생각되어 이 문서에서도 이를 대상으로 코드를 작성해 보겠다.

curve equation	simplification results
$f(x) = e^{-x} \cos(2 \pi x)$

1.1 sample polyline 생성하기

먼저 위 커브 $f(x) = e^{-x} \cos(2 \pi x)$ 꼴의 polyline을 생성하는 코드는 대략 아래와 같다.

struct Vector2 {
    double x;
    double y;
};

auto generatePolyline(double from = 0.0, double to = 5.0, size_t division = 100) {
    std::vector<Vector2> polyline;
    polyline.reserve(division + 1);
    
    for (size_t i = 0; i <= division; ++i)     {
        auto t = double(i) / division;
        auto x = from * (1 - t) + to * t;

        polyline.push_back(Vector2{ x, std::exp(-x) * cos(x * 2 * M_PI) });
    }

    return polyline;
}

1.2 직선과 점 사이의 거리 계산

두 개의 점을 잇는 직선으로부터 임의의 좌표 까지의 거리(deviation)를 계산하기 위해 Vector2 클래스에 유틸리티성 메쏘드를 추가하자.

struct Vector2 {
    double x;
    double y;

    auto length2() const { return x * x + y * y; }
    auto distance2(const Vector2& v) const { return (x - v.x) * (x - v.x) + (y - v.y) * (y - v.y); }
    auto dot(const Vector2& rhs) const { return x * rhs.x + y * rhs.y; }
    auto cross(const Vector2& rhs) const { return x * rhs.y - y * rhs.x; }
    auto operator*(double scale) const { return Vector2{ x * scale, y * scale }; }
    auto operator+(const Vector2& rhs) const { return Vector2{ x + rhs.x, y + rhs.y }; }
    auto operator-(const Vector2& rhs) const { return Vector2{ x - rhs.x, y - rhs.y }; }

    auto lineDistance2(const Vector2& p0, const Vector2& p1) const     {
        auto diff = p1 - p0;
	    auto length2 = diff.length2();

	    auto t = (length2 > 0) ? (diff.dot(p - p0) / length2) : 0.0;
	    t = std::max(0.0, std::min(1.0, t));

	    return p.distance2(p0 * (1 - t) + p1 * t);
    }
};

online example

• https://www.online-cpp.com/nElqtfix4z

1.3 폴리라인 단순화

재귀호출 시 vector<bool>& select 인자를 넘겨 남겨질 놈들을 마킹하는 방식을 취했다.

void simplifyPolyline_(const std::vector<Vector2>& polyline,
    std::vector<bool>& select, size_t first, size_t last, double tol2) {
    auto split = last;
    auto max_dist2 = 0.0;
    
    for (auto i = first + 1; i + 1 < last; ++i)     {
        auto dist2 = polyline[i].lineDistance2(polyline[first], polyline[last]);
        if (max_dist2 < dist2) {
            split = i, max_dist2 = dist2;
        }
    }

    if ((split < last) && (tol2 <= max_dist2)) {
        select[split] = true;

        simplifyPolyline_(polyline, select, first, split, tol2);
        simplifyPolyline_(polyline, select, split, last, tol2);
    }
}

auto simplifiedPolyline(const std::vector<Vector2>& polyline, double tol)
{
    std::vector<Vector2> simplified;

    if (!polyline.empty()) {
        std::vector<bool> select(polyline.size(), false);
        select.front() = select.back() = true;

        simplifyPolyline_(polyline, select, 0, polyline.size() - 1, tol * tol);

        for (size_t i = 0; i != polyline.size(); ++i) {
            if (select[i]) {
                simplified.push_back(polyline[i]);
            }
        }
    }

    return simplified;
}

online example

• https://www.online-cpp.com/84UCnobIai

2. 에지 길이를 고려한 폴리라인 단순화

실제로 사용하다보면 폴리라인 원본과 단순화된 형상과의 편차(deviation)만을 판단하게 되므로 의도와는 다르게 지나치게 긴 세그먼트가 생성될 수도 있다.
아래는 일정 길이 이상의 세그먼트가 생성될 경우 편차의 크기와는 관계 없이 subdivision을 수행하도록 수정한 버전이다.

void simplifyPolyline_(const std::vector<Vector2>& polyline,
    std::vector<bool>& select, size_t first, size_t last, double tol2, double maxLength2) {
    auto split = last;
    auto max_dist2 = 0.0;
    
    for (auto i = first + 1; i + 1 < last; ++i)     {
        auto dist2 = polyline[i].lineDistance2(polyline[first], polyline[last]);
        if (max_dist2 < dist2) {
            split = i, max_dist2 = dist2;
        }
    }

	auto do_split = (tol2 <= max_dist2) ||
    	(maxLength2 < polyline[first].distance2(polyline[last]);

    if ((split < last) && do_split) {
        select[split] = true;

        simplifyPolyline_(polyline, select, first, split, tol2);
        simplifyPolyline_(polyline, select, split, last, tol2);
    }
}

끝.