[TIL] HTTP : The Definitive Guide "p315 ~ p317"

시윤·2025년 4월 13일

TIL http

[TIL] Two Pages Per Day

목록 보기

127/146

Chapter 14. Secure HTTP

(해석 또는 이해가 잘못된 부분이 있다면 댓글로 편하게 알려주세요.)

✏️ 원문 번역

Public-Key Cryptography

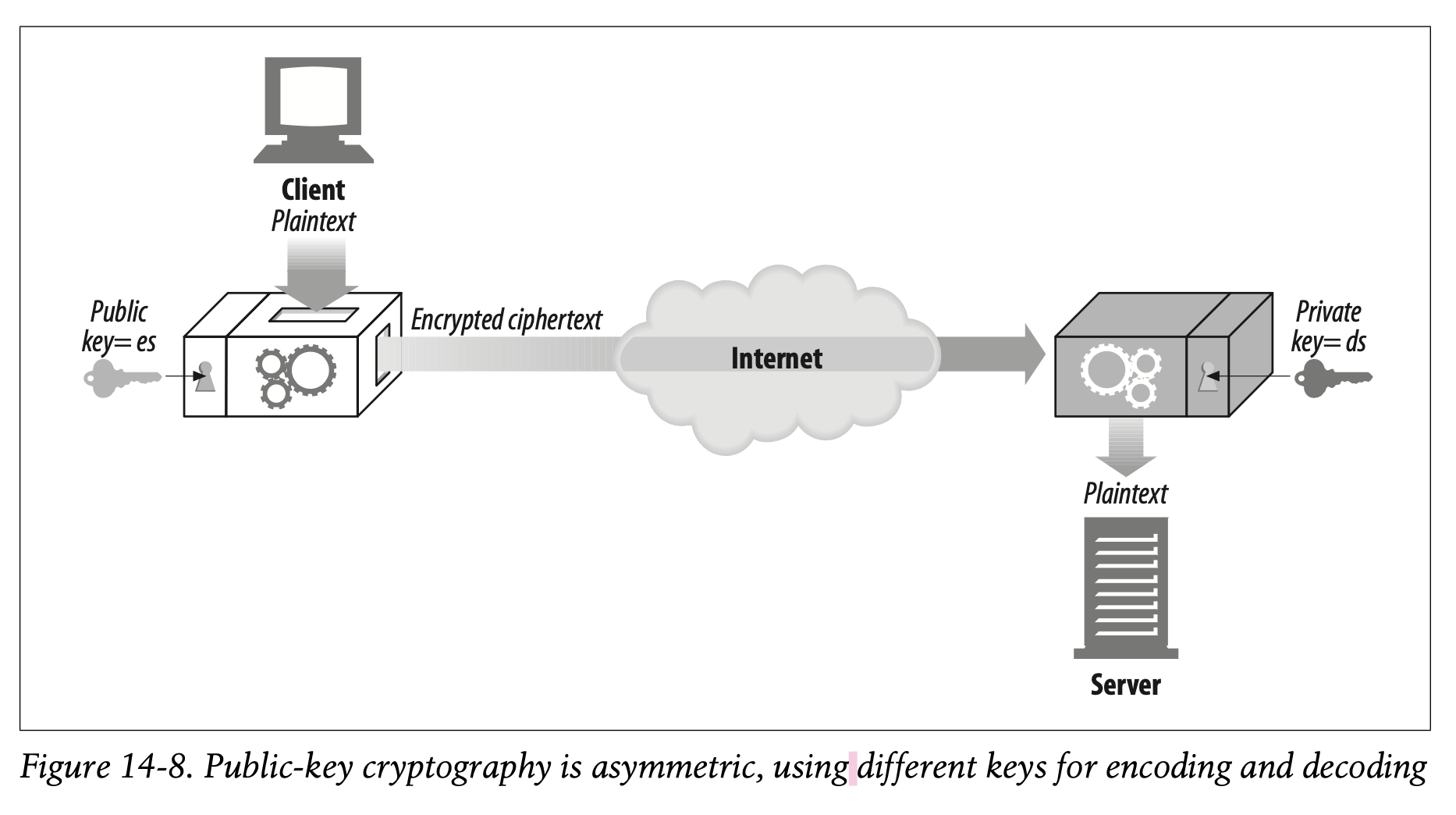
Instead of a single encoding/decoding key for every pair of hosts, public-key cryptography uses two asymmetric keys: one for encoding messages for a host, and another for decoding the host’s messages. The encoding key is publicly known to the world (thus the name public-key cryptography), but only the host knows the private decoding key (see Figure 14-8). This makes key establishment much easier, because everyone can find the public key for a particular host. But the decoding key is kept secret, so only the recipient can decode messages sent to it.

Public-Key Cryptography는 모든 호스트 쌍에 대해 하나의 인코딩/디코딩 키를 사용하는 대신 두 개의 비대칭 키를 활용합니다.
한 키는 호스트가 메시지를 암호화하는 데 사용되며, 다른 하나는 호스트의 메시지를 복호화하는 데 사용됩니다.
인코딩 키는 공개적으로 알려져 있습니다. 해당 암호화 기법을 Public-Key Cryptography라고 부르는 이유기도 합니다.
하지만 비공개 디코딩 키는 오직 호스트만이 알고 있습니다. (Figure 14-8)
이 방식은 모든 사람이 특정 호스트에 대한 Public Key를 알 수 있기 때문에 키 설정 과정을 훨씬 간소화할 수 있습니다.
그러나 디코딩 키는 반드시 유출되지 않아야 합니다. 오직 수신자만이 전송 받은 메시지를 해독할 수 있어야 하기 때문입니다.

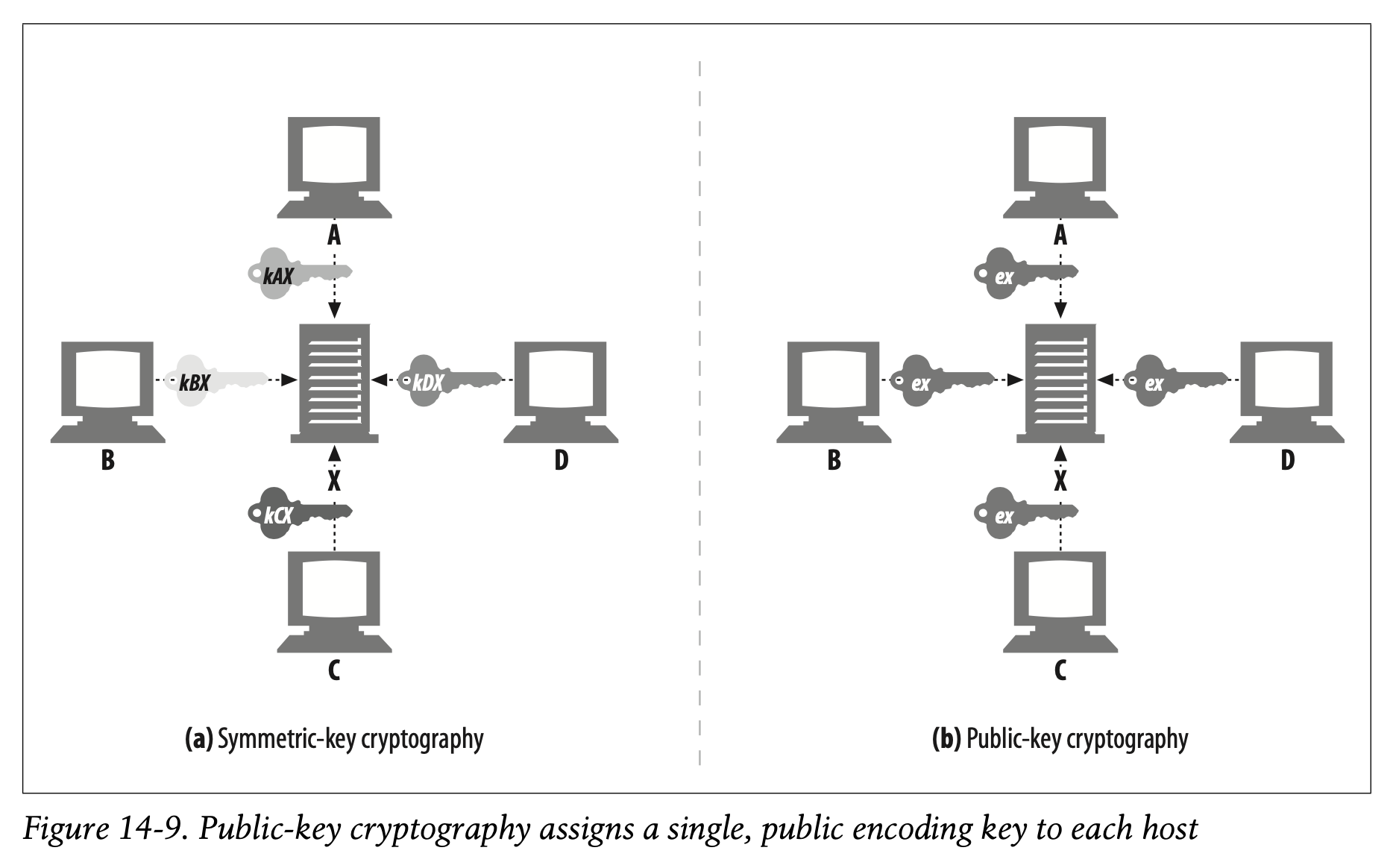
Node X can take its encoding key ex and publish it publicly.† Now anyone wanting to send a message to node X can use the same, well-known public key. Because each host is assigned an encoding key, which everyone uses, public-key cryptography avoids the N^2 explosion of pairwise symmetric keys (see Figure 14-9).

노드 X는 인코딩 키 e^x를 가져와 공개적으로 발급할 수 있습니다.
노드 X에 메시지를 전송하고자 하는 모든 사람들이 동일한 공개 키를 사용할 수 있습니다.
각각의 호스트는 모두가 공통으로 사용할 수 있는 인코딩 키를 할당 받습니다.
따라서 Public-Key Cryptography는 대칭 키를 사용할 때 N^2의 폭발적인 복잡도가 발생하는 문제를 회피할 수 있습니다.

Even though everyone can encode messages to X with the same key, no one other than X can decode the messages, because only X has the decoding private key d^x. Splitting the keys lets anyone encode a message but restricts the ability to decode messages to only the owner. This makes it easier for nodes to securely send messages to servers, because they can just look up the server’s public key.

모든 노드는 X에 대한 메시지를 동일한 키로 인코딩 하지만, X를 제외하고 이 메시지를 해독할 수 있는 노드는 없습니다.
복호화에 사용되는 비공개 키 d^x를 알고 있는 노드는 X뿐이기 때문입니다.
누구나 메시지를 인코딩 할 수 있게 키를 배포하는 것은 오직 소유자에 의해서만 메시지가 디코딩 되도록 제한합니다.
즉 서버의 Public Key를 찾기만 하면 노드가 서버에 안전하게 메시지를 전달할 수 있습니다.

Public-key encryption technology makes it possible to deploy security protocols to every computer user around the world. Because of the great importance of making a standardized public-key technology suite, a massive Public-Key Infrastructure (PKI) standards initiative has been under way for well over a decade.

Public-Key 암호화 기술은 전세계의 모든 컴퓨터 사용자에게 보안 프로토콜을 배포하는 것을 가능케 합니다.
표준화된 Public-Key 기술 제품군을 만드는 것이 중요해지면서 10년이 훨씬 넘는 기간 동안 대규모의 Public-Key Infrastructure (PKI) 표준을 구축하기 위한 노력이 이어져 와습니다.

RSA

The challenge of any public-key asymmetric cryptosystem is to make sure no bad guy can compute the secret, private key—even if he has all of the following clues:

• The public key (which anyone can get, because it’s public)

• A piece of intercepted ciphertext (obtained by snooping the network)

• A message and its associated ciphertext (obtained by running the encoder on any text)

Public-Key 비대칭 암호화의 궁극적인 과제는 공격자가 나열된 단서들을 토대로 비공개 디코딩 키를 연산할 수 없도록 보장하는 것입니다.
- 누구나 공개적으로 얻을 수 있는 Public Key
- MITM으로 가로챈 Ciphertext의 조각
- 메시지 & 메시지를 암호화한 Ciphertext(모든 텍스트를 인코딩 하여 얻은 것)

One popular public-key cryptosystem that meets all these needs is the RSA algorithm, invented at MIT and subsequently commercialized by RSA Data Security. Given a public key, an arbitrary piece of plaintext, the associated ciphertext from encoding the plaintext with the public key, the RSA algorithm itself, and even the source code of the RSA implementation, cracking the code to find the corresponding private key is believed to be as hard a problem as computing huge prime numbers—believed to be one of the hardest problems in all of computer science. So, if you can find a fast way of factoring large numbers into primes, not only can you break into Swiss bank accounts, but you can also win a Turing Award.

모든 요구사항을 만족시키는 가장 잘 알려진 Public-Key 암호화 기법은 바로 RSA 알고리즘입니다.
RSA는 MIT에서 발명하여 RSA Data Security에 의해 널리 상용화 되었습니다.
Public Key와 임의의 Plaintext, Plaintext를 Public Key로 암호화한 Ciphertext, 마지막으로 RSA 알고리즘과 이를 구현한 소스코드가 주어지더라도 일치하는 Private Key를 찾기 위해 암호를 깨뜨리는 것은 몹시 어려운 문제로 알려져 있습니다.
대규모의 소수 연산을 수행해야 하기 때문입니다.
이 문제는 컴퓨터 과학 전체를 통틀어서 가장 어려운 문제 중 하나로 손꼽힙니다.
만약 여러분이 거대한 숫자를 빠르게 소인수분해 할 수 있는 방법을 발견한다면 스위스의 은행 계좌를 해킹하는 것은 물론 Turing Award를 수상할 수도 있습니다.

The details of RSA cryptography involve some tricky mathematics, so we won’t go into them here. There are plenty of libraries available to let you perform the RSA algorithms without you needing a Ph.D. in number theory.

RSA 암호학의 세부사항은 심오한 수학적 내용을 포함하고 있으므로 여기서는 다루지 않을 것입니다.
박사 수준의 수론을 알지 못해도 RSA 알고리즘을 잘 사용할 수 있도록 이미 충분히 많은 라이브러리가 준비되어 있습니다.

Hybrid Cryptosystems and Session Keys

Asymmetric, public-key cryptography is nifty, because anyone can send secure messages to a public server, just by knowing its public key. Two nodes don’t first have to negotiate a private key in order to communicate securely.

Public Key를 알고 있다면 누구나 공개 서버에 안전하게 메시지를 전송할 수 있다는 점에서 비대칭 Public-Key Cryptography는 매우 유용합니다.
두 개의 노드가 통신을 안전하게 진행하기 위해 Private Key를 먼저 협상하는 과정이 더 이상 필요하지 않습니다.

But public-key cryptography algorithms tend to be computationally slow. In practice, mixtures of both symmetric and asymmetric schemes are used. For example, it is common to use public-key cryptography to conveniently set up secure communication between nodes but then to use that secure channel to generate and communicate a temporary, random symmetric key to encrypt the rest of the data through faster, symmetric cryptography.

하지만 Public-Key Cryptography 알고리즘은 연산 속도가 느리다는 특징이 있습니다.
때문에 실제로는 대칭, 비대칭 암호화를 혼합해서 사용합니다.
보통은 Public-Key Cryptography를 사용하여 노드간 보안 통신을 편리하게 설정하고, Symmetric Cryptography를 통해 일시적인 랜덤 대칭키를 생성하여 보안 채널로 데이터를 빠르게 전송합니다.

✏️ 요약

Public-Key Cryptography

: 모든 호스트 쌍에 대해 두 개의 비대칭 키를 활용하는 암호화 기술

Public Key : 공개적으로 알려진 키 -> 메시지 암호화에 사용
- 수신자의 Public Key로 데이터를 암호화하여 전송
Private Key : 호스트만 알고 있는 키 -> 메시지 복호화에 사용 (유출되어서는 안 됨)
- 수신자가 자신의 Private Key로 데이터를 복호화하여 해석
장점
- n^2개의 대칭 키를 관리해야 하는 문제를 회피할 수 있음
- 공개 서버의 Public Key를 알고 있으면 누구나 안전하게 메시지 전송 가능
단점
- 연산 속도가 매우 느림
RSA : 공격자가 Private Key를 유추할 수 없도록 보장하는 비대칭 암호화 알고리즘
- Public Key나 Ciphertext를 통해 Private Key를 유추할 수 없도록 설계되었음
- 대규모의 소수(Prime Number) 연산 수행
Public-Key Infrastructure(PKI) 표준을 구축하는 것이 중요

Hybrid Cryptosystems

: Symmetric Cryptography와 Public-Key Cryptography의 단점을 극복하기 위해 두 방식을 혼합하여 사용하는 기법

1. Public-Key Cryptography : 노드간 보안 통신 설정 (Symmetric 방식에 비해 키 관리가 간편하다는 점을 이용)
1. Symmetric Cryptography : 대칭키를 통해 데이터를 암호화하여 전송 (Public-Key 방식에 비해 속도가 빠르다는 점을 이용)

✏️ 감상

지나치게 위험한 도전... RSA 알고리즘을 한 번 이해해볼까?

지금껏 정규 수업과 그 밖의 다양한 자리에서 보안에 대해 논할 때, 항상 RSA에 대해서는 수도 없이 이야기해왔지만 정작 원리에 대해 논한 적은 한 번도 없었다. 그래서인지 교수님도 친구들도 알려주지 않는, ~~아니 사실 아무도 자세히 모르는 것 같은~~ 그 알고리즘의 정체가 궁금해지기 시작했다. 왠지 알고리즘에 대해 자세히 이야기하지 않는 이유가 있을 것 같아서(= 수학적인 배경지식이 많이 필요할 것 같아서) 위키피디아를 읽어볼 엄두가 잘 나지는 않지만... 일단 용기를 내서 페이지를 열었다.

RSA 알고리즘은 키를 생성하기 위해 2개의 서로 다른 소수 p와 q를 준비한다. 그리고 p와 q를 곱하여 만들어진 숫자 N과 (p-1)과 (q-1)을 곱하여 만들어진 숫자 M을 준비한다. 이때 M보다 작으면서 M과 서로소인 정수 e를 찾는다. e가 M과 서로소라는 것은 e와 M을 소인수분해 했을 때 공약수가 1밖에 없다는 뜻이다. 마지막으로 d*e를 M으로 나눴을 때 나머지가 1이 되도록 하는 d 값을 찾는다.

키값은 위의 과정을 통해 도출한 N, e, d 값을 통해 결정된다. Public Key는 <N, e>를 나타내며, Private Key는 <N, d>를 나타낸다.

암호화를 수행할 때는 Plaintext를 N보다 작은 숫자인 m으로 변환한다. 그리고 m^e를 N으로 나눈 나머지를 계산하여 Ciphertext를 생성한다. 복호화는 <N, d>를 사용하여 c^d를 N으로 나눈 나머지를 계산함으로써 이루어질 수 있다. 이게 가능하다는 것은 c^d를 N으로 나눈 나머지가 결국 m을 N으로 나눈 나머지와 동일해야 한다는 뜻인데(그래야 복호화가 가능하니까)... 도대체 어떻게 되는 걸까?

주어진 식들에 의하여 c^d는 (m^e)^d=m^{de}와 같고 de는 상수 k에 대하여 k(p-1)(q-1)+1로 표현될 수 있다. 즉 m^{k(p-1)(q-1)+1} = (m^{p-1})^{k(q-1)}*m이다.

이제 골 때리는 부분은 여기서부터다. 지금부터는 '페르마의 소정리'라는 것을 이해해야 하는데 나도 수학과가 아니라 이 정리가 왜 성립하는지 증명하는 것은 어렵고... 간단하게 예를 들어 설명해보겠다.

페르마의 소정리는 쉽게 말해 다음과 같다. p가 소수이고 a가 p로 나누어지지 않는 숫자라면, a^p를 p로 나누었을 때의 나머지와 a를 p로 나누었을 때의 나머지가 서로 같다는 것이다. p가 5고, a가 4라고 해보자. 4의 5제곱은 1024다. 1024를 5로 나누나, 4를 5로 나누나 나머지는 4로 동일하다. 해당 정리에서 a^(p-1)을 p로 나누었을 때의 나머지는 1을 p로 나누었을 때의 나머지, 즉 1이라는 점도 함께 파생된다.

다시 RSA 알고리즘으로 돌아가서 c^d=(m^{p-1})^{k(q-1)}*m라는 식을 살펴보겠다. 이 식은 m을 계속해서 제곱하고 있다. 때문에 m이 p의 배수가 아니라면 m과 p는 반드시 서로소일 수밖에 없다. p가 소수이기 때문이다.

m이 p의 배수가 아니라는 가정하에 m^{p-1}을 p로 나누었을 때의 나머지는 항상 1을 p로 나누었을 때의 나머지와 같다. 그러므로 (m^{p-1})^{k(q-1)}*m을 p로 나눈 나머지는 1^{k(q-1)}*m을 p로 나눈 나머지와 같다. 결국 1^{k(q-1)}*m = m이므로 이 값은 m을 p로 나눈 나머지와 같다. (m^{p-1})^{k(q-1)}*m를 q로 나눈 나머지가 m을 q로 나눈 나머지와 같다는 사실도 동일한 방식으로 증명할 수 있다.

m이 p의 배수라면 (m^{p-1})^{k(q-1)}*m을 p로 나눈 나머지와 m을 p로 나눈 나머지가 0으로 동일할 것이며, 이는 q로 나누었을 때도 마찬가지다. 따라서 m이 p의 배수든 아니든 위 식은 항상 성립한다.

결국 m modulo p 와 m modulo q 값이 같다는 것은 m을 p와 q의 공배수로 나누어도 동일한 나머지가 나옴을 의미한다. 그러므로 (m^{p-1})^{k(q-1)}*m를 N으로 나눈 나머지와 m을 N으로 나눈 나머지가 서로 같다. 이로써 c^d를 N으로 나눈 나머지와 m을 N으로 나눈 나머지가 동일하다는 사실을 증명할 수 있다.

역시 아무도 알고리즘에 대해 말을 꺼내지 않는 데는 이유가 있었다. 모듈로 연산은 항상 신기하고 기괴한 결론을 내놓는 것 같다. 도대체 어떤 무시무시한 사람이 RSA 알고리즘을 만든 걸까. 사고 방식이 도대체 어떻게 되어야 이 아이디어가 떠오를 수 있는 걸까...ㅋㅋㅋㅋㅋ 진짜 이해할 수가 없다.