PJT1. 서울시 평균기온 예측(with DACON)

낭만IT·2024년 1월 9일
데이터분석딥러닝머신러닝인공지능
0

데이터사이언스 프로젝트

목록 보기
3/3
post-thumbnail

나의 첫 해커톤 참가이다.
수상이 목표가 아니라 그동안 배웠던 것을 실제로 잘 쓸 수 있는지 스스로 테스트해보기 위함이고, 목표는 100등 안에 드는 것이다.

💡프로젝트 개요

- 일정: 2023. 12. 16. ~ 24. 1. 7.

- 주제: 서울시의 평균기온을 예측하는 AI 알고리즘 개발

💻 기술스택: Python, Tensorflow, Keras, matplotlib, pandas, numpy, seaborn, scikit learn, ML/DL

🗃️ 사용 알고리즘

- LSTM: 기존의 RNN에서 출력과 멀리 있는 정보를 기억할 수 없다는 단점을 보완하여 장/단기 기억을 가능하게 설계한 신경망의 구조이다. 주로 시계열 처리나, 자연어 처리에 사용

- Prophet: Meta(舊Facebook)에서 개발한 시계열 예측 모델이다. 간단하면서도 강력한 모델로, 일상적인 시계열 데이터에 대한 예측을 수행하는 데 사용된다. 이 모델은 주로 계절성, 휴일 효과, 이상치 등을 처리하는데 특화

📍프로젝트 순서

데이터수집 ▶️ 결측치 처리 및 컬럼 수정 ▶️ EDA ▶️ Feature Engineering ▶️ 모델학습 ▶️평가 ▶️예측

1. 데이터 수집

데이콘 제38회 해커톤 '서울시 평균기온 예측' 데이터 활용
https://dacon.io/competitions/official/236200/data

1.1. 데이터 소개

  • 일시, 최고기온, 최저기온, 일교차, 강수량, 평균습도, 평균풍속, 일조합, 일사합, 일조율, 평균기온(Target)
    총 10개의 컬럼이 있으며 평균기온이 Target 값이다.
  • 1960~2022년까지의 데이터가 있다.
data = pd.read_csv('/content/drive/MyDrive/data/train.csv')
data.describe()

  • raw data의 전체적인 개요이다.

1.2. 라이브러리 import

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline

import seaborn as sns
from google.colab import drive
import datetime
import sys
import matplotlib
import warnings
warnings.filterwarnings(action='ignore')

import tensorflow as tf


# 한글 폰트
if 'google.colab' in sys.modules:
    !sudo apt-get -qq -y install fonts-nanum
    import matplotlib.font_manager as fm
    font_files = fm.findSystemFonts(fontpaths=['/usr/share/fonts/truetype/nanum'])
    for fpath in font_files:
        fm.fontManager.addfont(fpath)

matplotlib.rc('font', family='NanumBarunGothic')
matplotlib.rcParams['axes.unicode_minus'] = False

from statsmodels.datasets.longley import load_pandas
import statsmodels.api as sm
from statsmodels.stats.outliers_influence import variance_inflation_factor
plt.rc('font', family='NanumBarunGothic') ## 한글 폰트

1.3. '일시'컬럼을 index로 변환

# 날짜 데이터 변환
data['일시'] = pd.to_datetime(data['일시'])
data = data.set_index('일시')

# 데이터의 시간 간격 지정
data.index.freq = 'D'

# 일시 컬럼이 인덱스로 할당
data.info()
  • '일시' 컬럼을 to_datetime을 활용하여 날짜형식으로 변경해준다.
  • 데이터의 시간 간격을 'D'로하여 기준을 일로 설정해준다.

2. 결측치 처리 및 컬럼 수정

# 컬럼별 결측치 확인
data.columns
for i in data.columns:
    print(data[i].isnull().value_counts())
    print()
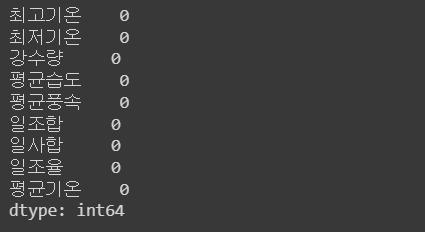
    print(data[data[i].isna()])
  • 결측치를 확인해보면 모든 컬럼에서 결측치가 발견이 된다. EDA 및 모델학습을 위해 결측치 처리 진행하겠다.

2.1. '최고기온/최저기온' 컬럼 결측치 처리

# 결측치 처리
# 최고기온 : 2월, 10월이 결측치가 있으니 각 년도 2월, 10월 각 평균으로 입력
data.loc['1967-02-19', '최고기온'] = data.loc['1967-02-01':'1967-02-28', '최고기온'].mean()
data.loc['1973-10-16', '최고기온'] = data.loc['1973-10-01':'1973-10-31', '최고기온'].mean()
data.loc['2017-10-12', '최고기온'] = data.loc['2017-10-01':'2017-10-31', '최고기온'].mean()

# 최저기온 : 각 년도 2, 8, 10월 평균으로 결측치 처리
data.loc['1967-02-19', '최저기온'] = data.loc['1967-02-01':'1967-02-28', '최저기온'].mean()
data.loc['1973-10-16', '최저기온'] = data.loc['1973-10-01':'1973-10-31', '최저기온'].mean()
data.loc['2022-08-08', '최저기온'] = data.loc['2022-08-01':'2022-08-31', '최저기온'].mean()
data['최저기온'].isnull().sum()

data.drop('일교차', axis = 1, inplace = True)
data.isnull().sum()
  • 결측치가 발생한 컬럼의 년/월 평균으로 결측치를 처리했다.
  • '일교차' 컬럼은 최고기온과 최저기온의 차이이기에 다중공선성을 고려하여 drop했다.
    즉, 일교차는 최고/최저기온의 종속변수이다.
    * 다중공선성 : 하나의 독립변수가 다른 여러 개의 독립변수들로 잘 예측되는 경우

2.2. '강수량' 컬럼 결측치 처리

# 강수량 : 결측치 : 13861개
data[data['강수량'].isna()].index

data['강수량'].fillna(0.0, inplace = True)
data['강수량'].isnull().sum()
  • 강수량이 NaN값인 이유는 측정할 수 없을 만큼 비가 왔다는 것으로 판단 -> 0.0으로 결측치 처리

2.3. '평균풍속' 컬럼 결측치 처리

data.loc['1983-07-16', '평균풍속'] = data.loc['1983-07-01':'1983-07-30', '평균풍속'].mean()
data.loc['2017-10-14', '평균풍속'] = data.loc['2017-10-01':'2017-10-31', '평균풍속'].mean()
data.loc['2017-12-05':'2017-12-07', '평균풍속'] = data.loc['2017-12-01':'2017-12-31', '평균풍속'].mean()
data['평균풍속'].isnull().sum()
  • 각 년도의 결측치가 있는 월 평균으로 결측치를 처리했다.

2.4. 일조합/일사합/일조율 결측치 처리

# 일조합 결측 : 118개, 일사합 결측 : 4862개

 # 선형보간 사용(interpolate) -> method = 'linear'
cols = ['일조합', '일사합', '일조율']
for col in cols:
    data[col].interpolate(method = 'linear', inplace = True)

# 일사합 및 일조율이 1972년까지 결측치 처리가 안 됨 -> 1972년까지의 행을 drop
data = data.loc['1973-01-01':,:]
  • 선형보간법을 사용하여 결측치를 처리했다.
  • 한 가지 이슈가 발생했는데, 일사합과 일조율이 1972년까지의 데이터에 대해 결측치 처리가 되지 않았다. 그래서 해당 행들을 drop을 시키고 진행했다.

2.5. '계절' 컬럼 생성

for i in data.index:
    if i.month in [3, 4, 5]:
        data.loc[i, '계절'] = "봄"
    elif i.month in [6, 7, 8]:
        data.loc[i, '계절'] = '여름'
    elif i.month in [9, 10, 11]:
        data.loc[i, '계절'] = '가을'
    else:
        data.loc[i, '계절'] = '겨울'
  • 각 월에 맞게 사계절을 설정하여 '계절' 컬럼을 생성

3. EDA

3.1. 최고/최저기온, 강수량, 평균기온 추이

plt.figure(figsize = (1,1))
plot_cols = ['최고기온', '최저기온', '강수량', '평균기온']
plot_features = data[plot_cols]
plot_features.index = data.index
_ = plot_features.plot(subplots = True)

# 2000년 월별 추이(1972~2022년 중 중간 년도 선택)
plot_features = data[plot_cols][9861:10227]
plot_features.index = data.index[9861:10227]
_ = plot_features.plot(subplots=True)

[최고/최저기온, 강수량, 평균기온 추이]

[2000년 월별 추이(1972~2022년 중 중간 년도 선택)]

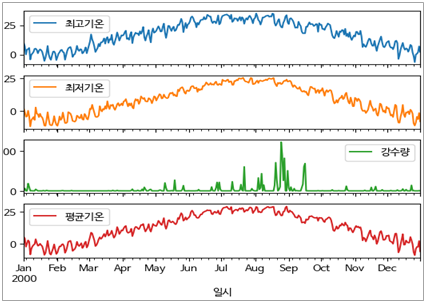
  • 12월 ~ 2월 중순까지 영하의 온도
  • 8월 중순 ~ 9월초까지 강수량이 비약적으로 많다.

3.2. 평균기온별 컬럼 분석

3.2.1. 평균기온별 강수량

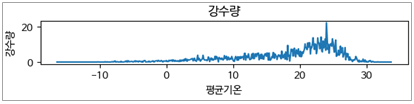
  • 평균기온과 강수량이 비례하나, 20~30도 사이에 강수량이 비약적으로 상승
  • 20~30도 사이에 강수량이 비약적으로 상승하는 구간은 장마기간으로 예상
  • 기온이 20도 후반으로 갈수록 강수량이 하락하는 것으로 보아 장마가 끝난 뒤 무더위가 시작되는 것으로 보임

3.2.2. 평균기온별 평균습도

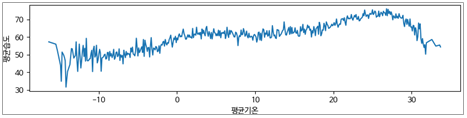
  • 강수량과 비슷한 추이를 보임
  • 단, -10도 미만에서 평균습도의 편차가 큰 것으로 보아 겨울철의 폭설 및 건조기후를 예상(습도는 강수량을 제외한 다양한 기후영향을 받음)

3.2.3. 평균기온별 평균풍속

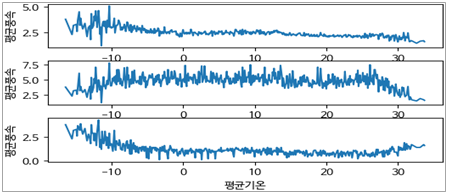
  • 첫 번째 그래프부터 평균풍속의 평균, 최대 평균풍속, 최소 평균풍속 순이다.
  • 기온이 낮을수록 평균풍속이 높은 경향이지만, -10도 미만일 때 편차가 심하다
  • 최대, 최소 평균풍속을 보아 겨울철이 대체로 평균풍속이 높고, 타 계절은 고르게 분포되어 있다.
  • 하지만 최대/최소 평균풍속은 특수상황(강풍, 태풍 등)일 가능성에 따라 분석에는 참고만 하는 것이 좋을 것 같다.

3.2.4. 평균기온에 따른 일조합, 일사합, 일조율의 평균

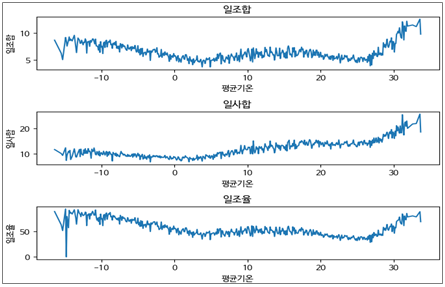
  • 20도 후반 ~ 30도 중반까지 일조합이 최대로 증가하는 것으로 보아 여름임을 예측
  • 평균기온이 최저에서 4~5도로 갈수록 일조합 감소
  • 평균기온과 일사합은 비례
  • -10도 이하에서 최저의 일조율을 보임
  • 평균기온이 증가 할수록 일조율이 감소 및 유지하는 것으로 보이나, 20도 후반~부터는 급상승 경향

3.2.5. 평균기온에 따른 최고/최저기온의 평균

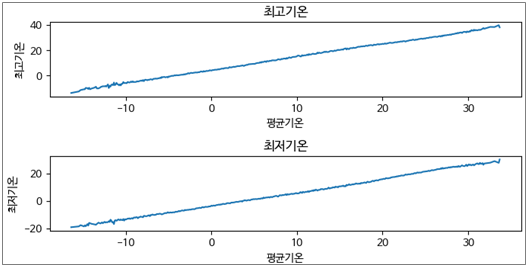
  • 평균기온과 최고/최저기온은 비례한다.

3.2.6. 평균기온에 따른 일교차 추이

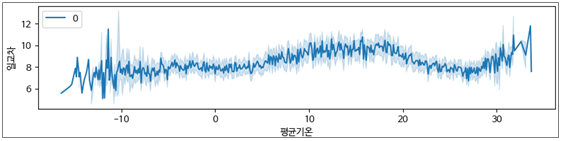
  • -10도 미만에서 일교차의 편차가 크다
  • 10~20도에서 일교차가 높은 경향을 보임

    ☞ 평균기온별 각 컬럼을 분석 결과

    → 평균기온 -10도에서 모든 컬럼들의 편차가 크게 나타났다. 이상치처럼 보일 수 있으나, 실제 기후데이터의 경향이며 삭제하거나 fitting을 하면 추후 모델 성능이 떨어지거나 overfitting 가능성이 있으므로 그대로 유지하기로 판단

3.3. 계절별 컬럼 분석

3.3.1. 계절에 따른 최고/최저/평균기온의 평균

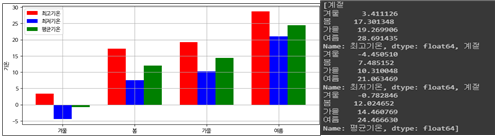
  • 계절별 평균기온 - 봄: 약 12도 / 여름: 약24도 / 가을: 약 14도 / 겨울: 약 -1도
  • 봄이 가장 일교차가 크다
  • 최고/최저기온의 평균은 겨울 → 봄 → 가을 → 여름 순이다.
  • 봄이 가을보다 평균적으로 기온이 낮은 경향

3.3.2. 계절에 따른 강수량 및 평균습도의 평균

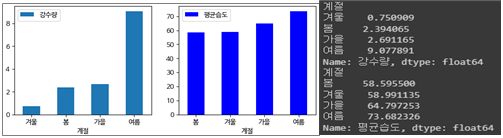
  • 강수량 및 평균습도는 여름이 가장 높다.
  • 강수량은 겨울이 가장 낮으나, 평균습도는 미세하지만 봄이 가장 낮다(겨울과 거의 동일)
    • 봄이 타계절에 비해 건조하다는 것을 도출 할 수 있다.
    • 겨울은 강수량이 적으니 평균습도도 낮은 편이다.
  • 사계절 모두 평균습도는 60~75이다.
  • 강수량과 평균습도가 비례한 경향은 아닌 것으로 보임. 평균습도는 강수량을 제외한 다른 요소들의 영향도 있는 것으로 분석

3.3.3. 계절에 따른 평균풍속 및 평균습도

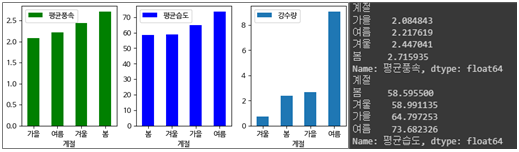
  • 평균풍속 : 봄 > 겨울 > 여름 > 가을 순
  • 평균습도 : 여름 > 가을 > 겨울 > 봄 순
  • 강 수 량 : 여름 > 가을 > 봄 > 겨울 순
  • 풍속이 높은 편인 겨울 및 봄은 습도가 하위에 속함
  • 풍속이 평균습도에 어느정도 영향을 미치는 것으로 분석

3.3.4. 계절에 따른 일조합, 일사합, 일조율

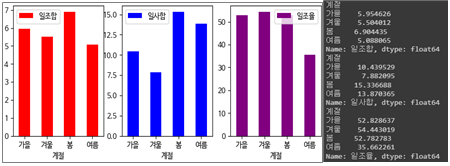
  • 봄의 일사합 및 일조합이 가장 높으나, 일조율은 겨울이 가장 높다.
  • 여름의 일사합이 높은 경향이나, 일조합이 낮은 경향인 이유는 강수가 많아 흐린날씨가 원인인 것으로 분석
  • 가을 및 겨울의 일사합이 봄처럼 비례하지 못한 이유는 가을 및 겨울의 가조시간이 짧기 때문인 것으로 분석(가조시간 : 해가 떠있는 시간)
  • 여름의 일조율이 현저히 작은 이유는 일조시간이 가장 적고 가조시간은 가장 길기 때문인 것으로 분석
  • 일사합은 계절의 영향을 많이 받고, 일조합은 강수량의 영향을 많이 받으며, 일조율은 일조합의 영향을 많이 받는 것으로 파악

3.4. 상관관계 확인

mask = np.triu(np.ones_like(data.corr(), dtype=np.bool))
sns.heatmap(data.corr(method = 'pearson', min_periods =1), annot = True, mask = mask)
plt.xticks(rotation = 45)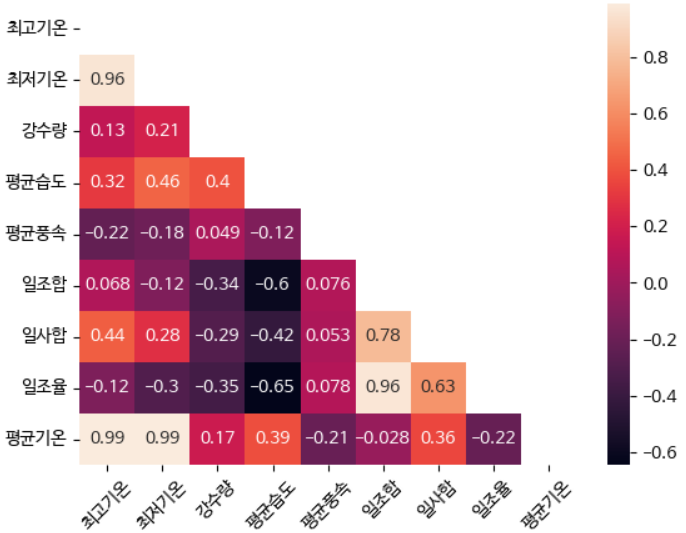

  • 피어슨 상관계수 확인
    • 1, -1과 가까울수록 상관관계가 높다
    • 0에 가까울수록 상관관계가 낮다
    • 평균기온, 최저기온, 최고기온은 서로 상관관계가 매우 높다.
    • 평균풍속은 일조율, 일사합, 일조합과 상관관계가 매우 낮다
    • 일조합, 일사합, 일조율은 서로 상관관계가 높다. 특히, 일조율과 일사합은 상관관계가 매우 높다

4. Feature Engineering

4.1. 이상치 제거

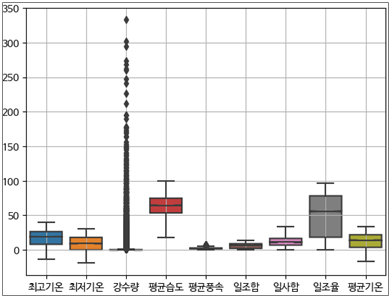
  • Boxplot을 활용하여 이상치 확인
  • 강수량 및 평균풍속 에서 큰 이상치 발견
  • Overfitting을 방지하기 위해 평균 분포보다 지나치게 큰 값 제거

4.1.1. 강수량 이상치 확인

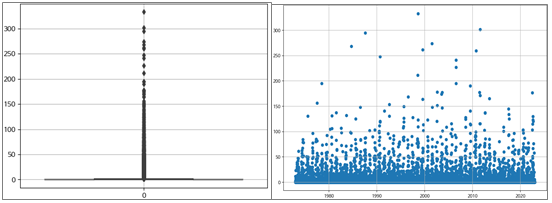
  • Boxplot, scatter 활용
  • 기후데이터이기에 이상치도 의미있는 데이터일 가능성이 있으나, 태풍 혹은 폭우 등의 특이 케이스 가능성이 있으니 280이상은 제거
  • 강수량 및 평균풍속은 모델검증하면서 이상치 처리를 통한 연구 필요

4.1.2. 평균풍속 이상치 확인

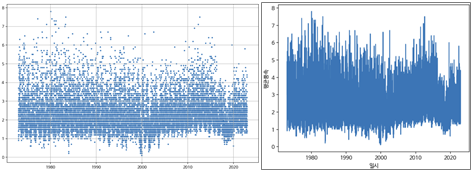
  • scatter, lineplot 활용
  • 기후데이터이기에 이상치도 의미있는 데이터일 가능성이 있으나, 태풍 혹은 강풍일 가능성이 있으니 7이상은 제거

4.1.3. 나머지 컬럼 이상치 확인 및 처리

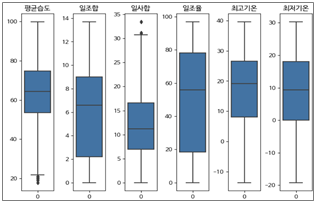
[ IQR 기반 이상치 제거]

Q1 = data[['평균습도','일사합', '일조율','최고기온', '최저기온']].quantile(q=0.25)
Q3 = data[['평균습도', '일사합', '일조율', '최고기온', '최저기온']].quantile(q=0.75)

print(Q1, Q3)
IQR = Q3 - Q1

IQR_df = data[(data['평균습도'] <= Q3['평균습도'] + 1.5 * IQR['평균습도']) & (data['평균습도'] >= Q1['평균습도'] - 1.5 * IQR['평균습도'])]
IQR_df = IQR_df[(IQR_df['일사합'] <= Q3['일사합'] + 1.5 * IQR['일사합']) & (IQR_df['일사합'] >= Q1['일사합'] - 1.5 * IQR['일사합'])]
IQR_df = IQR_df[(IQR_df['일조율'] <= Q3['일조율'] + 1.5 * IQR['일조율']) & (IQR_df['일조율'] >= Q1['일조율'] - 1.5 * IQR['일조율'])]
IQR_df = IQR_df[(IQR_df['최고기온'] <= Q3['최고기온'] + 1.5 * IQR['최고기온']) & (IQR_df['최고기온'] >= Q1['최고기온'] - 1.5 * IQR['최고기온'])]
IQR_df = IQR_df[(IQR_df['최저기온'] <= Q3['최저기온'] + 1.5 * IQR['최저기온']) & (IQR_df['최저기온'] >= Q1['최저기온'] - 1.5 * IQR['최저기온'])]

💡 IQR 개념

- 제1사분위수 = Q1(25%)
- 제3사분위수 = Q3(75%)
- IQR = Q3 - Q1
 * IQR 범위 값 구하기
 	Q1 - 1.5 * IQR <= values <= Q3 + 1.5 * IQR
    ☞ 해당 범위 안에 있는 값만 보존

4.2. Encoding

  • '계절' 컬럼의 type은 str이므로 Label encoding 필요
    • 1 : 겨울 / 2 : 봄 / 3 : 여름 / 4 : 가을
from sklearn.preprocessing import LabelEncoder
encoder = LabelEncoder()
IQR_df['계절'] = encoder.fit_transform(IQR_df['계절'])

5. 모델학습(Prophet)

5.1. 라이브러리 import

import prophet
from prophet import Prophet
from sklearn.metrics import mean_absolute_error
  • Prophet 모델을 사용하기 위해 import
  • 성능평가 지표는 MAE(평균절대오차)

5.2. 학습을 위한 데이터 튜닝

df = df.reset_index()
df = df.rename(columns={'일시': 'ds', '평균기온': 'y'})
  • Prophet 모델은 데이터를 인식할 수 있도록 일시는 'ds'로 target값인 '평균기온'은 'y'로 지정 필요
  • 또한, index로 지정했던 '일시'는 다시 컬럼으로 reset

5.3. 데이터셋 분리

train_size = int(0.8 * len(df))
val_size = int(0.1 * len(df))
test_size = len(df) - train_size - val_size

train_df = df[:train_size]
val_df = df[train_size:train_size+val_size]
test_df = df[train_size+val_size:]
  • Train, Validation, Test셋으로 8:1:1로 분리

5.4. 모델학습

prophet = Prophet(changepoint_prior_scale=0.5,
                  daily_seasonality=True,
                  seasonality_mode = 'additive',
                  seasonality_prior_scale = 10)
prophet.fit(train_df)

- 파라미터 설명

  • changepoint_prior_scale=0.5 : 추세에 따라 데이터를 유연하게 반영할 건지 추세에 유연하지 않게 반영할 건지 결정하는 parameter(default = 0.05)
    ☞ 데이터 추세가 일정하지만 약간의 변수가 있어 유연성 반영률을 높임
  • daily_seasonality=True : 데이터와 일간 계절성 연관성 여부 설정
    ☞ 데이터가 일자별 데이터에 따라 True로 설정
  • seasonality_mode = 'additive' : ‘additive’와 ‘multiflicative’ 옵션
    •'additive' : 시계열 데이터가 진폭이 일정할 때 사용
    •'multiflicative' : 시계열 데이터의 진폭이 점점 증가하거나 감소할 때 사용
    ☞ 데이터 진폭이 일정함으로 ‘additive’로 설정
  • seasonality_prior_scale = 10 : 계절의 유연성을 제어하는 parameter 값이 크면 계절성의 영향이 커지고 값이 작아지면 계절성의 영향이 줄어듦
    ☞ 0.01 ~ 10 사이의 범위가 가장 적절하며 해당 데이터는 계절성의 영향이 큼으로 10로 설정

5.6. 검증 및 평가

plt.figure(figsize = (8, 3))

# validation 데이터를 사용하여 모델 예측(optional)
future_val = prophet.make_future_dataframe(periods = val_size)
forecast_val = prophet.predict(future_val)

# 검증 데이터와 예측값 비교
fig = prophet.plot(forecast_val)
plt.title('validaition')

# 검증 데이터에 대한 평가 지표 계산 (예: 평균제곱오차)
mae = mean_absolute_error(val_df['y'], forecast_val['yhat'][:val_size])
print(f'Mean Squared Error on Validation Data: {mae}')

# test 데이터를 사용하여 최종 예측 수행
future_test = prophet.make_future_dataframe(periods=test_size)
forecast_test = prophet.predict(future_test)

# test 데이터와 예측값 비교
fig = prophet.plot(forecast_test)
plt.title('test')

# test 데이터에 대한 평가 지표 계산D
mae_test = mean_absolute_error(test_df['y'], forecast_test['yhat'][-test_size:])
print(f'Mean Squared Error on Test Data: {mae_test}')

검증결과 : 2.8194 / 평가결과 : 2.8751

* Blue Line = 예측값 / Black dot = 실제값
[Validation 데이터 성능 시각화]

[Test 데이터 성능 시각화]

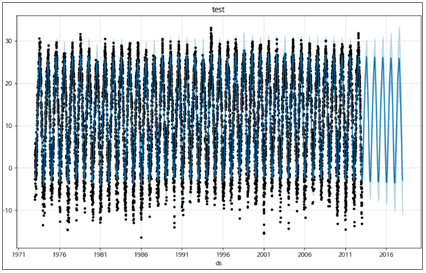
  • 실제값과 예측값의 차이가 각 년도 최고/최저 평균기온에서 차이가 나지만 대체로 동일한 경향을 띈다.
  • 예측값은 진폭이 일정한 경향이지만, 실제값은 진폭이 비교적 크며 이상치들이 종종 발견된다.

5.7 예측

future_data = prophet.make_future_dataframe(periods = 358, freq = 'd') #periods는 예측할 기간
forecast_data = prophet.predict(future_data)
forecast_data[['ds','yhat']].tail()
  • Prophet 모델 안에는 ‘make_future_dataframe’이라는 메서드가 있으며, 미래에 대한 예측값은 DataFrame 형식으로 생성해주는 기능이 있다.
    • periods : 예측할 데이터의 index 개수를 지정(예측할 기간)
    • freq : 예측 기준(d : day / m : month / y : year)
  • 검증 및 하이퍼파라미터 튜닝 후, 위의 방법으로 예측 기간과 기준을 설정한 뒤 예측을 시행한다.
submission_df = pd.read_csv('/content/drive/MyDrive/data/sample_submission.csv')

submission_df['평균기온'] = forecast_data.yhat[-358:].values
submission_df.tail()

#결과 저장
submission_df.to_csv("submission_prophet_final2.csv", index=False)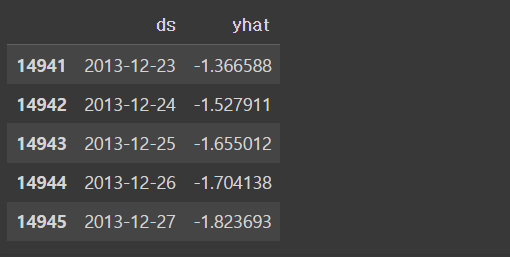


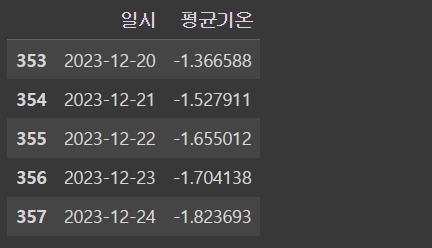
  • 앞에서 예측한 값을 실제 23년용 평균기온 csv파일에 일시 순으로 저장

6. 모델학습(LSTM)

6.1. 데이터셋 분리

column_indices = {name: i for i, name in enumerate(df.columns)}

n = len(df)

train_df = df[0:int(n*0.7)]
val_df = df[int(n*0.7):int(n*0.9)]
test_df = df[int(n*0.9):]

num_features = df.shape
print(num_features)
  • 현재 ‘일자’가 index로 지정되어 있음에 따라 ‘enumerate’ 함수를 통해 새로운 인덱스 생성
  • Train, Validation, Test셋으로 7:2:1로 분리

6.2. 정규화(Normalization)

  • 모델의 성능을 향상시키기 위해 데이터 정규화를 시행
  • 평균 및 표준편차 기반의 정규화 진행
  • 단, 모델 성능평가 결과, Prophet은 정규화 진행시 예측값과 평기지표가 낮게 나와서 정규화 미시행
train_mean = train_df.mean()
train_std = train_df.std()

train_df = (train_df - train_mean) / train_std
val_df = (val_df - train_mean) / train_std
test_df = (test_df - train_mean) / train_std

6.3. WindowGenerator 생성(tensorflow 홈페이지 참고)

  • Window 개념: 시계열 데이터나 시퀀스 데이터를 처리할 때 사용되는 개념이며, 데이터를 일정한 크기의 창 또는 기간으로 나누어서 처리하는 방법. Window 기법은 데이터를 일정한 크기의 부분 집합으로 분할하여 모델에 입력하는 방식으로 사용.
  • LSTM은 입력으로 고정된 크기의 시퀀스를 요구됨. window를 사용하면 가변 길이의 시퀀스를 고정된 크기로 자를 수 있어 LSTM에 입력으로 사용하기 편리
  • LSTM 모델을 처음 사용해보는데, 데이터의 input_size가 맞지 않다는 오류가 계속 발생했다.
  • 여러 문서들을 찾아본 결과 Window 기법을 활용해야한다는 것을 알게되었다.
  • 하지만, 아직 Window에 대한 정확한 이해가 없어서 Tensorflow 홈페이지의 코드를 참고했다.

[Window 생성 class 정의]

class WindowGenerator():
  def __init__(self, input_width, label_width, shift,
               train_df=train_df, val_df=val_df, label_columns=None):
    # Store the raw data.
    self.train_df = train_df
    self.val_df = val_df

    # Work out the label column indices.
    self.label_columns = label_columns
    if label_columns is not None:
      self.label_columns_indices = {name: i for i, name in
                                    enumerate(label_columns)}
    self.column_indices = {name: i for i, name in
                           enumerate(train_df.columns)}

    # Work out the window parameters.
    self.input_width = input_width
    self.label_width = label_width
    self.shift = shift

    self.total_window_size = input_width + shift

    self.input_slice = slice(0, input_width)
    self.input_indices = np.arange(self.total_window_size)[self.input_slice]

    self.label_start = self.total_window_size - self.label_width
    self.labels_slice = slice(self.label_start, None)
    self.label_indices = np.arange(self.total_window_size)[self.labels_slice]

  def __repr__(self):
    return '\n'.join([
        f'Total window size: {self.total_window_size}',
        f'Input indices: {self.input_indices}',
        f'Label indices: {self.label_indices}',
        f'Label column name(s): {self.label_columns}'])

[분할함수 정의]

  • 연속적인 입력값이 주어지면 split_window 메서드는 이 값을 입력 창과 레이블 창으로 변환
def split_window(self, features):
  inputs = features[:, self.input_slice, :]
  labels = features[:, self.labels_slice, :]
  if self.label_columns is not None:
    labels = tf.stack(
        [labels[:, :, self.column_indices[name]] for name in self.label_columns],
        axis=-1)

  # Slicing doesn't preserve static shape information, so set the shapes
  # manually. This way the `tf.data.Datasets` are easier to inspect.
  inputs.set_shape([None, self.input_width, None])
  labels.set_shape([None, self.label_width, None])

  return inputs, labels

WindowGenerator.split_window = split_window

[tf.data.Dataset 만들기]

  • 해당 메서드는 시계열 DataFrame을 가져와 tf.keras.utils.timeseries_dataset_from_array 함수를 이용해 (input_window, label_window)쌍의 tf.data.Dataset로 변환
def make_dataset(self, data):
  data = np.array(data, dtype=np.float32)
  ds = tf.keras.utils.timeseries_dataset_from_array(
      data=data,
      targets=None,
      sequence_length=self.total_window_size,
      sequence_stride=1,
      shuffle=True,
      batch_size=32,)

  ds = ds.map(self.split_window)

  return ds

WindowGenerator.make_dataset = make_dataset

[@property를 통한 메서드 엑세스 간편화]

@property
def train(self):
  return self.make_dataset(self.train_df)

@property
def val(self):
  return self.make_dataset(self.val_df)

@property
def example(self):
  """Get and cache an example batch of `inputs, labels` for plotting."""
  result = getattr(self, '_example', None)
  if result is None:
    # No example batch was found, so get one from the `.train` dataset
    result = next(iter(self.train))
    # And cache it for next time
    self._example = result
  return result

WindowGenerator.train = train
WindowGenerator.val = val
WindowGenerator.example = example
  • ‘@property’ 기능은 클래스의 속성을 정의하고, 사용할 수 있게 하는 데코레이터
  • ‘@property’를 사용하면 해당 속성에 접근할 때 일잔적인 속성처럼 보이지만, 실제로는 메서드를 호출하는 것과 같이 특별한 동작을 수행할 수 있음
  • 기본적으로 클래스 속성은 해당 속성에 직접 접근할 때만 값을 가져오거나 설정할 수 있으나, ‘@propert’를 사용하면 이러한 속성을 메서드로 대체하여 속성에 접근하거나 값은 설정할 때 추가적인 동작 수행할 수 있음.

6.4. 모델 컴파일

MAX_EPOCHS = 110

def compile_and_fit(model, window, patience=5):
  early_stopping = tf.keras.callbacks.EarlyStopping(monitor='val_loss',
                                                    patience=patience,
                                                    mode='min',
                                                    restore_best_weights=True)

  model.compile(loss=tf.keras.losses.MeanSquaredError(),
                optimizer=tf.keras.optimizers.SGD(),
                metrics=[tf.keras.metrics.MeanAbsoluteError()])

  history = model.fit(window.train, epochs=MAX_EPOCHS,
                      validation_data=window.val,
                      callbacks=[early_stopping])
  return history
  • ‘EarlyStopping’ 함수를 이용하여 최대 성능평가값이 나오면 학습을 중단할 수 있도록 설정
  • loss 함수 : MSE(Mean Squared Error)
  • optimizer : SGD
    ※ Adam과 비교했을 때 SGD가 성능이 더 높게 평가됨
  • metrics(성능지표) : MAE(Mean Absolute Error)
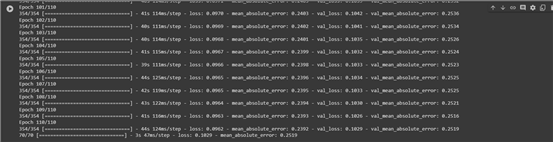
  • 모델학습시, epochs = 90~110(110이 가장 성능이 좋음) 설정

6.5. Window를 활용한 데이터 형태 변환

OUT_STEPS = 358
INPUT_WIDTH = OUT_STEPS * 3
multi_window = WindowGenerator(input_width=INPUT_WIDTH,
                               label_width=OUT_STEPS,
                               shift=OUT_STEPS,
                               label_columns=['평균기온'])

multi_window.train.element_spec
  • LSTM은 입력으로 고정된 크기의 시퀀스를 요구됨에 따라 Window를 사용하면 가변 길이의 시퀀스를 고정된 크기로 자를 수 있어 LSTM에 입력으로 사용하기 편리

6.6. 모델 학습

multi_val_performance = {}
multi_performance = {}

multi_lstm_model = tf.keras.Sequential([
    # Shape [batch, time, features] => [batch, lstm_units].
    tf.keras.layers.LSTM(128, return_sequences=True),
    tf.keras.layers.LSTM(128, return_sequences=True),
    tf.keras.layers.LSTM(128, return_sequences=False),
    # Shape => [batch, out_steps*features].
    tf.keras.layers.Dense(OUT_STEPS,
                          kernel_initializer=tf.initializers.zeros()),
    # Shape => [batch, out_steps, features].
    tf.keras.layers.Reshape([OUT_STEPS, 1])
])

history = compile_and_fit(multi_lstm_model, multi_window)

# IPython.display.clear_output()

multi_val_performance['LSTM'] = multi_lstm_model.evaluate(multi_window.val)
multi_performance['LSTM'] = multi_lstm_model.evaluate(multi_window.val, verbose=0)
  • LSTM 신경망 모델 생성 후, 훈련+검증+테스트 진행
  • 신경망 내 데이터의 input_shape과 output_shape을 변환하는 매개변수 설정

6.7. 모델 평가 및 예측

- 모델평가 결과: loss율 : 0.1029 / MAE : 0.2519

  • 학습이 완료된 모델을 활용하여 ’23년 평균기온 예측
input_submit = test_df[-INPUT_WIDTH:].values.reshape(1, INPUT_WIDTH, 9)
pred = multi_lstm_model.predict(input_submit)
plt.plot(pred)
prediction = pred[-1].reshape(-1,) * train_std['평균기온'] + train_mean['평균기온']

⭐ 결론

  • Prophet은 회귀분석을 기반으로 한 시계열 예측모델이며 머신러닝에 속함. Prophet은 복잡한 튜닝 없이도 간편하게 모델을 설정하고 예측 가능
  • LSTM은 순환 신경망(RNN)의 한 종류로, 시계열 데이터 및 순차적인 데이터를 모델링하는데 효과적인 모델이며 장기 기억과 단기 기억을 관리하여 시퀀스 데이터의 장기 의존성을 감지하고 유지할 수 있음
  • Prophet에 비해 LSTM이 모델링 하는데에 있어, 더욱 정교하며 파라미터의 종류도 다양함
  • 기후데이터를 여러방법으로 전처리를 수행하고 모델을 학습시켰지만 성능에 있어서 큰 차이는 보이지 않음
  • 프로젝트 진행시, Prophet 모델의 성능이 더 잘 나왔으며, LSTM의 성능을 높이기 위해서는 정교한 하이퍼파라미터 튜닝이 필요
  • 데이터 전처리에 있어서, 평균풍속 및 강수량의 이상치 처리가 keypoint이며 각 컬럼의 결측치 처리의 방식도 중요하다고 분석

🏆DACON 해커톤 결과

- Public : 90/638등

- Private : 44/624등

🤔 첫 대회치고는 꽤 괜찮은 성적인것 같다. 다만 아쉬웠던 점은 모델들을 완벽히 이해하고 사용한 것이 아니라 예제 코드들을 보면서 사용했던 것이 조금 아쉽다. 다음 대회나 프로젝트에서는 모델에 대한 연구를 깊게 하고, 전처리 방식도 고민을 해서 진행을 해야겠다.

📑참고문헌

profile
낭만IT
이전 포스트

Mini PJT(2). 캘리포니아 집값 예측(선형회귀)

0개의 댓글