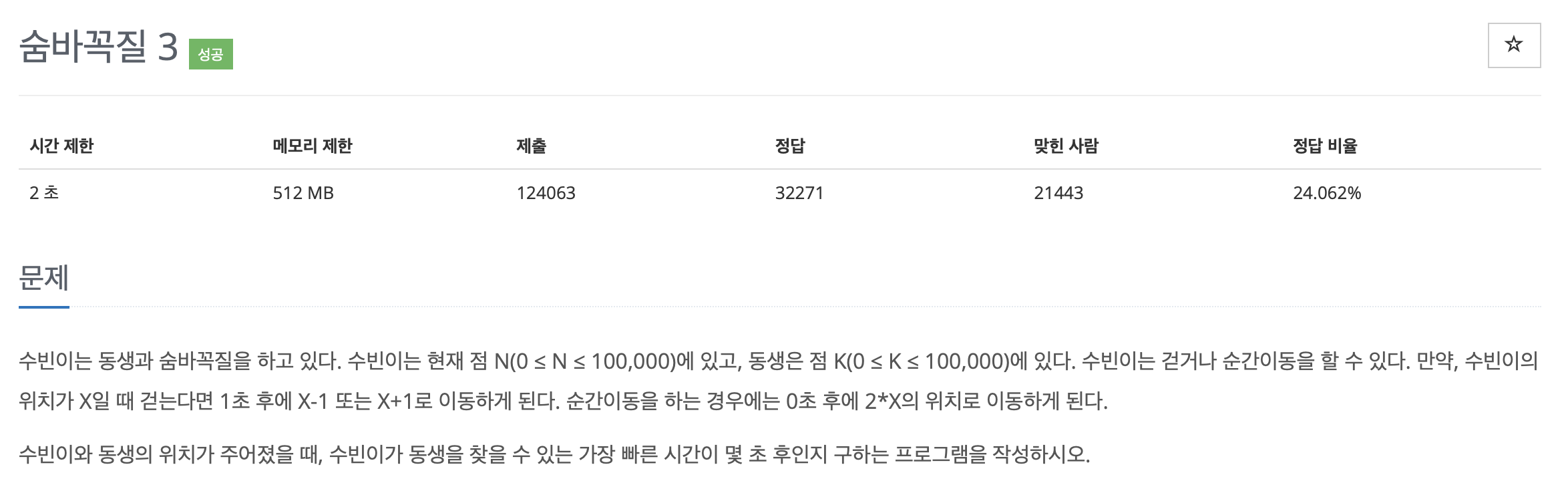
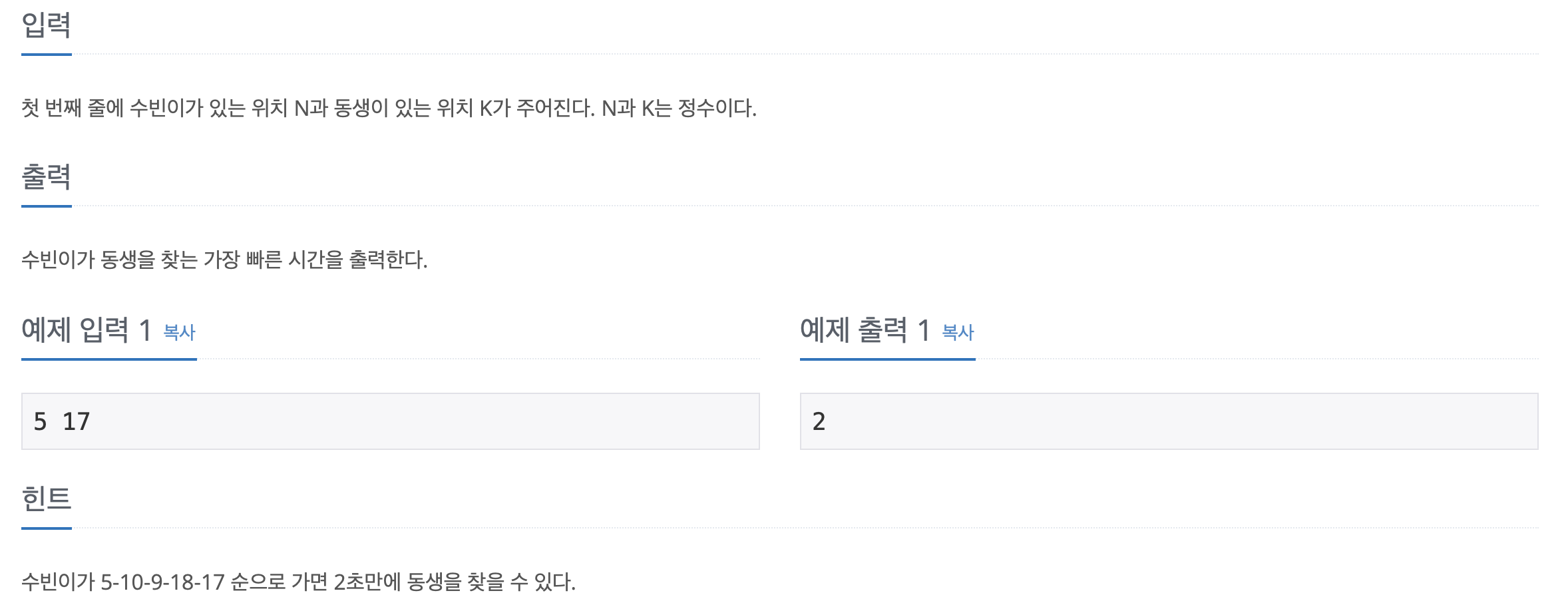
문제 및 입출력
풀이
위치를 이동할 때 시간이 0초 지날수도 1초가 지날수도 있다
이런 상황은 간선의 가중치가 0 또는 1인 그래프와 매우 유사한 상황이다
예전에 풀어봤던 숨바꼭질 1 문제에서 방향벡터를 익히게 되었는데, 이번 그래프 문제에 접목시켜서 풀면 될 것 같다는 생각이 들었다
더불어, 가중치가 동일한 경우에는 노드에 방문체크가 되어있으면 방문하지 않았는데 (최적의 거리이므로), 이 문제는 가중치가 다르므로 최단거리라 확신할 수 없으므로 노드의 방문여부를 체크할 필요가 없다고 생각했다.
static int[] dx = {-1, 1, 2};
static int[] d;
static int N, K;변수 설명
- dx: 방향벡터를 담고있는 1차원 배열
- d: 다익스트라를 사용하기 위해 최단거리를 담고있는 배열
- N,K: 입력받을 수빈이와 동생의 위치
PriorityQueue<Node> queue = new PriorityQueue<>();
Arrays.fill(d, Integer.MAX_VALUE);
d[start] = 0;다익스트라 알고리즘을 사용하기 위해 우선순위 큐를 선언한다
초기 최단거리 배열을 MAX 값으로 채우고, start 만 0으로 초기화한다
(두 코드 순서에 주의하자)
for (int i = 0; i < 3; i++) {
if ((i == 2) && (cur.node * dx[i] <= 100_000)) {
int nextNode = cur.node * dx[i];
if (d[nextNode] > d[cur.node] + 0) {
d[nextNode] = d[cur.node] + 0;
queue.add(new Node(cur.node * dx[i], d[cur.node] + 0));
}
} else if ((i == 0 || i == 1) && (0 <= cur.node + dx[i] && cur.node + dx[i] <= 100_000)) {
int nextNode = cur.node + dx[i];
if (d[nextNode] > d[cur.node] + 1) {
d[nextNode] = d[cur.node] + 1;
queue.add(new Node(cur.node + dx[i], d[cur.node] + 1));
}
}
}이 문제의 핵심 코드이다
방향벡터 -1,1,2를 모두 처리하기 위해 for문으로 감쌋고, 각 방향벡터별로 최단거리 배열의 인덱스를 보장하기 위해 if 문에 조건을 추가해줬다
(이전 비슷한 유형의 문제에서 인덱스 조건을 처리하지 않아서 계속 ArrayIndexOutOfBounds exception을 발생시켰던 경험이 있다)
만약 다음 노드의 최단거리보다 현재노드의 최단거리 + 소모시간 (0 or 1)이 더 작다면 이를 업데이트 해주고, 새로운 노드를 생성하여 큐에 담는다
최종 코드
public class Main {
static int[] dx = {-1, 1, 2};
static int[] d;
static int N, K;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
K = Integer.parseInt(st.nextToken());
d = new int[100_001];
dijkstra(N, K);
System.out.println(d[K]);
}
private static void dijkstra(int start, int end) {
PriorityQueue<Node> queue = new PriorityQueue<>();
Arrays.fill(d, Integer.MAX_VALUE);
d[start] = 0;
queue.add(new Node(start, 0));
while (!queue.isEmpty()) {
Node cur = queue.poll();
for (int i = 0; i < 3; i++) {
if ((i == 2) && (cur.node * dx[i] <= 100_000)) {
int nextNode = cur.node * dx[i];
if (d[nextNode] > d[cur.node] + 0) {
d[nextNode] = d[cur.node] + 0;
queue.add(new Node(cur.node * dx[i], d[cur.node] + 0));
}
} else if ((i == 0 || i == 1) && (0 <= cur.node + dx[i] && cur.node + dx[i] <= 100_000)) {
int nextNode = cur.node + dx[i];
if (d[nextNode] > d[cur.node] + 1) {
d[nextNode] = d[cur.node] + 1;
queue.add(new Node(cur.node + dx[i], d[cur.node] + 1));
}
}
}
}
}
static class Node implements Comparable<Node> {
int node;
int weight;
public Node(int node, int weight) {
this.node = node;
this.weight = weight;
}
@Override
public int compareTo(Node o) {
return this.weight - o.weight;
}
}
}풀이 후기
이전 숨바꼭질 문제는 가중치가 모두 1로 동일하고, 다음 방문 노드에 방문여부가 체크가 되어있으면, 최단 시간에 도착한 지점이므로 방문을 할 필요가 없었다.
하지만 이번 문제는 가중치(이동 비용)가 0(순간 이동)과 1(걷기)로 구분이 되어있으므로, 방문 여부와 상관 없이 다익스트라를 사용하여 최단 비을 갱신해야 한다
비용이 0과 1이므로 이를 간선의 가중치에 비유하여 다익스트라를 떠올릴 수 있나가 이 문제의 핵심 포인트 인 것 같다.
처음에 우선순위 큐를 사용하여 BFS를 구현하는것을 시작으로 방향벡터를 사용한 탐색 문제,
필수로 방문해야 하는 노드가 존재, 가중치가 다를 때 최단거리 구하기 등등 그래프의 다양한 문제를 접하고 풀이를 하다보니 점점 발전하는 것이 체감된다.
이제 위 문제들을 짬뽕한 수준의 문제는 거뜬히 풀 수 있다는 자신감이 생겼다 !