백준 Q1504 - 특정한 최단 경로

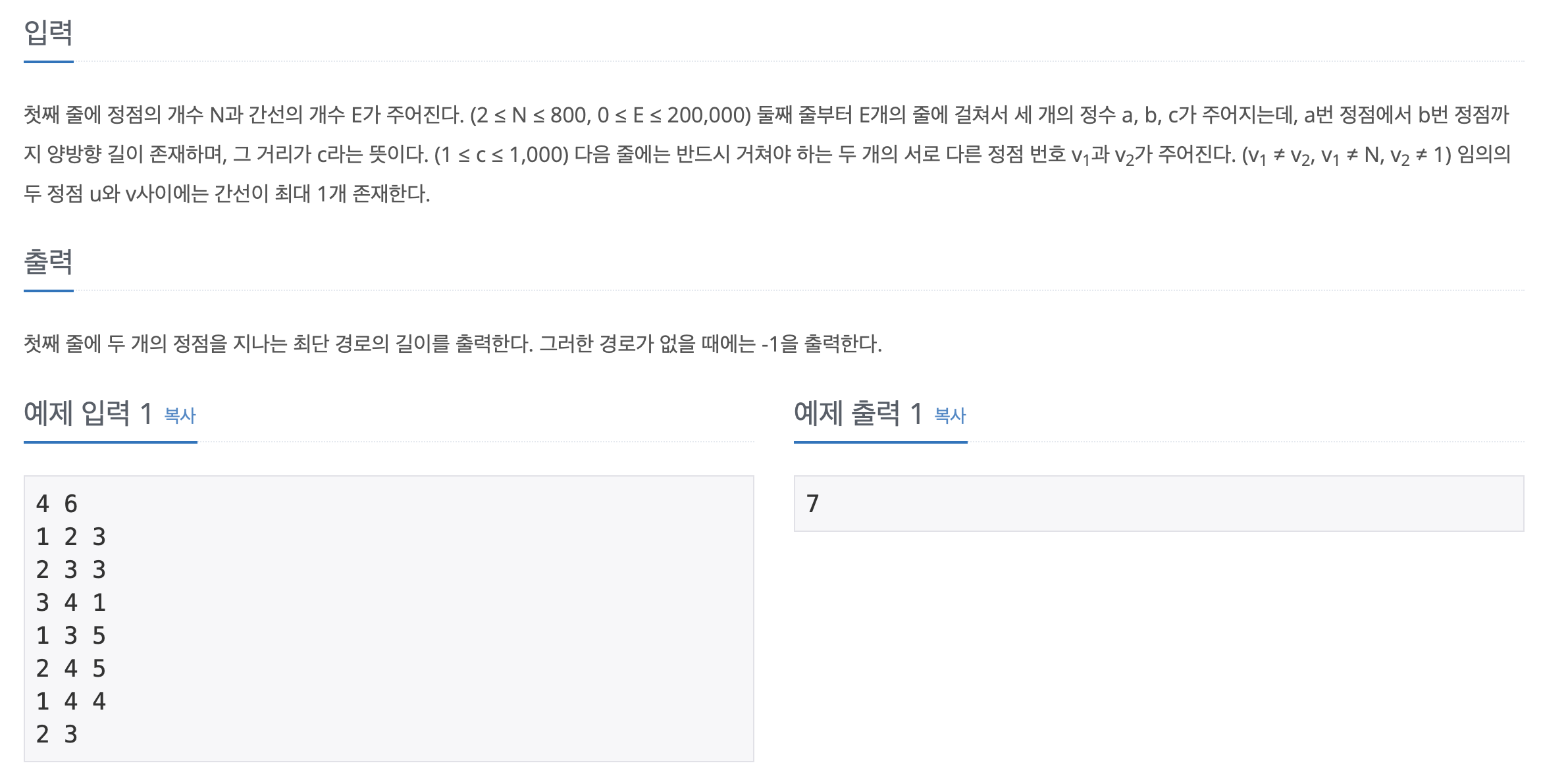
문제 및 입출력

---

풀이

그래프에서 최단 경로를 구하는 문제이므로 바로 다익스트라를 떠올렸다
이번 문제의 특징은 다음과 같다

1. 간선에 방향성이 존재하지 않는다
2. 임의로 주어진 두 정점을 반드시 통과해야 한다
3. 임의의 두 정점 사이에 간선이 최대 1개가 존재한다

위 특징들을 통해 뽑아낸 문제 풀이 방법은 다음과 같다
-> 간선에 방향성이 존재하지 않으므로 리스트형 배열에 추가할때 양방향으로 추가한다
-> 필수로 지나야 하는 두 정점 사이에 최단경로를 고려하여 방문 순서를 정한다
-> 두 정점사이에 간선이 최대 1개 이므로 연결되지 않은 정점들도 고려해야 한다

static int N, E;
static ArrayList<Node>[] graph;

최단거리를 비교해야 하므로 최단거리를 담는 배열은 정적 변수로 선언하지 않았다

graph[a].add(new Node(b, weight));
graph[b].add(new Node(a, weight));

양방향성을 띄므로 양쪽 정점 모두에 방향성을 만들어준다

int from1ToV1 = dijkstra(1, v1);
int fromV1ToV2 = dijkstra(v1, v2);
int fromV2ToN = dijkstra(v2, N);

int from1ToV2 = dijkstra(1, v2);
int fromV2ToV1 = dijkstra(v2, v1);
int fromV1ToN = dijkstra(v1, N);

start node는 1로 고정이고
start -> V1 -> V2 -> N
start -> V2 -> V1 -> N
두 방문 루트중 최적의 거리를 나타내는 루트를 구하기 위해 각각 다익스트라 함수를 돌려준다.

static int dijkstra(int start, int end) {
		...
        int[] d = new int[N + 1];
        ...
		queue.add(new Node(start, 0));

}

다익스트라 함수 코드는 여느때와 다름이 없지만, 해당 문제에서는 최단경로 비교를 하기 위해
최단 거리를 저장하는 배열을 다익스트라 알고리즘 안에 넣고,
시작 노드를 파라미터로 받아온 start로 생성자를 통해 객체를 만들었다

int route1 = (from1ToV1 == Integer.MAX_VALUE || fromV1ToV2 == Integer.MAX_VALUE 
					|| fromV2ToN == Integer.MAX_VALUE)
                ? Integer.MAX_VALUE
                : from1ToV1 + fromV1ToV2 + fromV2ToN;

int route2 = (from1ToV2 == Integer.MAX_VALUE || fromV2ToV1 == Integer.MAX_VALUE 
					|| fromV1ToN == Integer.MAX_VALUE)
                ? Integer.MAX_VALUE
                : from1ToV2 + fromV2ToV1 + fromV1ToN;

노드간에 간선이 존재하지 않을수도 있으므로, 셋 중 하나라도 간선이 없으면 초기최단 경로 값인 Integer.MAX_VALUE로 값을 저장한다

int minimumDistance = Math.min(route1, route2);
System.out.println(minimumDistance == Integer.MAX_VALUE ? -1 : minimumDistance);

이후 최단 경로를 구하고, 값이 Integer.MAX_VALUE로 간선이 존재하지 않는다면 문제에서 요구하는대로 -1을 출력하면 된다

---

최종 코드

public class Main {
    static int N, E;
    static ArrayList<Node>[] graph;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());

        N = Integer.parseInt(st.nextToken());
        E = Integer.parseInt(st.nextToken());

        graph = new ArrayList[N + 1];
        for (int i = 1; i <= N; i++) {
            graph[i] = new ArrayList<>();
        }

        for (int i = 0; i < E; i++) {
            st = new StringTokenizer(br.readLine());
            int a = Integer.parseInt(st.nextToken());
            int b = Integer.parseInt(st.nextToken());
            int weight = Integer.parseInt(st.nextToken());

            graph[a].add(new Node(b, weight));
            graph[b].add(new Node(a, weight));
        }

        st = new StringTokenizer(br.readLine());
        int v1 = Integer.parseInt(st.nextToken());
        int v2 = Integer.parseInt(st.nextToken());

        int from1ToV1 = dijkstra(1, v1);
        int fromV1ToV2 = dijkstra(v1, v2);
        int fromV2ToN = dijkstra(v2, N);

        int from1ToV2 = dijkstra(1, v2);
        int fromV2ToV1 = dijkstra(v2, v1);
        int fromV1ToN = dijkstra(v1, N);

        int route1 = (from1ToV1 == Integer.MAX_VALUE 
        				|| fromV1ToV2 == Integer.MAX_VALUE 
                        || fromV2ToN == Integer.MAX_VALUE)
                ? Integer.MAX_VALUE : from1ToV1 + fromV1ToV2 + fromV2ToN;

        int route2 = (from1ToV2 == Integer.MAX_VALUE 
        				|| fromV2ToV1 == Integer.MAX_VALUE 
                        || fromV1ToN == Integer.MAX_VALUE)
                ? Integer.MAX_VALUE : from1ToV2 + fromV2ToV1 + fromV1ToN;

        int minimumDistance = Math.min(route1, route2);

        System.out.println(minimumDistance == Integer.MAX_VALUE ? -1 : minimumDistance);
    }

    static int dijkstra(int start, int end) {
        PriorityQueue<Node> queue = new PriorityQueue<>();
        int[] d = new int[N + 1];
        for (int i = 1; i <= N; i++) {
            d[i] = Integer.MAX_VALUE;
        }
        queue.add(new Node(start, 0));
        d[start] = 0;

        while (!queue.isEmpty()) {
            Node cur = queue.poll();
            int node = cur.node;

            for (Node temp : graph[node]) {
                int nextNode = temp.node;
                int distance = temp.weight;

                if (d[nextNode] > d[node] + distance) {
                    d[nextNode] = d[node] + distance;
                    queue.add(new Node(nextNode, d[nextNode]));
                }
            }
        }

        return d[end];
    }

    static class Node implements Comparable<Node> {
        int node;
        int weight;

        public Node(int node, int weight) {
            this.node = node;
            this.weight = weight;
        }

        @Override
        public int compareTo(Node o) {
            return this.weight - o.weight;
        }
    }
}

---

풀이 후기

지금까지 방향성이 존재하는 그래프에서 단순히 최단경로를 구하는 문제만 풀어봤었다
다익스트라를 여러번 돌리기 위해 최단거리 배열을 다익스트라함수 안으로 할당하고, start를 매개변수로 받아서 노드를 생성하기 시작하고 큐에 담는것이 인상적이었다
두 정점을 지나기 필수로 위해 총 두가지 루트를 생각하는것은 어렵지 않았다

...
static final int INF = 200_000_000;
...
public static void main(String[] args) throws IOException {
	int route1 = dijkstra(1, v1) + dijkstra(v1, v2) + dijkstra(v2, N);
	int route2 = dijkstra(1, v2) + dijkstra(v2, v1) + dijkstra(v1, N);
	
    // route 값이 INF 보다 큰 것의 의미는, 세 경로 중 연결이 안된 노드가 하나 있다는 의미
	int minimumDistance = (route1 >= INF && route2 >= INF) 
							? -1 : Math.min(route1, route2);
...
}

static int dijkstra(int start, int end){
...
Arrays.fill(d, INF);
...
}

위와 같이 가독성이 좋게 수정하는것도 좋은 방법인 것 같다.