백준 Q1991 - 트리 순회

---

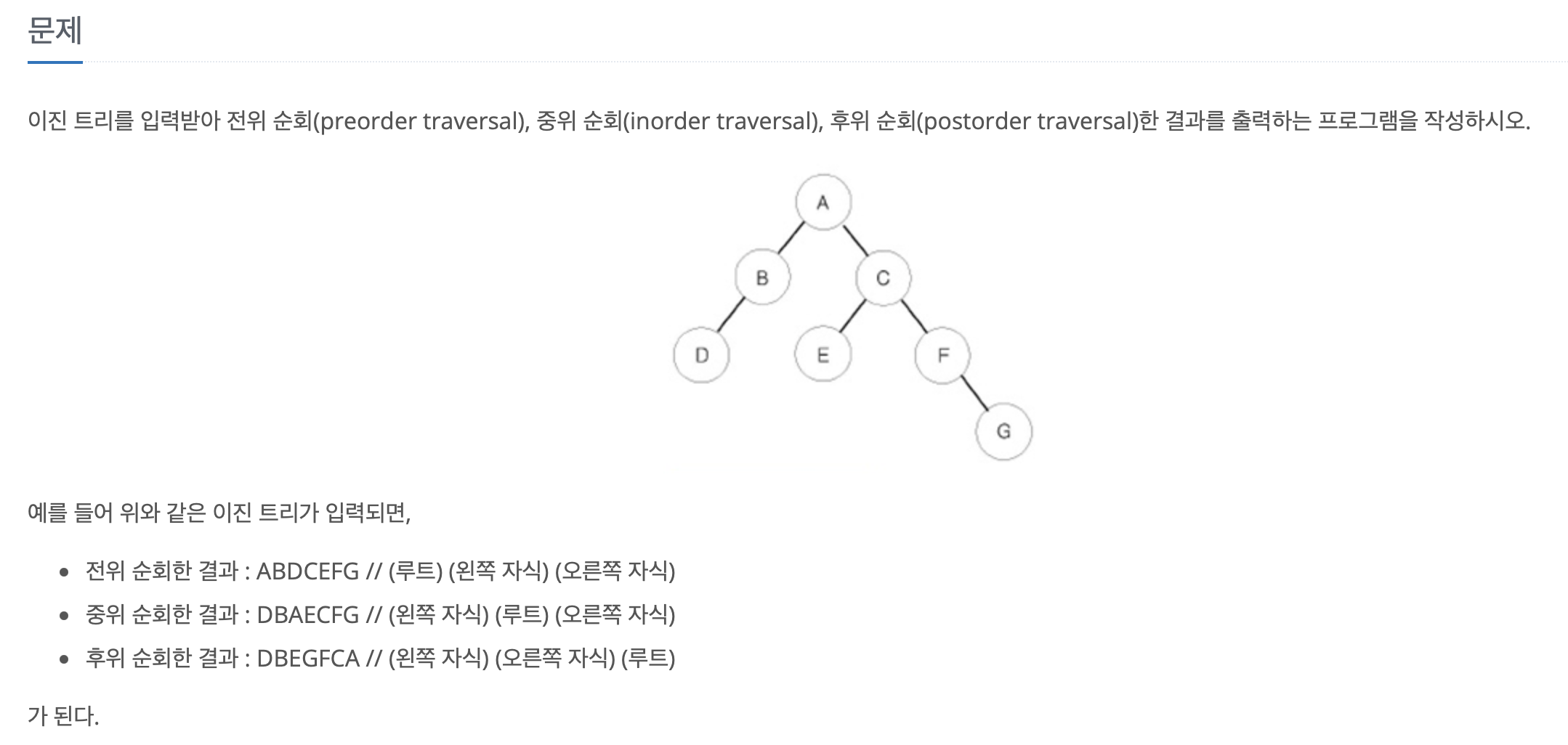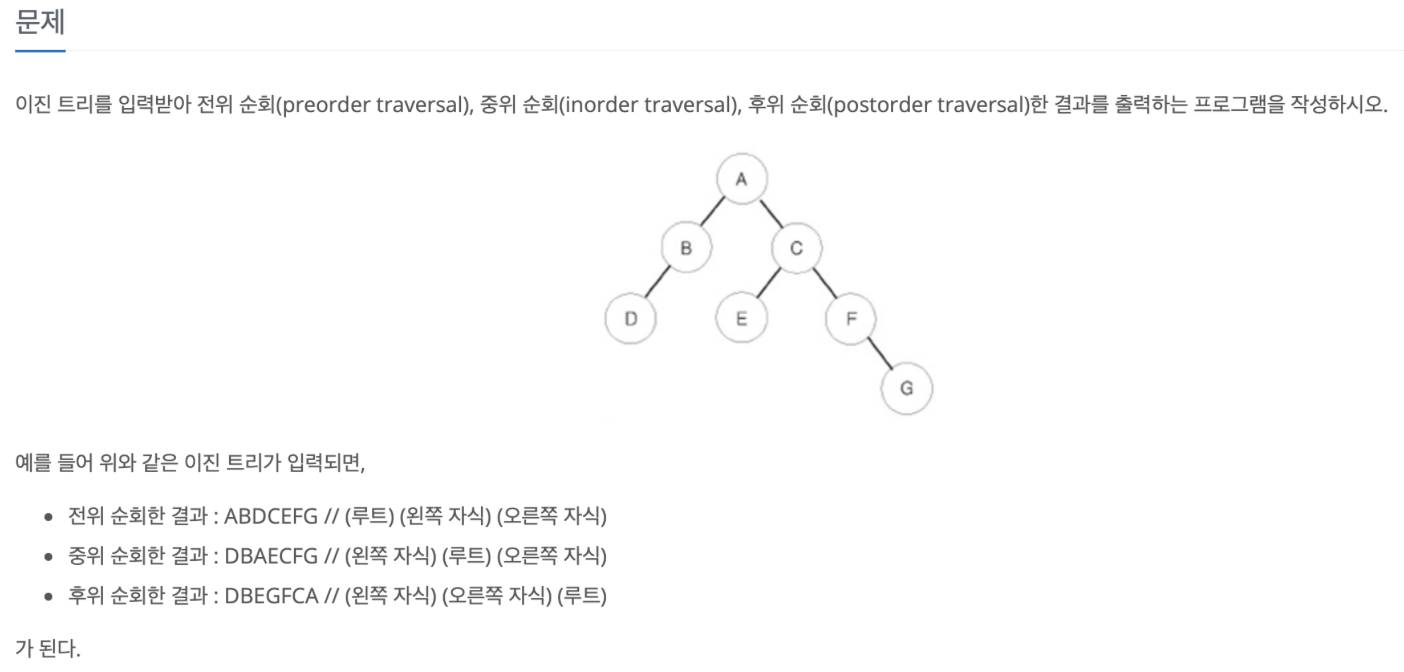
트리문제는 늘 하던대로 원소가 정수형 리스트인 배열을 선언하자

static ArrayList<Integer>[] tree = new ArrayList[26];

선언과 동시에 배열의 크기를 26으로 선언해줬는데, 이전 문제들은 노드에 정수값이 들어있었지만 이 문제는 알파벳 값이므로 A~Z 26개 만큼 선언해주자.

String[] nodes = br.readLine().split(" ");
int parent = nodes[0].charAt(0) - 'A';
char leftChild = nodes[1].charAt(0);
char rightChild = nodes[2].charAt(0);

한 줄씩 입력받아 부모노드와 좌,우 자식노드들을 각각 변수에 담아둔다
이때 부모노드의 인덱스를 정수형으로 파라미터를 넘겨서 재귀를 진행하기 위해 nodes[0].charAt(0) - 'A' 를 한 것을 볼 수 있다.
nodes[0].charAt(0) 의 값은 Character 값인 A 인데, 배열의 크기를 26으로 지정했으므로 A~Z 를 숫자 0~25값으로 변환하기 위해 위해 -A 를 해주었다.

if (leftChild == '.') {
	tree[parent].add(-1);
} else {
	tree[parent].add(leftChild - 'A');
}

if (rightChild == '.') {
	tree[parent].add(-1);
} else {
	tree[parent].add(rightChild - 'A');
}

문제의 입력에서 자식노드가 없는경우 . 으로 표기를 하므로 해당 상황에서는 편리하게 정수 -1 로 처리한다

private static void preOrder(int current) {
	if (current == -1) {
		return;
	}
	System.out.print((char) (current + 'A'));
	preOrder(tree[current].get(0));
	preOrder(tree[current].get(1));
}

각각의 순회는 재귀를 통해 진행하고, basecase 는 자식이 없는 상태인 -1 값일 경우 이다.
전위순회 코드와 동일한 논리로 중위순회와 후위순회 로직을 구현하면 된다.

---

최종 코드

class Main {
    static int N;
    static ArrayList<Integer>[] tree = new ArrayList[26];

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        N = Integer.parseInt(br.readLine());

        for (int i = 0; i < 26; i++) {
            tree[i] = new ArrayList<>();
        }

        for (int i = 0; i < N; i++) {
            String[] nodes = br.readLine().split(" ");
            int parent = nodes[0].charAt(0) - 'A';
            char leftChild = nodes[1].charAt(0);
            char rightChild = nodes[2].charAt(0);

            if (leftChild == '.') {
                tree[parent].add(-1);
            } else {
                tree[parent].add(leftChild - 'A');
            }

            if (rightChild == '.') {
                tree[parent].add(-1);
            } else {
                tree[parent].add(rightChild - 'A');
            }
        }
        preOrder(0);
        System.out.println();
        inOrder(0);
        System.out.println();
        postOrder(0);
        System.out.println();
    }

    private static void preOrder(int current) {
        if (current == -1) {
            return;
        }
        System.out.print((char) (current + 'A'));
        preOrder(tree[current].get(0));
        preOrder(tree[current].get(1));
    }

    private static void inOrder(int current) {
        if (current == -1) {
            return;
        }
        inOrder(tree[current].get(0));
        System.out.print((char) (current + 'A'));
        inOrder(tree[current].get(1));
    }

    private static void postOrder(int current) {
        if (current == -1) {
            return;
        }
        postOrder(tree[current].get(0));
        postOrder(tree[current].get(1));
        System.out.print((char) (current + 'A'));
    }
}

---

풀이 후기

다른분들의 풀이를 찾아보니 리스트형 배열이 아닌, 2차원 배열로 구현하신 분들을 많이 볼 수 있었다. 나는 지금까지 트리문제 푸는 방식으로 푸는게 편해서 리스트형 배열로 풀이를 하였다.
문제마다 그림을 그려 완벽히 이해하고 넘어가고자 하는 타입인데, 이 문제를 풀며 손으로 그려보다 궁금점이 생겼다.
트리는 사이클이 존재하지 않는 그래프인데 그럼 트리 구조 한정으로 전위 순회와 깊이우선탐색(DFS)는 같은 것인가? => 맞다

• DFS와 BFS는 그래프와 트리구조에서 탐색하는 알고리즘
• 전위순회, 중위순회, 후위순회는 사이클이 존재하지 않는 특성을 가진 트리 구조에서 각 노드를 방문하는 알고리즘

따라서 트리는 순회가 없으므로 각 노드별로 방문여부를 확인할 필요가 없고, 재귀를 사용하여 구현 하는것이 적합하다.
그래프는 사이클이 존재하기 때문에 방문여부를 확인해야하므로 재귀는 적합하지 않고, 연결리스트를 활용한 큐를 구현하는 것이 적합하다.

(24.11.18 정정 )
통상 DFS는 재귀 BFS는 큐로 구현