백준 Q2263 - 트리의 순회

트리를 탐색하는 문제만 풀다가 트리가 주어지지 않고 순회 결과가 주어진 문제는 처음 접해봤다.

루트노드를 언제 방문하느냐에 따라서 다음과 같은 순회가 존재한다

• 전위 순회(프리오더): 루트 노드 -> 왼쪽 자식노드 -> 오른쪽 자식노드
• 중위 순회(인오더): 왼쪽 자식노드 -> 루트 노드 -> 오른쪽 자식노드
• 후위 순회(포스트 오더): 왼쪽 자식노드 -> 오른쪽 자식노드 -> 루트노드

해당 문제에서는 중위 순회와 후위 순회의 결과를 통해 무엇을 파악할 수 있느냐가 문제를 풀기위한 가장 중요한 키이다.

후위순회는 항상 가장 마지막 방문하는 노드가 루트노드이다.
그렇다면 중위 순회의 중앙값은 항상 루트 노드일까? 라고 생각하면 문제를 풀지 못할 것이다.

완전 이진트리가 아니기 때문에 루트 노드 기준으로 왼쪽 서브트리와 오른쪽 서브트리가 대칭이 아닐 수도 있다.
내가 생각했던 이진트리의 개념은 완전 이진트리가 아니고 포화 이진트리였다

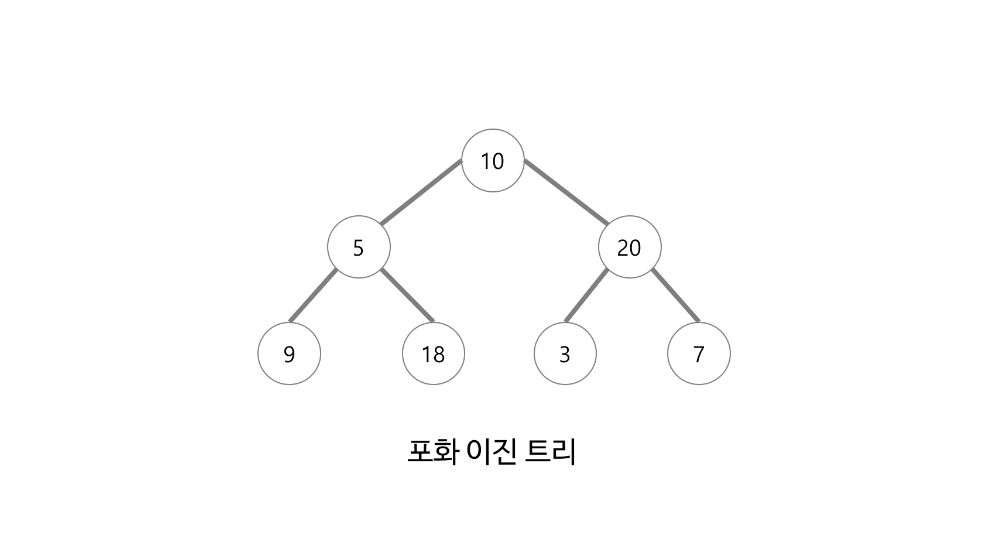
포화 이진 트리(飽和二進-, 영어: perfect binary tree)는 모든 내부 노드가 두 개의 자식 노드를 가지며 모든 잎 노드가 동일한 깊이 또는 레벨을 갖는다(이는 애매모호하게 완전 이진 트리라고도 불린다).

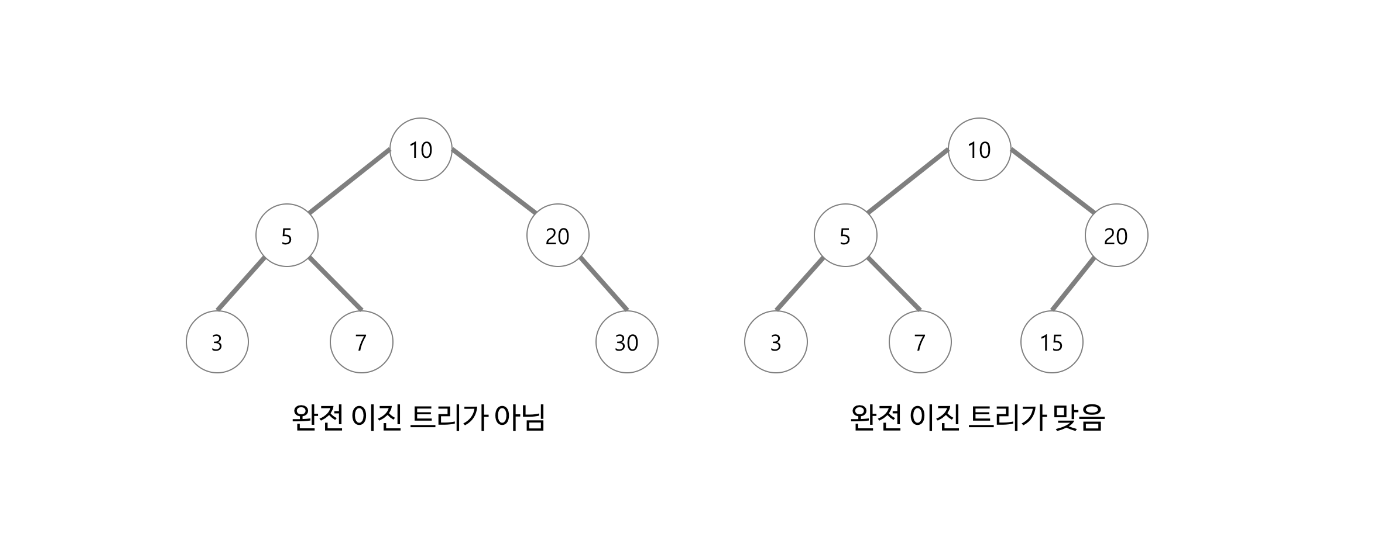
완전 이진 트리(完全二進-, 영어: complete binary tree)에서, 마지막 레벨을 제외하고 모든 레벨이 완전히 채워져 있으며, 마지막 레벨의 모든 노드는 가능한 한 가장 왼쪽에 있다.

아무튼 이 문제에서 포화 이진트리가 아니므로 중위순회의 중앙값이 루트라는 값을 보장할 수 없다.
후위순회의 마지막 값(현 시점의 루트값)을 통해 중위순회에서의 rootIdx 를 찾을 수 있다

int rootNode = postOrder[pe];
int rootIdx = getRootIdx(rootNode);

private static int getRootIdx(int rootNode) {
    for (int i = 0; i < inOrder.length; i++) {
        if (inOrder[i] == rootNode) {
            return i;
        }
    }
    return -1;
}

이렇게 찾은 루트값을 통해 중위순회의 결과값에서 루트를 기준으로 왼쪽 서브트리 오른쪽 서브트리를 파악할 수 있다.
또한 주어진 문제에서 비슷한 구조의 더 작은 문제로 나눌 수 있으므로 바로 재귀를 떠올렸다.
루트값이 매 재귀마다 바뀌며 트리의 왼쪽 서브트리와 오른쪽 서브트리 또한 바뀌므로 파라미터값을 적절히 채워주는것이 중요하다

private static void getPreOrder(int is, int ie, int ps, int pe) {
    if (is > ie || ps > pe) {
        return;
    }
    preOrder[idx++] = postOrder[pe];
    int rootNode = postOrder[pe];
    int rootIdx = getRootIdx(rootNode);

    getPreOrder(is, rootIdx - 1, ps, ps + rootIdx - is - 1);
    getPreOrder(rootIdx + 1, ie, ps + rootIdx - is, pe - 1);
}

변수 설명

• is, ie: inOrder start index , inOrder end index
• ps, pe: postOrder start index, postOrder end index

첫 번째 재귀는 왼쪽 서브트리를 탐색하며 루트값을 저장,
두 번째 재귀는 오른쪽 서브트리를 탐색하며 루트값을 저장하는 재귀식이다.

위 식에서 가장 중요한 것은 왼쪽 서브트리의 노드의 개수 이다
중위 순회값에서 rootIdx - is 를 하면 왼쪽 서브트리의 노드의 개수를 구할 수 있다.
해당 식을 각 서브트리의 탐색마다 적절히 가공하여 파라미터를 채워주면 된다.

최종 코드

public class Main {
    static int[] preOrder, inOrder, postOrder;
    static BufferedReader br;
    static int N;
    static int idx = 0;

    public static void main(String[] args) throws IOException {
        br = new BufferedReader(new InputStreamReader(System.in));
        N = Integer.parseInt(br.readLine()); //정점의 개수

        preOrder = new int[N];
        inOrder = getOrder();
        postOrder = getOrder();
        getPreOrder(0, N - 1, 0, N - 1);

        for (int i : preOrder) {
            System.out.print(i + " ");
        }
    }

    private static void getPreOrder(int is, int ie, int ps, int pe) {
        if (is > ie || ps > pe) {
            return;
        }
        preOrder[idx++] = postOrder[pe];
        int rootNode = postOrder[pe];
        int rootIdx = getRootIdx(rootNode);

        getPreOrder(is, rootIdx - 1, ps, ps + rootIdx - is - 1);
        getPreOrder(rootIdx + 1, ie, ps + rootIdx - is, pe - 1);
    }

    private static int getRootIdx(int rootNode) {
        for (int i = 0; i < inOrder.length; i++) {
            if (inOrder[i] == rootNode) {
                return i;
            }
        }
        return -1;
    }

    private static int[] getOrder() throws IOException {
        StringTokenizer st = new StringTokenizer(br.readLine());
        int[] temp = new int[N];
        for (int i = 0; i < N; i++) {
            temp[i] = Integer.parseInt(st.nextToken());
        }
        return temp;
    }
}

풀이 후기

오랜만에 트리와 재귀를 접목시킨 난이도가 꽤 있는 문제를 풀어보니 아직 재귀에 익숙하지 않다는 것을 다시 느끼게 되었다. 트리는 자료구조 공부를 열심히 했기 때문에 금방 복기할 수 있었는데, 재귀는 문제를 더 많이 풀며 적응을 해야할 것 같다고 생각한다.