머신러닝

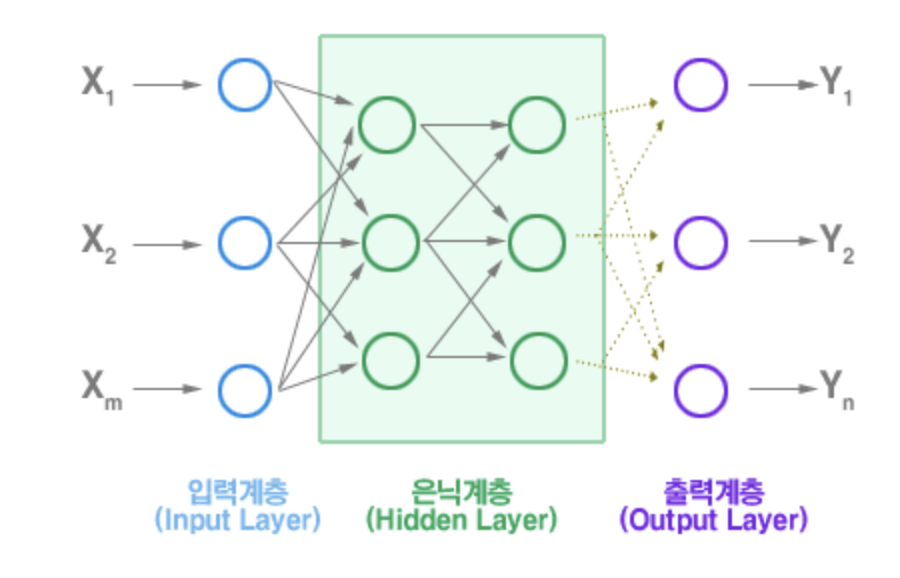
단층 퍼셉트론

• 입력층과 출력층을 가진다 --> 입력층은 계산을 하지 않으므로 퍼셉트론은 단층 구조로 간주한다.
• 입력층의 i번째 노드는 특징 벡터 x=(x1, x2, ... , xd)T의 요소로 xi를 담당
• i번째 입력 노드와 출력 노드를 연결하는 에지는 가중치 wi를 가진다.
  
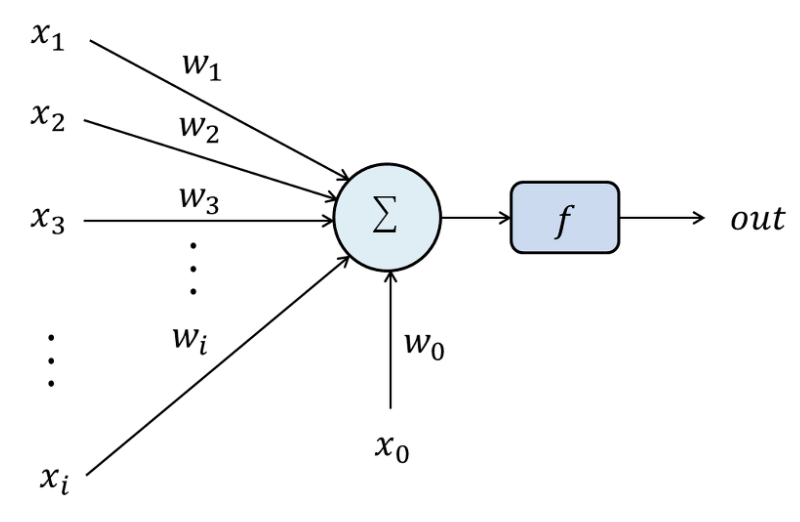
• 퍼셉트론의 동작은 특징값과 가중치를 서로 곱하고 더하여 s를 구하고 이를 활성화 함수 A에 적용한다.
• 활성화 함수 A는 계단 함수를 사용한다.
• 퍼셉트론에서 선형결합된 값은 직선을 이루며 이를 결정직선이라고 한다.
• 결정 직선은 전체 공간을 +1과 -1의 두 부분 공간으로 분학하는 분류기 역할을 한다.
• 2차원에서는 결정직선, 3차원은 결정 편면, 4차원 이상은 결정 초평면이있다.
• 목적 함수는 항상 0보다 큰 값을 주며, w가 최적이면 즉 모든 샘플을 맞춘다면 출력은 0이 된다. 즉 많이 틀리면 목적 함수는 큰 값을 가진다.

다층 퍼셉트론

• 퍼셉트론은 하나의 직선을 이루지만 이는 2개의 부류로 정확히 분류할 수 없는경우가 있다(ex.XOR)
  

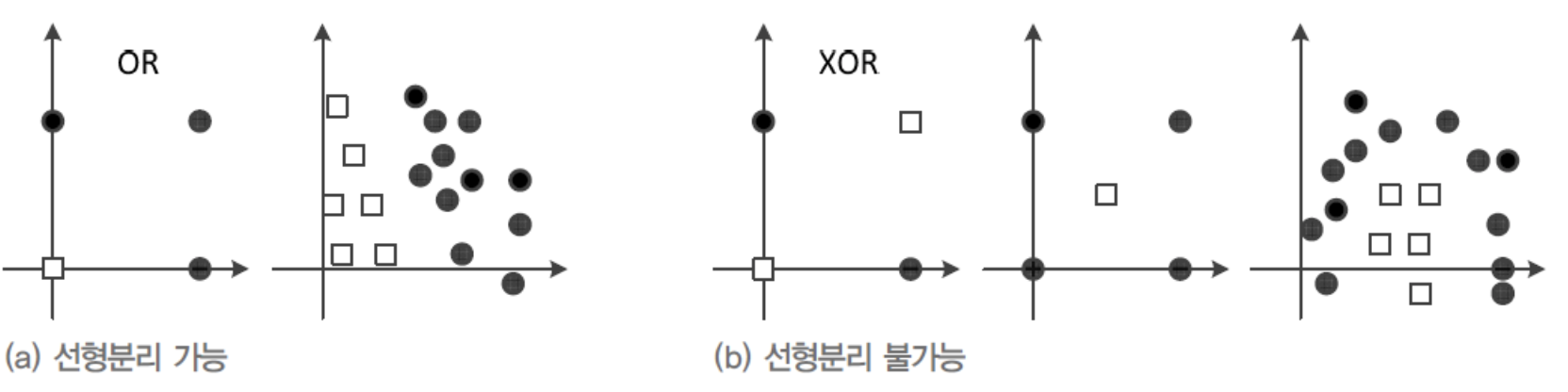
• 이를 해결하기 위해 퍼셉트론을 여러개 연결한 다층 퍼셉트론을 사용한다

• 다층 페셉트론의 핵심사항
  1. 은닉층을 사용하여 특징 공간을 분류하는데 유리한 새로운 특징 공간으로 변환한다.
  2. 시그모이드 활성 함수를 도입하여 출력을 신뢰도로 간주하여 더욱 융통성 있는 의사결정을 할 수 있다.
  3. 오류 역전파 알고리즘을 사용한다(그라디언트를 계산하여 가중치 갱신).

• 퍼셉트론 2개를 사용한 경우
  

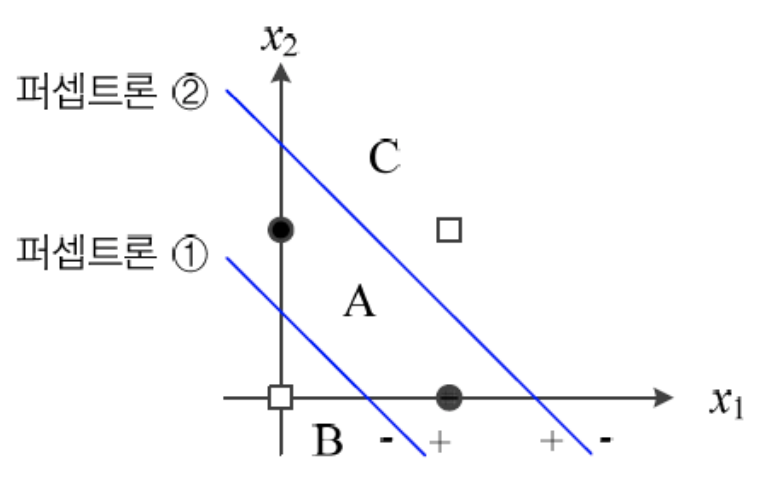
• 퍼셉트론 2개를 병렬로 연결한 경우
  

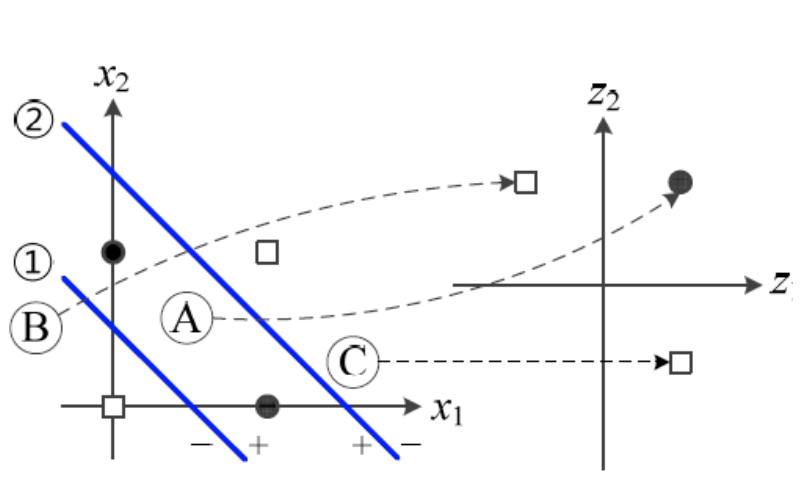
• 2개의 병렬 후 1개의 퍼셉트론이 더 연결된다면 이는 변환된 공간을 다시 직선이 2부류로 나눈다.

• 은닉층은 특징 벡터를 분류에 더 유리한 새로운 특징 공간으로 변환하며 특징 학습이라고 부른다.