Deep ML. Loss Functions (손실함수)

지난 포스팅에서 Linear Classifier는 parametric classifier의 일종이며, parametric classifier 라는 것은 training data의 정보가 파라미터인 '행렬 W'로 요약된다는 것을 뜻하고, W가 학습되는 것이라 배웠다.

이런식으로 알고리즘을 만들고 어떤 W가 가장 좋은지를 결정하기 위해서는 지금 만든 W가 좋은지 나쁜지를 살펴봐야 한다. 그래서 우리가 해줘야할 일은 다음과 같다.

[TODO]

• Define a loss function that quantifies our unhappiness with the scores across the training data.
  임의의 W값이 얼마나 좋은지 나쁜지 정량화 해줘야한다.
• Come up with a way of efficiently finding the parameters that minimize the loss function.(Optimization) : 수많은 W중 "가장 덜 구린" W를 찾는다.

W를 입력으로 받아서 각 스코어를 확인하고 이 W가 지금 얼마나 거지같은지를 정량적으로 말해주는 것이 손실함수(Loss Function)이다.

Multiclass SVM loss

첫번째 Loss function은 Multiclass SVM이다. 여러 클래스를 다루기 위해 이진(단일) SVM의 일반화된 형태이다.
SVM loss의 식은 밑에와 같다.

$L_i$를 구하기 위해 우선 올바른(correct) 카테고리를 제외한 나머지(incorrect) 카테고리 y의 합을 구한다. 맞지 않는 카테고리를 전부 합치는 것이다. 그리고 올바른 카테고리와 그렇지 않은 카테고리의 스코어를 비교해본다.
만약 올바른 카테고리의 점수가 그렇지 않은 카테고리의 점수보다 더 높으면, 그 격차가 일정 마진(safty margin)이상이라면 (위 식에서는 마진을 1로 뒀다), 이 경우는 올바른 카테고리의 스코어가 다른 카테고리의 스코어보다 훨씬 더 크다는 것을 의미한다.
그렇게 되면 Loss는 0이 된다.
*margin에 대해 궁금하다면?*

이미지 내 정답이 아닌 카테고리의 모든 값들을 합치면, 그 값이 바로 한 이미지의 최종 Loss가 되는 것이다. 그리고 전체 트레이닝 데이터 셋에서 그 Loss들의 평균을 구한다.
수식화 시켜서 if-then으로 표현해보자면, if 정답 클래스의 스코어 점수가 제일 높으면 then $max(0, s_j - {s_y}_i + 1)$

아래와 같이 3개의 클래스를 가진 학습(training) 데이터가 있다고 치자.

아래의 그래프는 Hinge Loss이다. $x$축은 ${s_y}_i$이며 정답 클래스의 점수이다. $y$축은 Loss값이다. 정답 카테고리의 점수가 올라갈수록 Loss가 선형적으로 줄어드는 것을 볼 수 있으며, Loss가 0이 됬다는 건 클래스를 잘 분류했다는 뜻이다.

손실 함수에서 $s$는 classifier의 출력으로 나온 예측된 스코어 이며, $y_i$는 이미지의 실제 정답 카테고리이며, ${s_y}_i$는 트레이닝 셋의 $i$번째 이미지의 정답 클래스의 스코어이다. Loss가 말하고자 하는 것은 정답 스코어가 다른 스코어들보다 높다면 좋다는 것이다.
정답 스코어는 safty margin(여기 예제에선 1)을 두고 다른 스코어들 보다 훨씬 더 높아야 한다. 충분히 높지 않으면 Loss가 높아지게 된다.

Loss가 어떻게 구해지는지 과정을 살펴보자.

1. 정답이 아닌 클래스를 순회한다. 첫번째 이미지는 cat이 정답이니 제낀다.
오른쪽은 각 카테고리로 도출된 스코어를 Loss function으로 넣어 해당 이미지의 Loss값을 구한다. 나온 Loss값은 "얼마나 분류기가 이 이미지를 후지게(?) 분류하는지"에 대한 척도이다.
2. car 이미지도 1.과 같은 작업을 행한다.
3. frog 이미지도 1.과 같은 작업을 행한다.
4. 전체 이미지에 대한 Loss값의 평균을 구해주면, 마지막 최종 Loss값이 나온다.

[학생의 질문]

Q. "1을 더하는 것"은 어떻게 결정하는가? (safty margin)
A. 우리가 궁금해하는 것은 Loss의 절대적 수치가 아니라, 여러 스코어 간의 상대적인 차이다. 우리가 관심있어 하는 건 오로지 정답 스코어가 다른 스코어에 비해 얼마나 더 큰 스코어를 가지고 있는지 이다.

[교수님 질문]

Q1. What happens to loss if car scores change a bit?
만약 car의 스코어를 조금 변하면 Loss는 어떻게 될까?
A1. Loss는 바뀌지 않을 것. SVM loss를 상기해보면 Loss는 오직 정답 스코어와 그 외의 스코어와의 차이만을 고려했다. 따라서 이 경우에는 Car의 스코어가 이미 다른 스코어들보다 엄청 높기 때문에 여기 스코어를 조금 바꾼다고 해도, 서로 간격(margin)은 여전히 유지될 것이며, 결국 Loss는 변하지 않는다. 즉, 계속 0이다.

Q2. What is the min/max possible loss?
SVM loss가 가질 수 있는 최소/최대값은 어떻게 될까?
A2. min: 0, max: infinite

Q3. At initalization W is small so all S $\approx$ 0. What is the loss?
모든 스코어 s가 "0에 가깝고", "값이 서로 비슷하다면" Multiclass SVM에서 loss가 어떻게 될까?
A3. number of classes - 1. 왜냐면 Loss를 계산할 때 정답이 아닌 클래스를 순회한다. 그러면 C(classes) - 1 클래스를 순회한다. 비교하는 두 스코어가 거의 비슷하니 margin 때문에 1 스코어를 얻을 것이다.
이 개념은 "디버깅 전략"으로 유용하다. 다시말해 트레이닝을 처음 시작할때 Loss C-1이 아니라면, 버그가 있다는 뜻이고 고쳐야 된다는 의미가 되기 때문이다.

Q4. What if the sum was over all classes?(including $j = y_i$)
SVM loss는 정답인 클래스는 빼고 다 더했다. 그렇다면 정답도 같이 더하면 어떻게 될까?
A4. Loss에 1이 증가한다. 우리가 정답 클래스만 빼고 계산하는 이유는, 일반적으로 loss가 0이 되어야지만 "아무것도 잃는 것이 없다"라고 쉽게 해석할 수 있기 때문이다.

Q5. What if we used mean instead of sum?
loss에서 전체 합을 쓰는게 아니라 평균을 쓰면 어떻게 될까?
A5. 영향을 미치지 않는다.
클래스의 수는 어차피 정해져있으니, 평균을 취하는건 그저 loss function을 rescale할 뿐이다. 스코어 값이 몇인지는 신경쓰지 않는다.

Q6. What if we used $L_i = \sum_{j\ne y_i} max(0, s_j - {s_y}_i + 1)^2$
손실함수를 제곱항으로 바꾸면 어떻게 될까?
A6. 결과가 달라질 것이다. (왜요?..... 대체... 왜?)

Multiclass SVM loss 수식 $L_i = \sum_{j\ne y_i} max(0, s_j - {s_y}_i + 1)$를 python코드로 표현하면 아래와 같다.

def L_i_vectorized(x, y, W):
  scores = W.dot(x)
  margins = np.maximum(0, scores - scores[y] + 1)
  margins[y] = 0
  loss_i = np.sum(margins)
  return loss_i

[여기서 질문]
Q. Loss가 0이 되게하는 W가 유일하게 하나만 존재하는 것일까?
A. 다른 W도 존재한다.
W의 스케일은 변하겠지반, W에 2배를 한다고 해도 loss는 여전히 0일 것이다.

좀더 좋은 W를 찾아야하지만, 다양한 W중 Loss가 0인 것을 선택하는 것은 모순이다.
loss function은 classifier에게 어떤 W를 찾고 있고, 어떤 W에만 신경쓰고 있는지를 말해주는 것이라면 조금 이상하다.
여기에서는 오직 데이터의 Loss에 대해서만 신경쓰고 있고, classifier에게 트레이닝 데이터에 꼭 맞는 W를 찾으라고 말하는 것과 같다. 하지만 실제로 우리는 트레이닝 데이터에 얼마나 꼭 맞는지 전혀 신경쓰지 않고있다.
기계학습의 핵심은 트레이닝 데이터를 이용해서 어떤 classifier를 찾는 것인데, 그 classifier는 테스트 데이터에 적용될 것이다.
고로, 우리가 관심 있어야 할 것은 트레이닝 데이터의 성능이 아니라, 테스트 데이터에서의 성능쪽으로 중심을 둬야 할 것이다. 그러니 classifier에게 트레이닝 데이터의 loss에만 신경쓰라고 한다면 좋지 않은 상황이 벌어질 것이다.

조금 더 다른 예를 들어보자면, 지금의 예는 지금까지 배웠던 linear classifier에 대한 것이 아니고 기계학습에서 다루는 좀더 일반적인 개념이라고 보면 된다.

밑에 그래프를 보면 파란색 점이 있는 데이터 셋이 있다고 해보자. 우리가 할일은 어떤 선을 가지고 파란색 점들에 fitting 시키는 것이다.

우리의 classifier에게 파란색 점들에 꼭 맞게 곡선을 그리라고 할테지만, 이런 상황은 "성능"을 전혀 고려하지 않았기 때문에 좋은 아이디어는 아니다.
우린 항상 테스트 데이터에서의 성능을 고려해야한다.

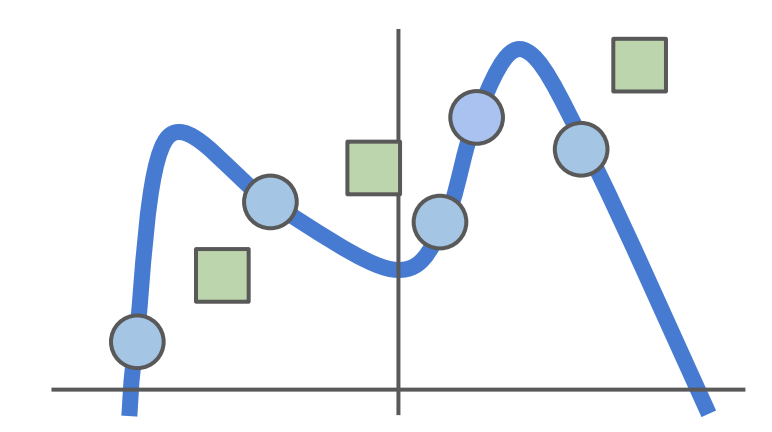
초록색 네모와 같은 새로운 데이터가 들어오면 앞서 만든 곡선은 완전히 틀리게 된다.
사실상 의도했던 선은 초록색 직선이며, 완벽하게 트레이닝 데이터에 꼭 맞는 복잡하고 구불구불한 곡선을 원한 것이 아니다. 이는 기계학습에서 가장 중요한! 문제이다!!

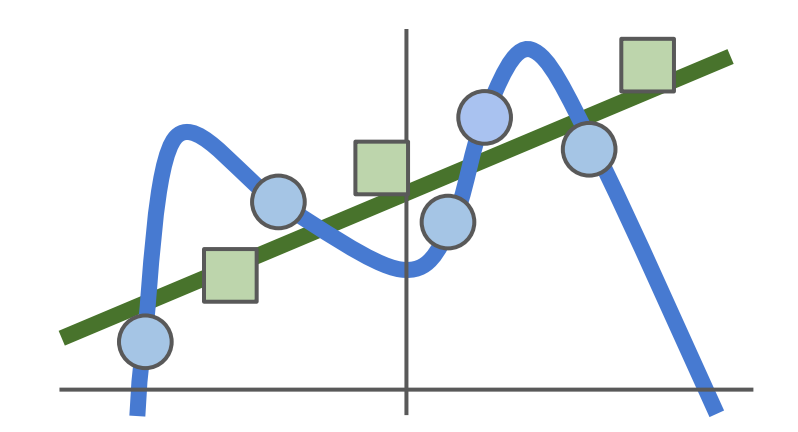
위와 같은 복잡함을 Model이 좀 더 단순한 W를 선택하도록 도와주는 역할을 하는 것이 Regularization이다.