BST(Binary Search Tree)는 어떤 자료구조일까?

Binary Search Tree는 그 이름 그대로 탐색에 최적화 되어있는 자료구조이다.

이진탐색트리(Binary Search Tree)는 각 노드의 값 보다 작은 값은 왼쪽 서브트리에, 각 노드의 값 보다 큰 값은 오른쪽 서브트리에 저장하는 정렬된 이진 트리 자료구조이다.

이진탐색트리는 힙(Heap)과 마찬가지로 새로운 데이터 삽입과 동시에 정해진 규칙에 맞게 정렬을 한다.

이진탐색트리의 시간복잡도는 검색, 삽입, 삭제 모두 O(logN) 이고, 최악의 경우 한 쪽으로 치우친 트리가 됐을때 O(N) 이 된다.

BST의 특징

정렬된 이진트리

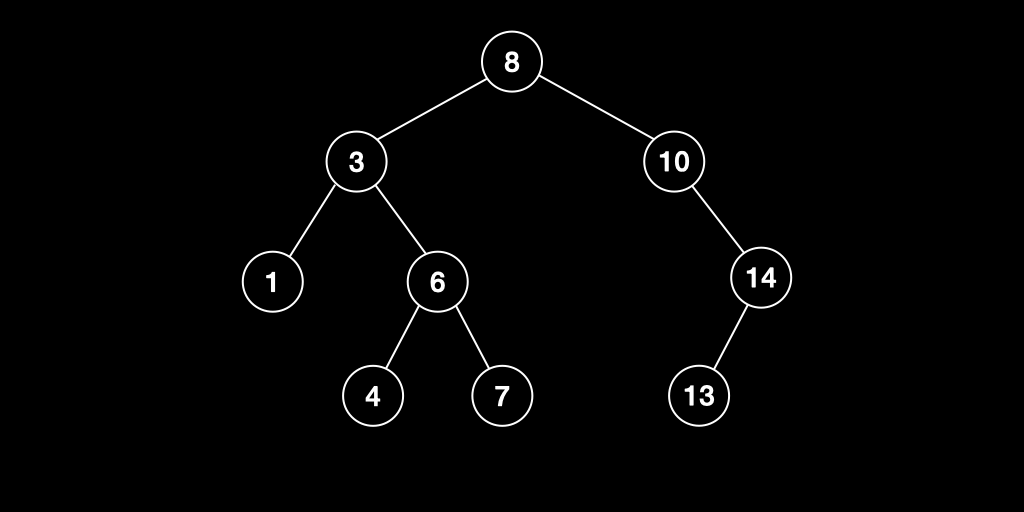
정렬된 이진트리인 이진탐색트리는 아래와 같은 조건을 만족한다.

1. 루트노드의 값보다 작은 값은 왼쪽 서브트리에, 큰 값은 오른쪽 서브트리에 있다.
2. [Recursive] 각각의 서브트리도 1번 조건을 만족한다.

정렬된 이진트리라는 점에서 힙과 헷갈릴수도 있다. 하지만 BST와 힙은 구조적으로나 논리적으로나 다른 모습을 하고 있다.
구조적으로는 BST는 어떠한 모양의 이진트리여도 상관 없지만, 힙은 완전이진트리 구조를 전제로 한다. 논리적으로는 BST의 경우 특정 노드를 기준으로 좌/우 서브트리에 적재되는 데이터가 모두 작거나 커야한다. 반면에, 힙의 경우 최소힙, 최대 힙이 있어 특정 노드를 기준으로 자식노드보다 작거나 커야한다.

중복값이 없음

기본적으로 이진탐색트리는 중복값을 허용하지 않는다. 그 이유는 자료구조의 효율성을 보장하기 위해서 인데 만약 중복값을 허용하게 된다면 아래와 같이 두 가지 검색 알고리즘이 나올 수 있다.
첫번째로, 검색하는 데이터 발견시 중단하는 방법이다. 이 알고리즘은 검색 자체의 효율성은 우수하지만 하위 노드에 불필요한 중복 데이터가 존재할 수 있어 공간적으로 비효율 적이다.
두번째로, 중복되는 모든 하위 노드를 다 검색하는 방법이다. 이 경우는 당연히 검색 효율이 좋지 않고, 중복값을 왼쪽 또는 오른쪽으로 모은다고 해도 비효율적일 수 밖에 없다.
따라서 이진탐색트리는 효율성을 위해 중복값을 허용하지 않는다.

BST의 연산

검색(Search)

이진탐색트리에서 특정 데이터를 찾는 과정은 다음과 같다.

1. 검색 값을 root와 비교한다.
2. 검색 값이 해당 노드의 값보다 작으면 왼쪽 자식노드와, 크면 오른쪽 자식노드와 비교한다.
3. 검색 값을 찾을때 까지 2번 작업을 반복한다.
4. 리프노트까지 도달 후 일치하는 값이 없으면 null을 반환한다.

삽입(Insertion)

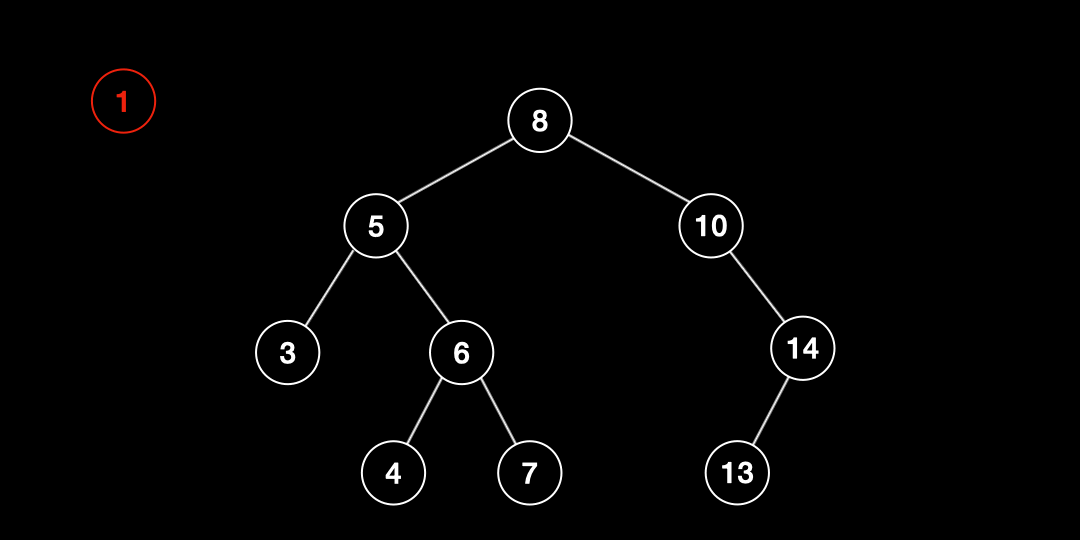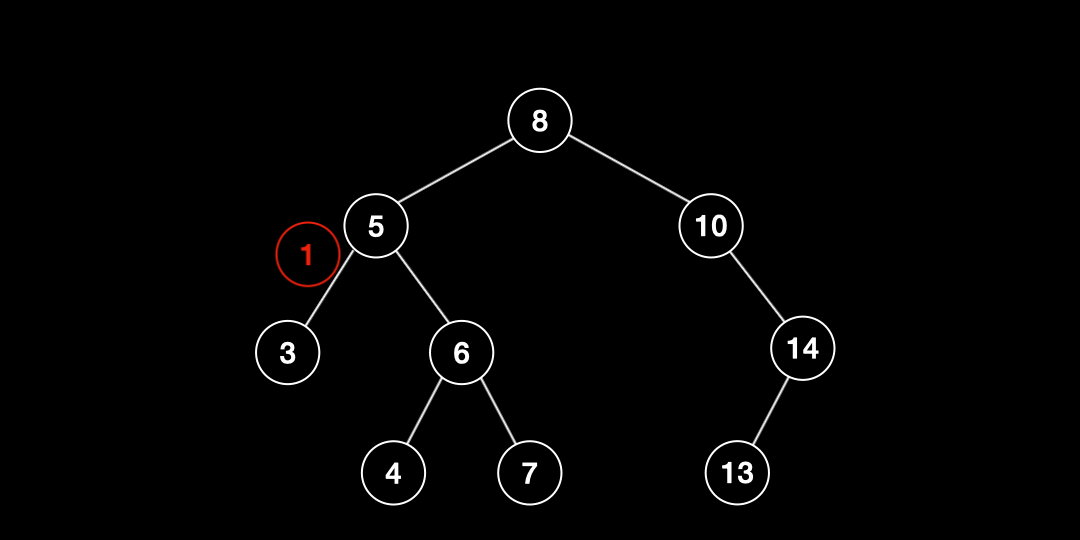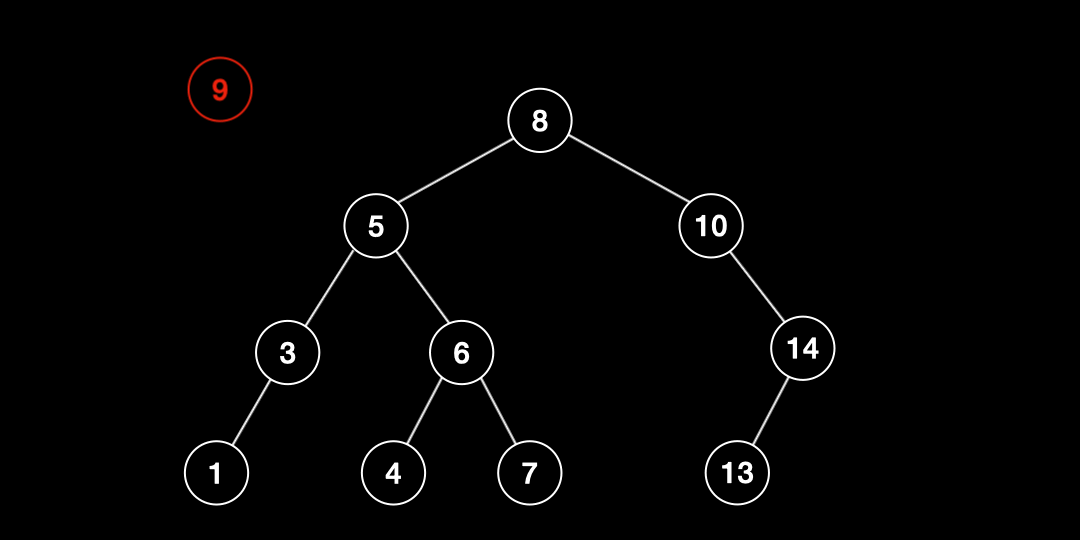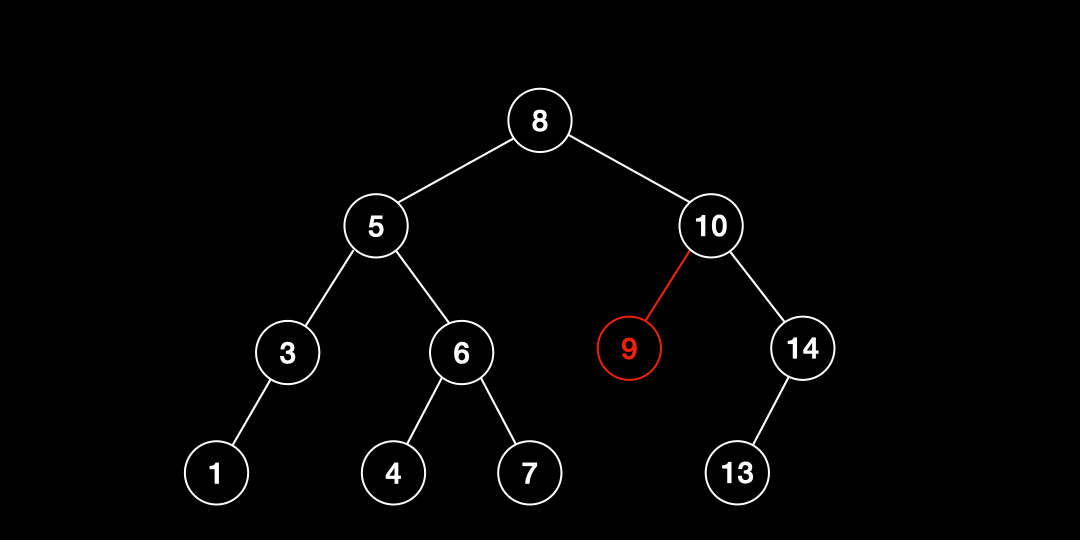
이진탐색트리에서 추가되는 데이터는 항상 리프노드에 삽입된다. 삽입하는 과정은 검색 과정과 거의 유사하다.

1. 삽입하고자 하는 값을 root와 비교한다.
2. 값이 해당 노드의 값보다 작으면 왼쪽 자식노드와, 크면 오른쪽 자식노드와 비교한다.
3. 2번 작업을 리프노드까지 반복한다.
4. 리프노드에 도달한 후 해당 노드의 값보다 작으면 왼쪽에, 크면 오른쪽에 삽입한다.
5. 만약 중복 값을 만나면 그대로 종료한다.

삭제(Deletion)

이진탐색트리에서 특정 노드를 삭제하는 방법은 해당 노드의 자식노드 갯수에 따라 달라진다.

리프노드인 경우

가장 간단한 경우로 삭제하고자 하는 데이터를 검색 후 제거하면 된다.

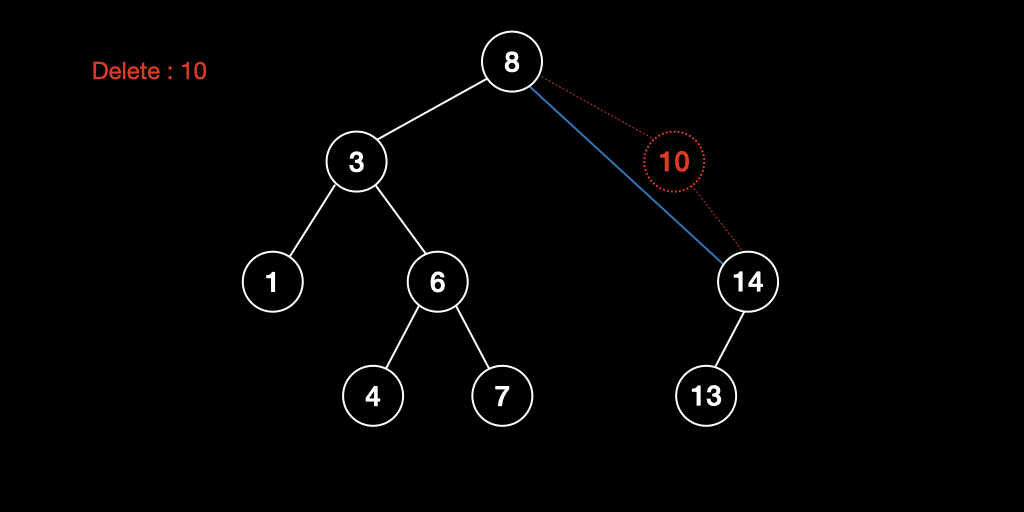
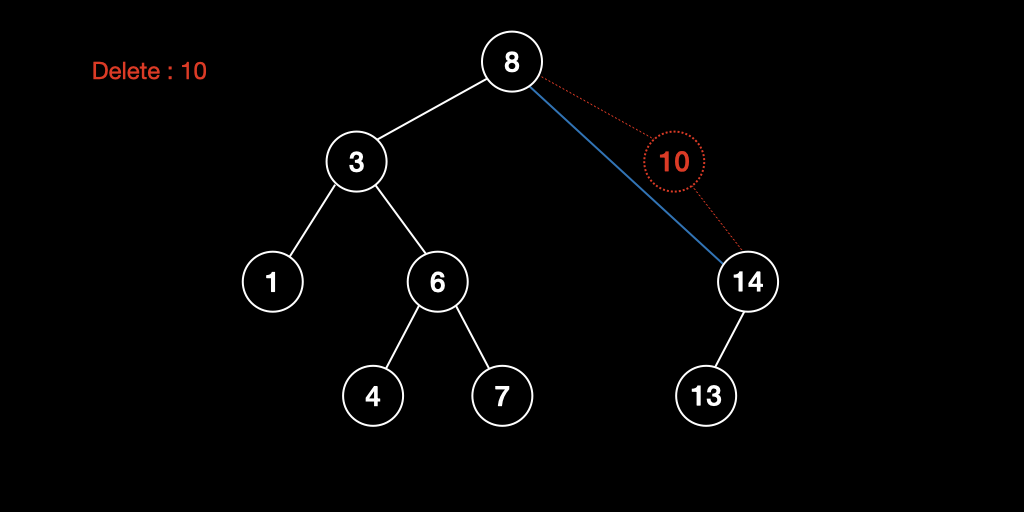
자식노드가 1개 있는 경우

삭제하고자 하는 노드를 제거하고 해당 노드의 자식노드를 부모노드에 직접 연결한다.

자식노드가 2개 있는 경우

자식이 2개 있는 경우는 대체(Replacement) 노드를 찾는 과정이 추가된다. 대체노드를 선정하는 방법은 두 가지가 있다.

• 삭제 대상 노드의 왼쪽 서브트리에서 가장 큰 값을 가지는 노드

• 삭제 대상 노드의 오른쪽 서브트리에서 가장 작은 값을 가지는 노드

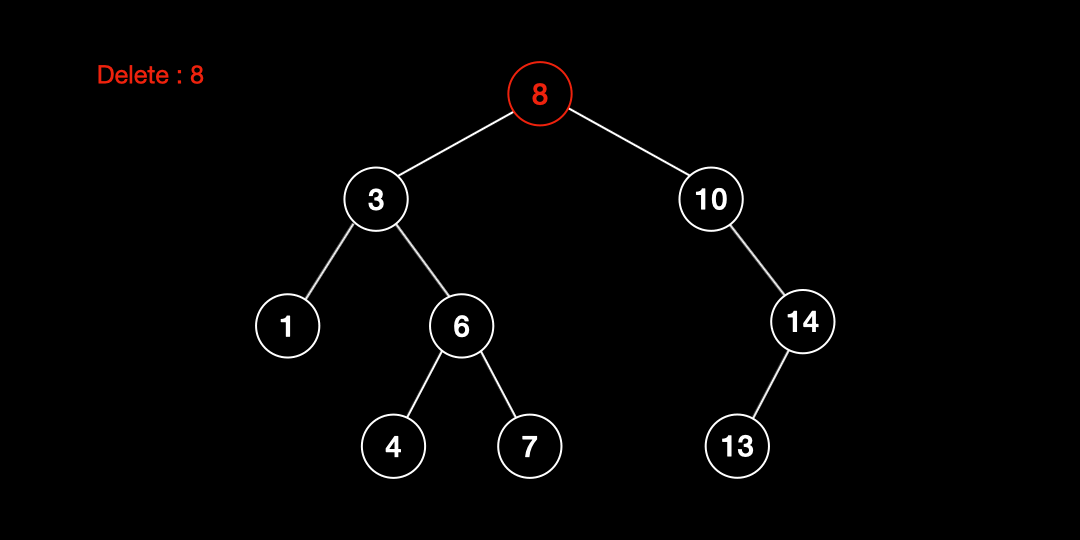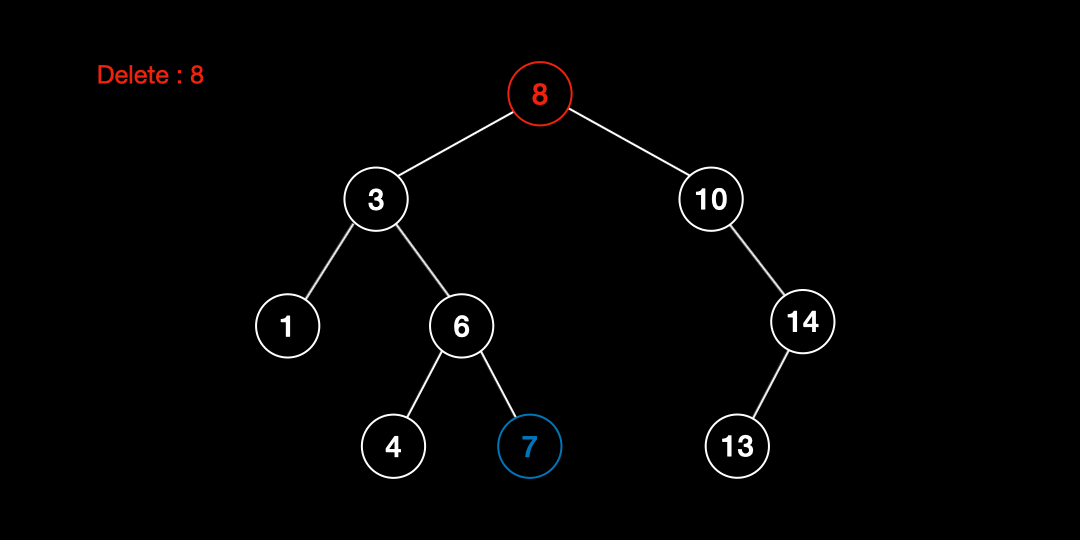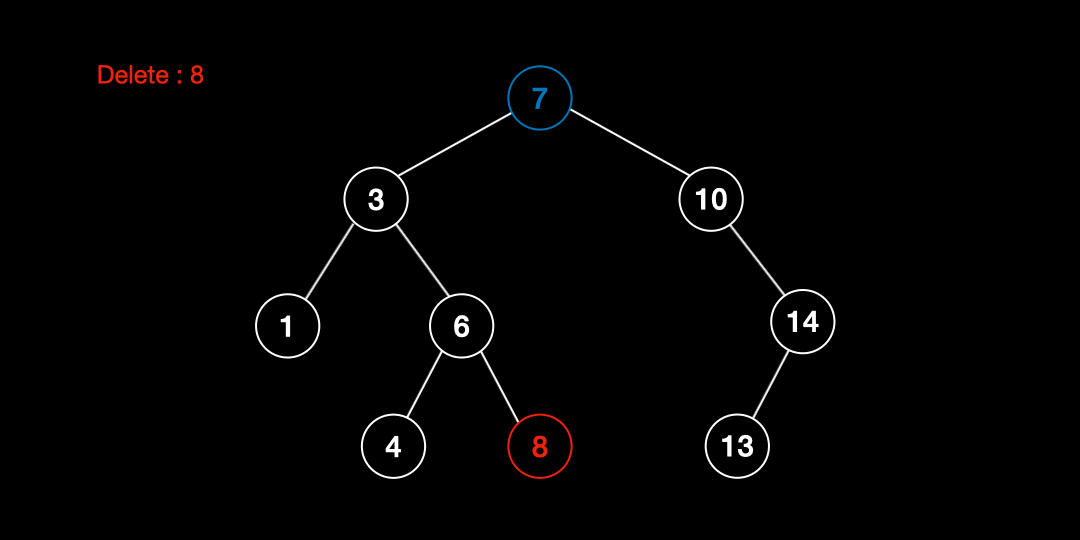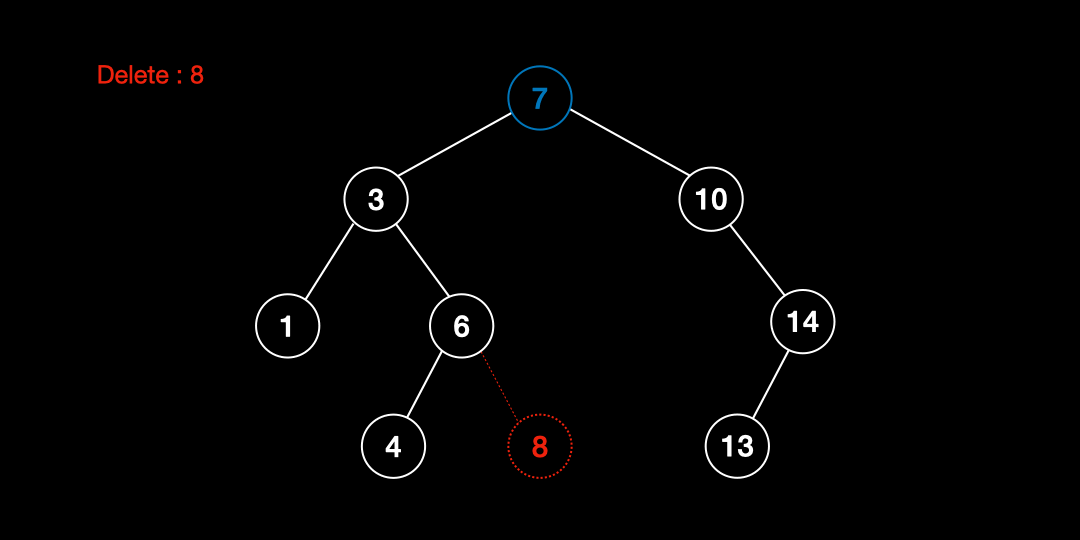
  위 두 가지 방법중 하나를 선택해 대체 노드 찾은 후 삭제하고자 하는 노드와 swap 한 후 삭제를 진행한다.

1. 삭제할 노드를 찾는다.
2. 삭제할 노드의 대체 노드를 찾는다.
3. 삭제할 노드와 대체 노드의 위치를 바꾼다.
4. 노드를 삭제한다.

BST Vs Heap

	BST	Heap
구조	이진트리	완전이진트리
중복값	X	O
삽입/삭제	O(logN)	O(logN)
검색	O(logN)	O(N)

---

Reference

• https://www.geeksforgeeks.org/introduction-to-binary-search-tree-data-structure-and-algorithm-tutorials/