Heap은 어떤 자료구조일까?

앞서 정리한 Queue에서 확장된 자료구조인 Priority Queue는 낮은 시간복잡도를 보장하기 위해 Heap으로 구현한다.

힙(Heap)은 완전이진트리(Complete Binary Tree)의 일종으로 우선순위 큐(Priority Queue)를 구현하는데 사용되는 자료구조이다.

힙에는 최대 힙(Max Heap)과 최소 힙(Min Heap)이 있다. 부모노드의 값이 자식노드보다 크거나 같으면 최대 힙, 부모노드의 값이 자식노드보다 작거나 같으면 최소 힙이라고 한다.
힙의 시간복잡도는 삽입과 삭제만 봤을때 O(1) 이지만, 최대/최소 힙의 조건이 깨져 재배열 하는데 O(logN) 비용이 소모된다. 일반적으로 Linked List로 구현하는 대부분의 트리 구조와 달리 완전이진트리인 힙은 배열로 구현하는게 더 유리하다.

Heap의 특징

완전이진트리(Complete Binary Tree)

힙은 마지막 레벨을 제외한 모든 레벨이 가득 차 있는 완전이진트리 구조이다. 이러한 특징으로 트리 구조이지만 배열을 사용해서 구현할 수 있으며 O(logN) 의 시간복잡도를 보장한다.

최대/최소값 찾기에 최적화

힙은 배열의 최대/최소값이 항상 루트노드에 있도록 보장한다. 따라서 O(1) 비용으로 최대/최소값을 찾을 수 있다.

효율적인 삽입/삭제

힙에 데이터를 삽입/삭제하는데는 O(logN) 비용이 소요된다. 데이터 삽입시에는 배열의 끝에 데이터가 추가되고 부모노드와 크기를 비교하며 교환이 이루어지고, 데이터 삭제시에는 루트노드에 마지막 값이 들어온 후 자식노드와 크기를 비교하며 교환이 이루어진다.

Heap의 종류

최대 힙(Max Heap)

최대 힙은 부모노드의 값이 자식노드의 값보다 크거나 같은 완전이진트리를 말한다.

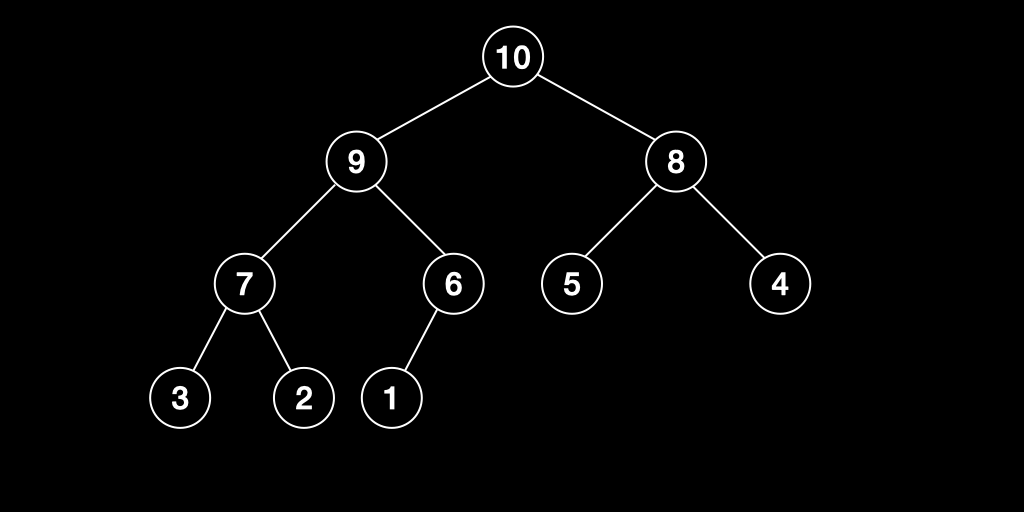
최소 힙(Min Heap)

최소 힙은 부모노드의 값이 자식노드의 값보다 작거나 같은 완전이진트리를 말한다.

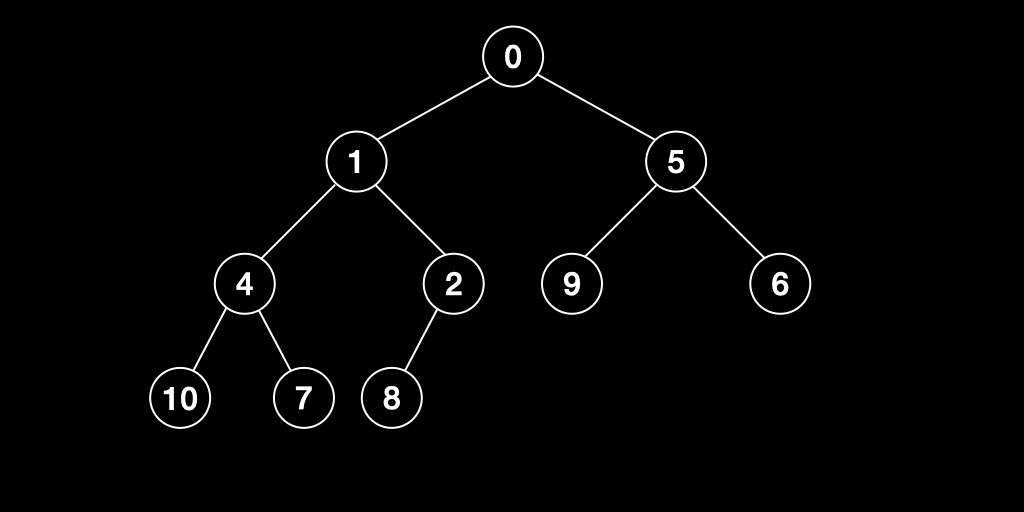
Heap의 연산

Max Heap을 예시로 힙 연산을 설명한다.

삽입(Insertion)

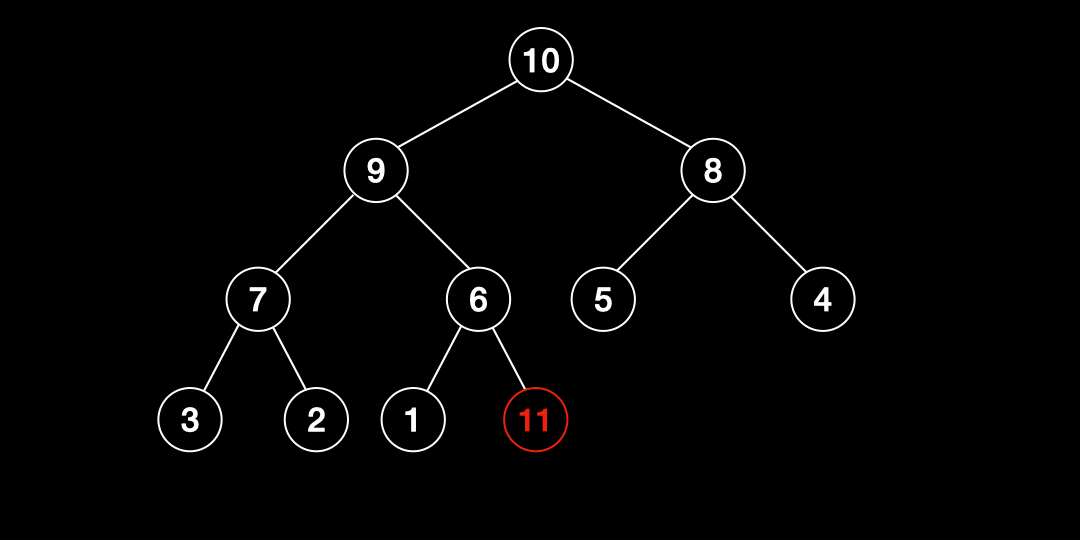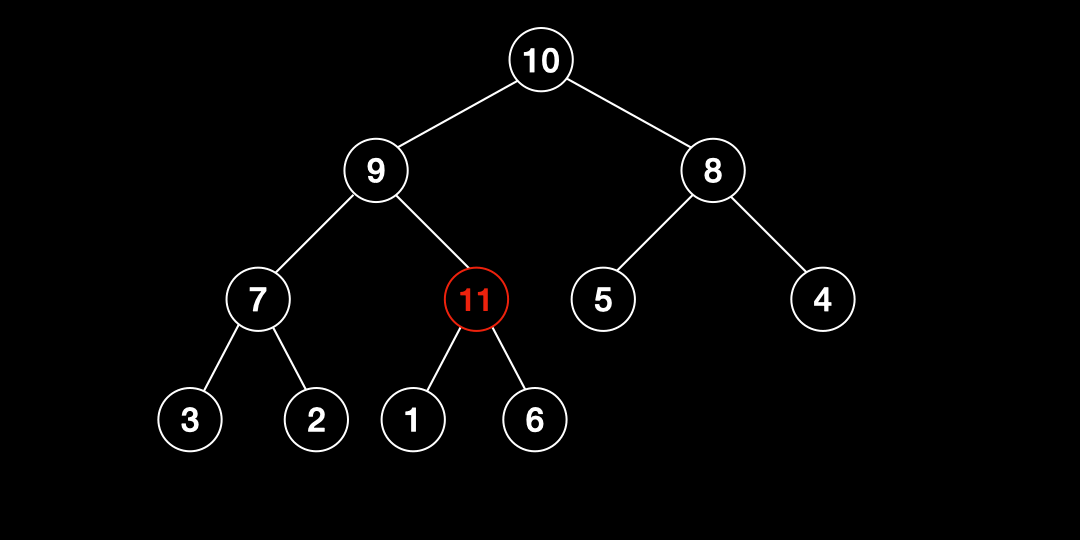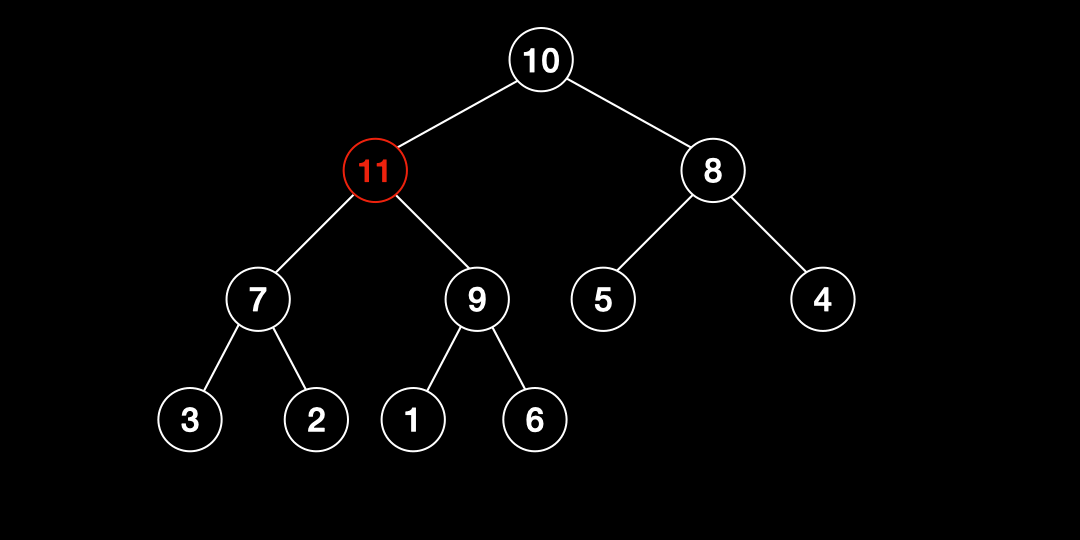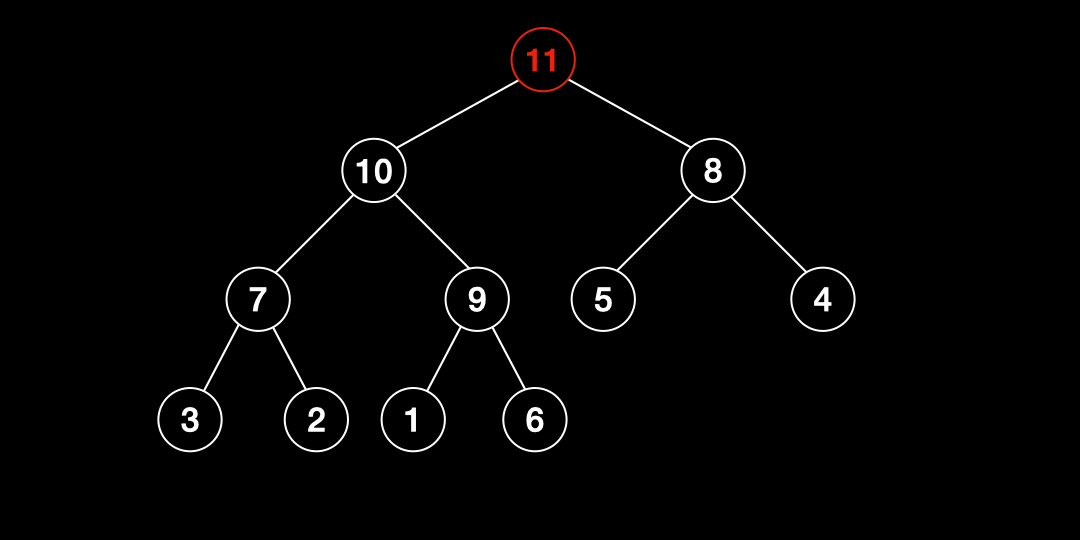
1. 힙의 끝 부분에 데이터를 추가한다.
2. 추가한 값이 부모노드의 값보다 크면 교환하고 그렇지 않으면 중단한다.
3. 2번 작업을 0번 인덱스까지 반복한다.

삭제(Deletion)

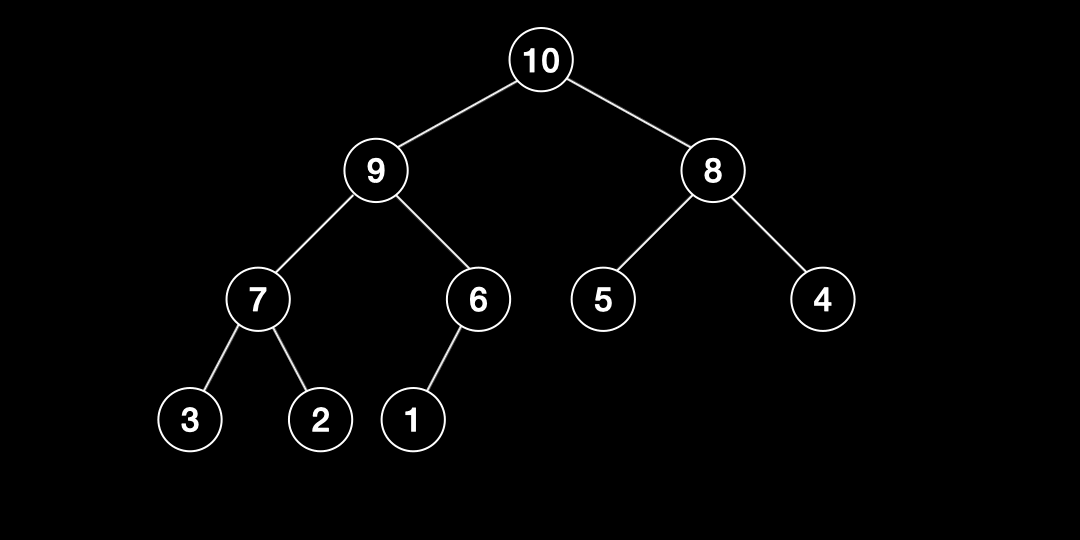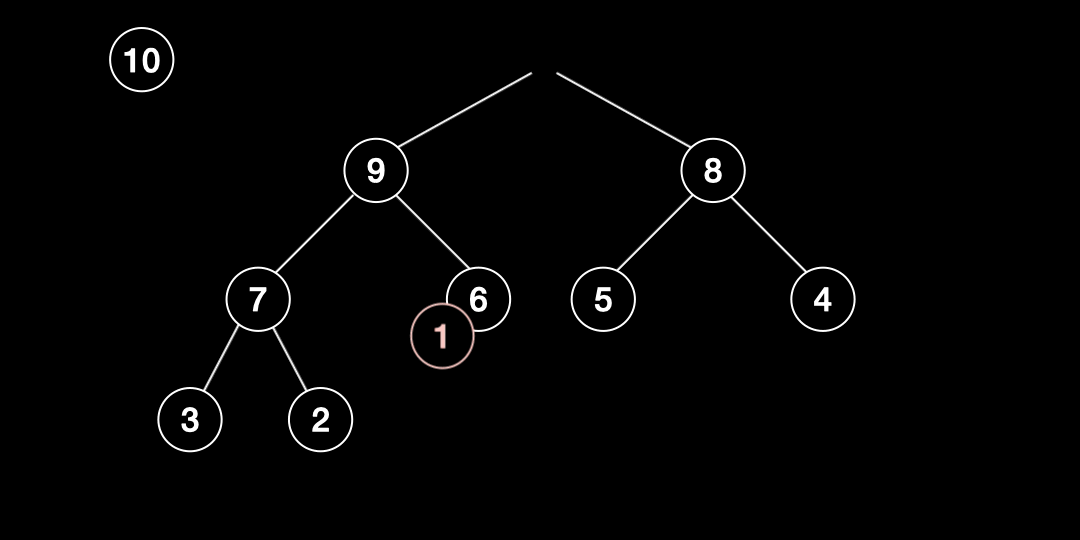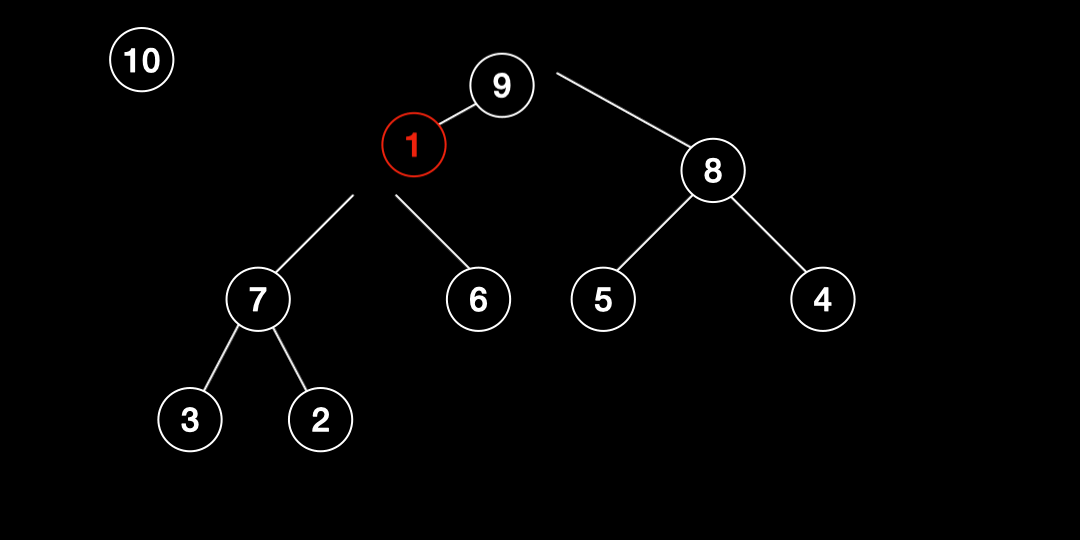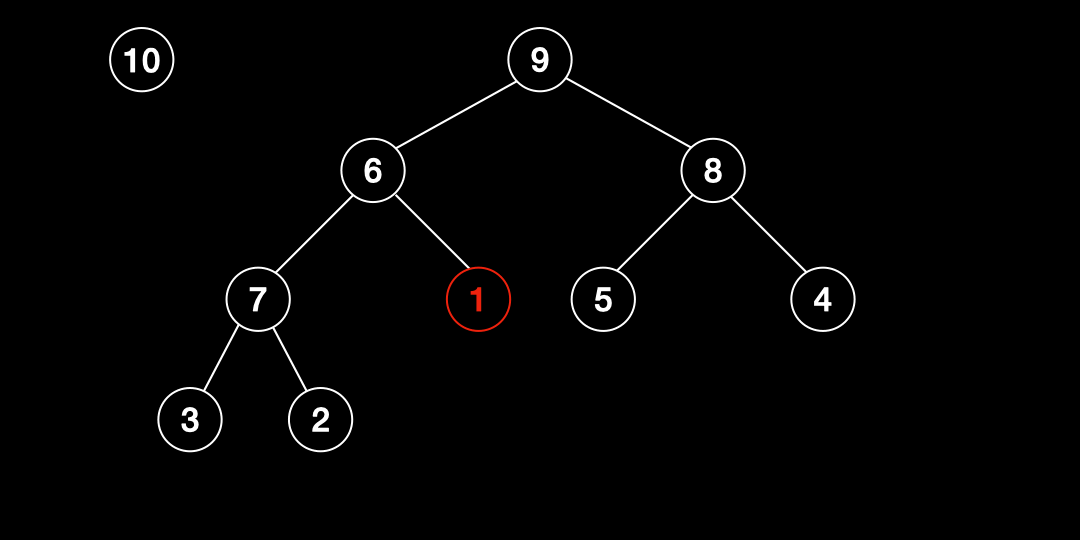
1. 루트노드의 값을 빼고 그 자리에 마지막 인덱스의 값을 넣는다.
2. 자식노드의 보다 큰 경우 교환하고 그렇지 않으면 중단한다.
3. 2번 작업을 마지막레벨까지 반복한다.

재배열(Heapify)

재배열 하는 방법은 다양하다. 위 이미지의 heapify 방식은 마지막 인덱스의 값부터 부모노드와 자식노드를 비교하며 더이상 교환되지 않을때 까지 반복 수행하는 방식이다.

---

Reference

• https://www.geeksforgeeks.org/heap-data-structure/?ref=lbp