Dynamic Array는 Static Array의 고정된 크기의 한계를 개선한 선형 자료구조로서 아래와 같이 정의할 수 있다.
동적 배열(Dynamic Array)은 고정된 크기인 배열의 용량을 유동적을 조절하여 저장하는 자료구조이다.
동적 배열는 정적 배열의 가장 큰 단점인 고정된 크기(size)를 보안하고자 고안된 자료구조로서, 용량(capacity)의 개념을 적용해 한계를 극복했다.
Dynamic Array의 특징
1. Resizing
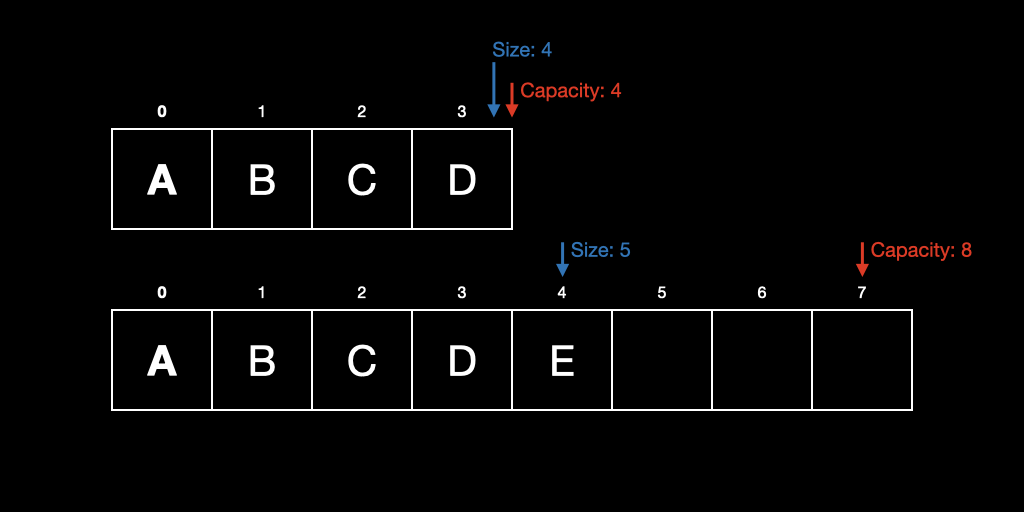
새로운 데이터를 추가함으로서 이미 선언된 배열의 길이를 초과할 때, 기존의 길이보다 더 긴 새로운 배열을 선언하고 그곳에 데이터를 복사하는 과정을 Resize라고 한다. 동적 배열을 사용함으로써 길이를 알지 못하더라도 배열을 선언할 수 있다.
Resizing을 하는 방법은 여러 가지가 있는데, 대표적으로 기존 크기의 2배를 하는 doubling이 있다.
Python의 list resizing을 위한 CPython 코드를 보면 아래와 같다. 참조
/* This over-allocates proportional to the list size, making room
* for additional growth. The over-allocation is mild, but is
* enough to give linear-time amortized behavior over a long
* sequence of appends() in the presence of a poorly-performing
* system realloc().
* Add padding to make the allocated size multiple of 4.
* The growth pattern is: 0, 4, 8, 16, 24, 32, 40, 52, 64, 76, ...
* Note: new_allocated won't overflow because the largest possible value
* is PY_SSIZE_T_MAX * (9 / 8) + 6 which always fits in a size_t.
*/
new_allocated = ((size_t)newsize + (newsize >> 3) + 6) & ~(size_t)3;
/* Do not overallocate if the new size is closer to overallocated size
* than to the old size.
*/위 코드를 보면 2배씩 크기를 키우다가 일정수준 이상 되면 4의 배수로 길이를 늘리는 것을 알 수 있다.
2. Amortized Time Complexity
알고리즘 또는 데이터 구조의 연산 시간 복잡도를 평균적으로 나타내는 개념이다.
일반적으로 최악의 경우를 고려해 시간복잡도를 계산하는 것 과는 조금 다르게, 일부 연산이 높은 비용으로 수행될 수 있지만, 다른 연산이 낮은 비용을 가지며 전반적으로 평균 비용이 낮아지는 것을 의미한다.
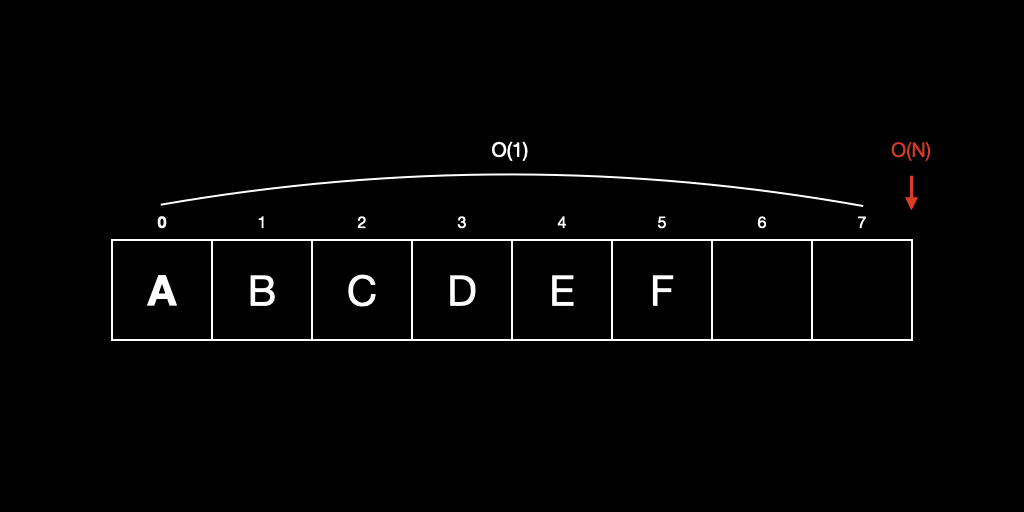
동적 배열에 append 연산시 doubling이 발생하게 되면 O(N) 의 비용이 발생하지만, 그렇지 않은 경우에는 O(1) 의 비용으로 연산이 가능하다.
이러한 케이스를 분할상환 시간복잡도(Amortized Time Complexity) 라고 하며 동적 배열의 append 연산은 Amortized O(1) 이라고 할 수 있다.
Dynamic Array의 시간복잡도
1. 조회(lookup)
메모리상에서 연속적인 데이터를 임의 접근(Random Access)하기 때문에 O(1) 의 시간이 소요된다.
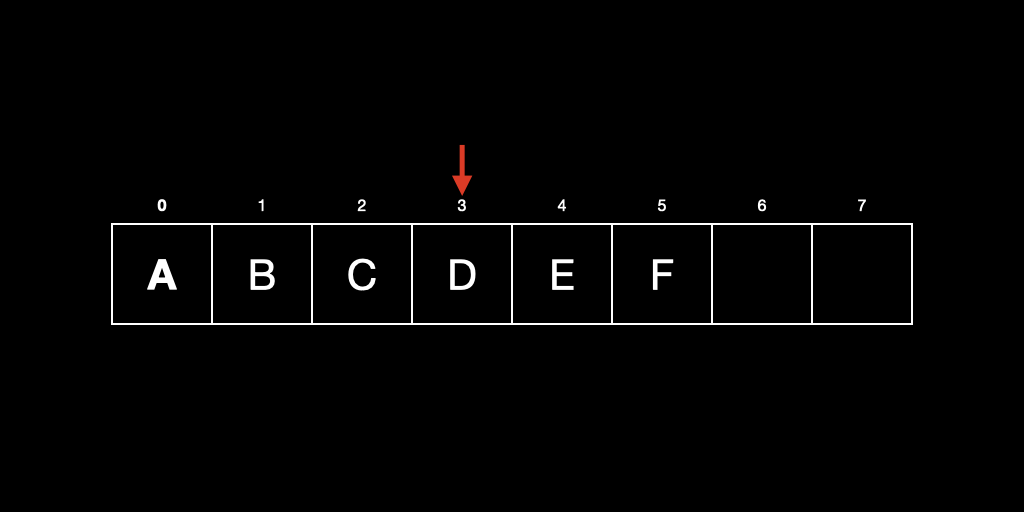
2. 추가(append)
미리 할당된 용량을 초과하는 경우 O(N) 이며, 할당된 용량 이내의 범위에서는 O(1) 이다. 즉, Amortized O(1) 이다.
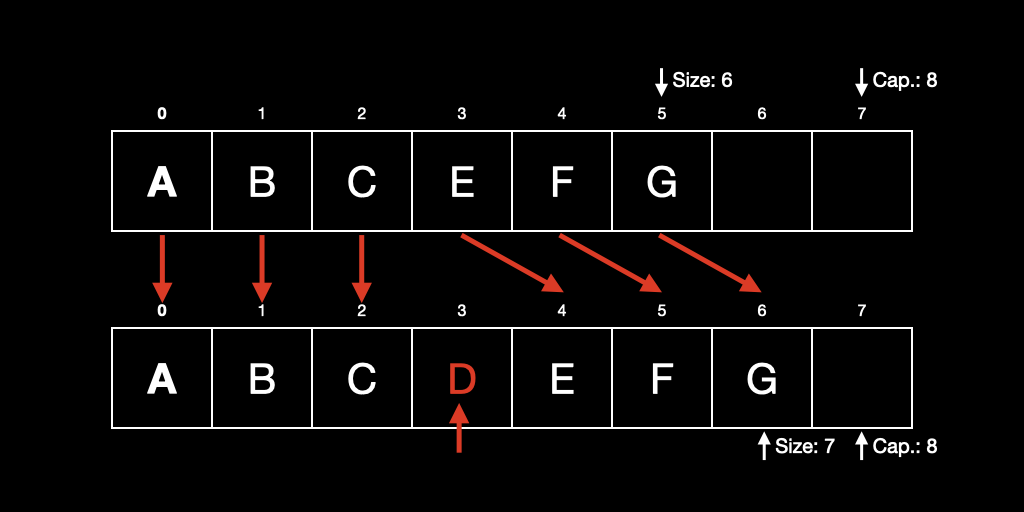
3. 삽입(insertion)
삽입하고자 하는 인덱스 이후의 데이터를 모두 뒤로 옮겨야 하므로 O(N) 이다.
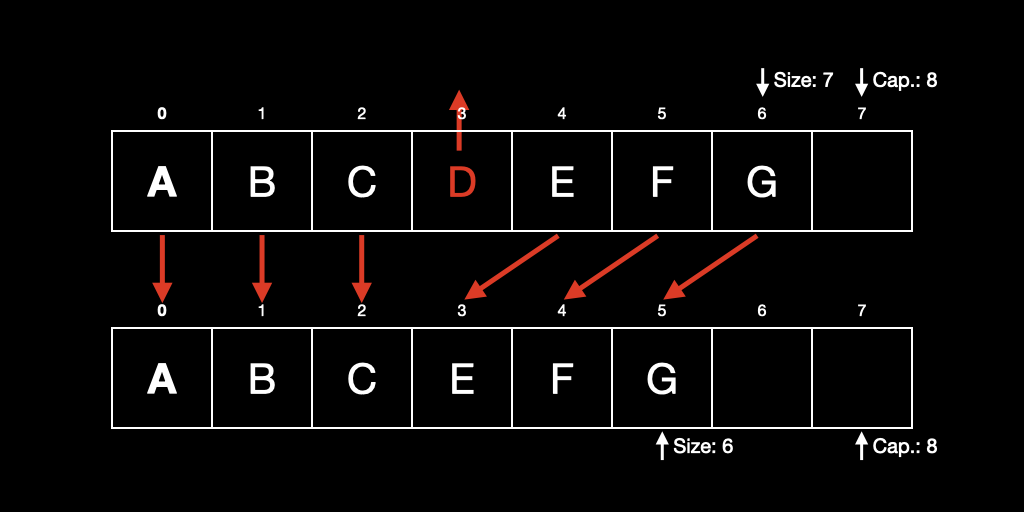
4. 삭제(deletion)
삭제하고자 하는 인덱스 이후의 데이터를 모두 앞으로 옮겨야 하므로 O(N) 이다.
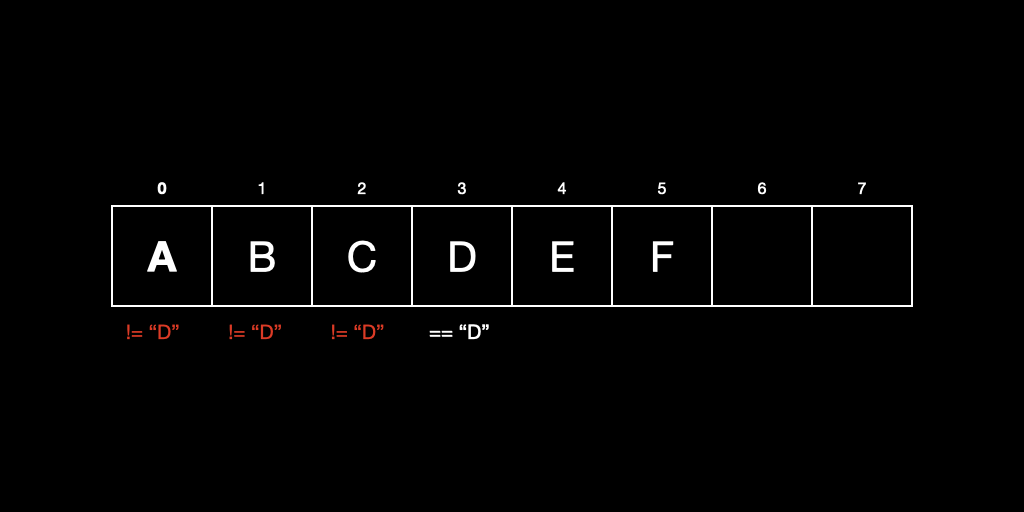
5. 검색(search)
첫번째 인덱스부터 값을 비교하며 찾아야 하므로 시간복잡도는 O(N)이다.
요약
| Operation | Average Case |
|---|---|
| 조회(lookup) | O(1) |
| 추가(append) | Amortized O(1) |
| 삽입(insertion) | O(N) |
| 삭제(deletion) | O(N) |
| 검색(search) | O(N) |
장점
- 빠른 조회: 길이에 상관 없이 O(1) 로 접근이 가능하다.
- 유동적인 크기: 원하는 갯수만큼 O(1) 로 데이터 추가가 가능하다.
- 빠른 데이터 추가: Array의 비어있는 공간에 O(1) 로 추가가 가능하다.
단점
- 높은 Resizing 비용: 평균적인 append 연산은 O(1) 로 수행하지만, 크기 초과시 O(N) 의 비용이 든다.
- 삽입, 삭제시 낮은 성능: 해당 연산시 새로운 배열을 생성후 메모리 복제로 인해 O(N)으로 동작한다.

