Linked List를 간단히 정의하면 아래와 같다.
Linked List는 노드(Node)라는 구조체로 이루어져있는데, 물리적인 메모리상에서는 비연속적으로 저장이 되지만 각각의 노드가 다음 노드의 주소를 가리킴으로써 논리적인 연속성을 가진 자료구조이다.
Linked List는 처음과 끝 위치에 한해서 O(1) 비용으로 데이터를 추가/삭제가 가능하다. Dynamic Array를 resize 할 경우 발생하는 doubling 이슈를 해결한 자료구조 라고 할 수 있다. 하지만, 분산되어있는 데이터로 인해 cache-friendly 하지 않으며 임의 접근(random access)이 아닌 순차 접근(sequential access) 으로 데이터 조회가 느리다는 단점이 있다.
대표적으로 노드에 Value와 다음 노드의 주소만을 저장하는 Singly Linked List가 있으며, 추가적으로 이전 노드의 주소를 저장하는 Doubly Linked List, Head 노드와 Tail 노드를 연결한 Circularly Linked List 등 노드를 어떻게 구성하는지에 따라 다양한 형태의 Linked List를 만들 수 있다.
Linked List의 특징
Node
배열에 인덱스가 있다면 Linked List에는 노드가 있다. 실제 메모리상에 데이터를 순차적으로 저장하는 배열은 인덱스를 사용한 임의 접근(random access)으로 데이터 조회시 O(1)이 소요된다. 하지만 Linked List는 실제 메모리상에 분산 저장되어있는 노드들이 논리적으로 연결되어 있어 순차 접근(sequential access)하므로 데이터 조회 속도가 O(N)이 소요된다.
데이터 조회 속도는 느리지만 가장 처음 또는 가장 뒤의 데이터를 추가/삭제 하는데는 O(1) 비용으로도 가능하다. 배열과 달리 고정된 크기가 아니기 때문에 모든 메모리 공간이 가득찾지 않은 한 O(1) 비용으로 추가가 가능하다.
cache-frieldly 하지 않음
CPU가 연산을 하기 위한 데이터를 읽어올 때 메인 메모리 보다 cache 메모리에서 가져오는게 더 빠르게 동작한다. 따라서 개발할 때 cache를 고려한 설계를 하는게 큰 장점이 될 수 있는데, 이를 가능하게 하는 몇가지 요인이 있다.
- 공간적 로컬리티(Spatial locality): 실제 메모리에서 서로 가까운 위치에 있는 데이터가 함께 사용될 확률이 높은 특성을 말한다.
- 시간적 로컬리티(Temporal locality): 단기간에 반복적으로 사용되는 데이터가 가까운 미래에 다시 사용될 가능성이 높은 속성을 말한다.
- 데이터 크기(Data size): Cache가 대용량 데이터 구조를 저장하지 못할 수 있으며, 이로 인해 cache가 누락되고 성능이 저하된다.
- Cache 크기(Cache Size): 크기가 작은 cache는 프로그램이 액세스해야 하는 모든 데이터를 저장할 수 없는 반면 크기가 큰 cache는 자주 액세스하지 않는 데이터를 저장할 확률이 높아 cache 미스가 더 많을 수 있다.
실제로 Python에서 배열와 Linked List의 cache 효과를 비교해보면 아래와 같다.
import time
# 1천만 개의 정수를 담은 배열을 생성
arr = [i for i in range(10_000_000)]
# 1천만 개의 노드를 가진 Linked List 생성
class Node:
def __init__(self, value=0, next=None):
self.value = value
self.next = next
head = Node(0)
prev = head
for i in range(1, 10_000_000):
node = Node(i)
prev.next = node
prev = node
# 배열에서 모든 값을 더하는 시간을 측정
start_time = time.time()
arr_sum = sum(arr)
end_time = time.time()
duration = end_time - start_time
print(f"Sum of array: {arr_sum:,}. Time taken: {duration:.5f} seconds.")
# Linked List에서 모든 값을 더하는 시간을 측정
start_time = time.time()
curr = head
ll_sum = 0
while curr is not None:
ll_sum += curr.value
curr = curr.next
end_time = time.time()
duration = end_time - start_time
print(f"Sum of linked list: {ll_sum:,}. Time taken: {duration:.5f} seconds.")Sum of array: 49,999,995,000,000. Time taken: 0.04843 seconds.
Sum of linked list: 49,999,995,000,000. Time taken: 1.14649 seconds.정확한 실험이 아닐 수 있지만 동일한 작업에 대해 Array가 20배 가량 더 빠른 성능을 보였다.
Linked List의 시간복잡도
1. 조회(lookup), 검색(search)
메모리상에서 불연속적으로 데이터를 순차 접근만 가능하기 때문에 O(N) 의 시간이 걸린다.
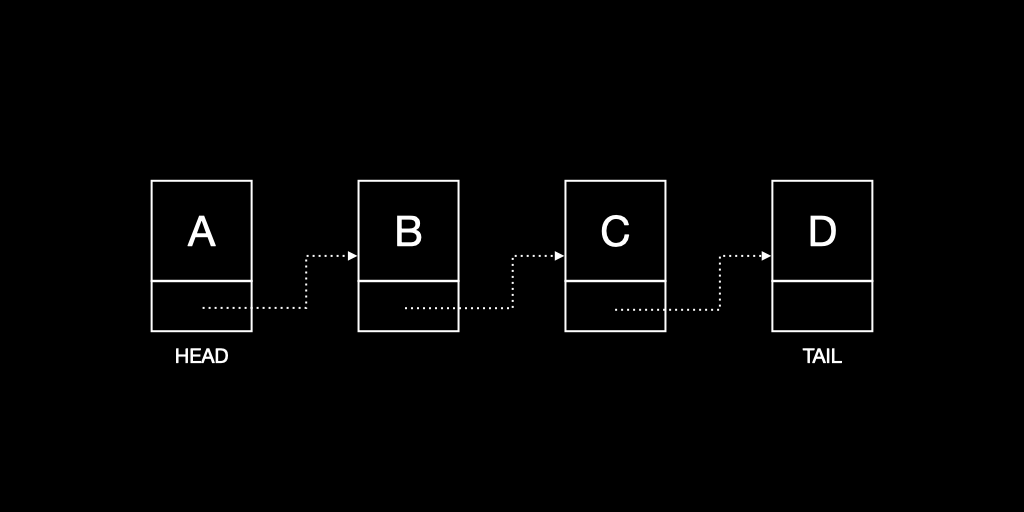
2. 추가(append)
첫 번째 요소로 추가 또는 마지막 요소로 추가인지에 따라 다르다. 첫 번째 요소로 추가된다면 O(1) 의 시간이 소요되고, 마지막 요소로 추가된다면 순환 시간이 포함된 O(N) 의 시간이 소요된다.
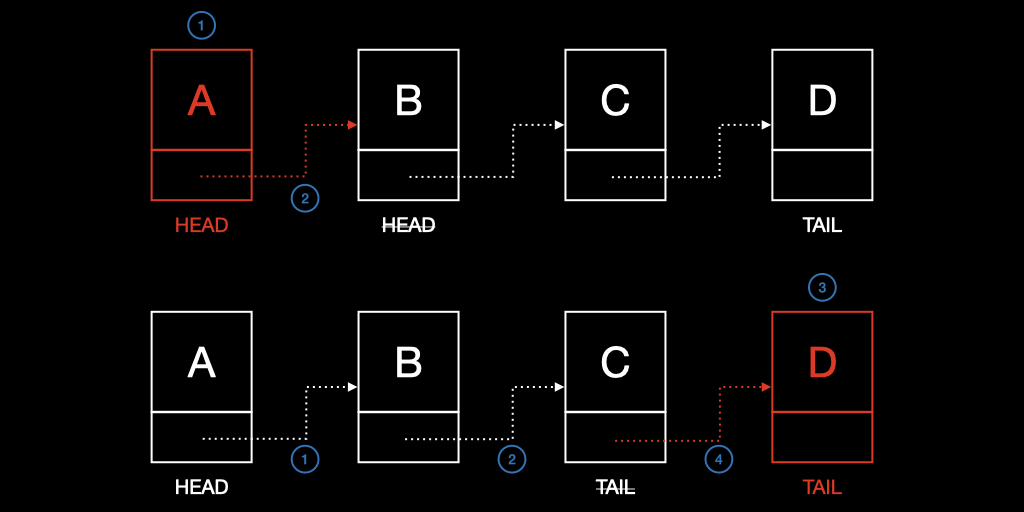
4. 삽입(insertion)
추가 데이터 삽입시 다음 Node를 가르키는 주소만 변경하면 되므로 O(1) 의 시간이 소요되지만, 해당 노드를 검색하는 시간이 추가되므로 실질적으로 O(N) 의 시간이 소요된다.
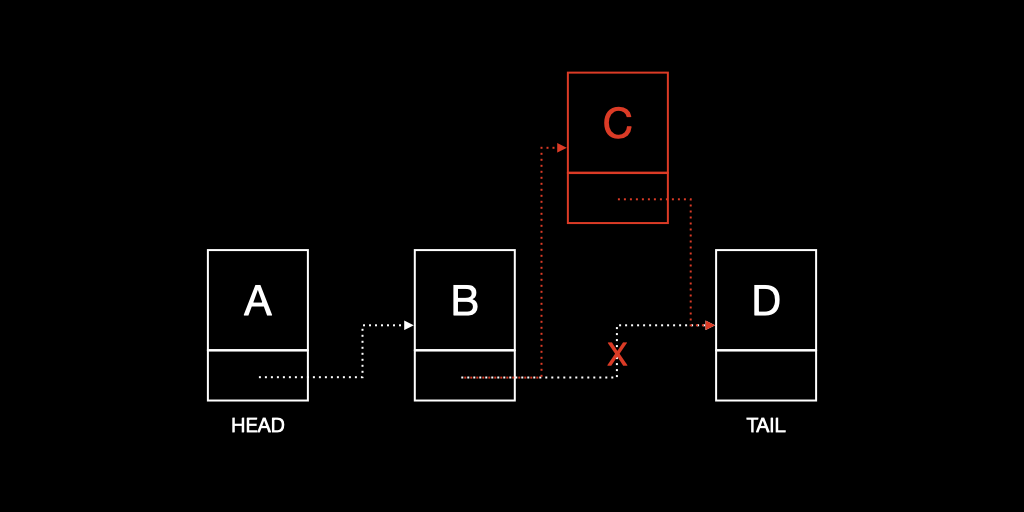
5. 삭제(deletion)
삽입과 마찬가지로 데이터 삭제시 다음 Node를 가르키는 주소만 변경하면 되므로 O(1) 의 시간이 소요되지만, 해당 노드를 검색하는 시간이 추가되므로 실질적으로 O(N) 의 시간이 소요된다.
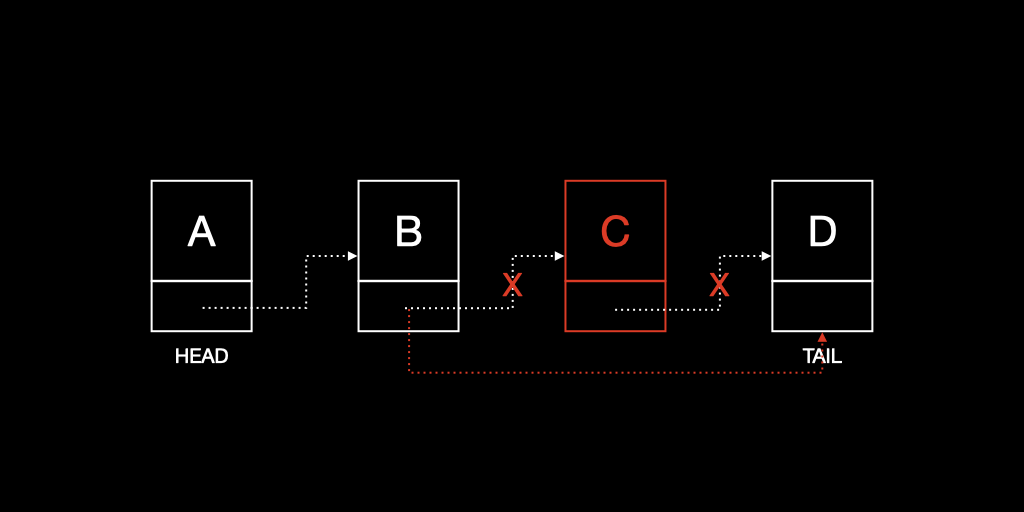
요약
| Operation | Average Case |
|---|---|
| 조회(lookup), 검색(search) | O(N) |
| 추가(append) | O(1) | O(N) |
| 삽입(insertion) | O(N) + O(1) |
| 삭제(deletion) | O(N) + O(1) |
장점
- 양 끝에서 빠른 데이터 추가: 길이에 상관 없이 O(1) 로 작업이 가능하다.
- 유동적인 크기: 메모리에 공간이 남아있는 한 데이터 추가가 가능하다.
단점
- 높은 조회/검색 비용: 시작 또는 끝 지점만 알고있기 때문에 순환 비용으로 O(N) 이 소요된다.

