행렬미분 스터디 6주차 정리

수학적 최적화란 무엇인가?

Optimization이란?

어떤 함수를 최소화/최대화/하는 argument x를 탐색하자!
$min f(x)$
$max f(x)$
$arg: min f(x)$

이것이 왜 중요한가? 모든 수학을 통틀어서 결국은 어떤 조건을 만족하는 집합을 구하는 일, 즉 집합론이 가장 중요한 것인데 어떤 input이 들어갔을 때 이전의 단계인 기대되는 f(x)값을 모르는 단계에서 (야코비안) 미분값을 알 수 있게 되는 f(x)를 만드는 단계로 넘어간 것이다.

그렇다면, 왜 어려웠던 것인가?

f(x) 식 자체를 알 수 없는 경우가 많기 때문이다.
그렇다면 식을 몰라도 값을 계산할 수 있는 경우가 있다는 것인데, 이것이 현재의 머신러닝과 딥러닝이 처한 현실이다. 당장 손실함수만 보아도 함수값을 정확히 계산할 수 없게 된다. 하지만, f(x)가 '미분 가능하다'는 조건을 가지고 있다면 1차 근사는 가능하다.
예를 들어, 손실함수에서는 loss 값, cost 값은 미분 연산(역전파 등)을 활용해서 1차 미분값을 알아내는 정도에 그치는 것이다.

$f(x)$
$f(a) + <\nabla f(a)(x-a)> + \cdot (||x-a||^2)$

$f(a) + <\nabla f(a)(x-a)>$ 쯤을 파악하는 것이다.

$min_x f(x)$ => $min_x {<\nabla f(a)^T, (x-a)>}$
문제는 $min_x {<\nabla f(a)^T(x-a)>}$ 이 부분이 x=a(a는 상수)에서의 저평면(hyperplane)이라서 최소값을 찾으면 마이너스 무한대 값이 나오게 되는 것이다. 선형성을 갖는 함수라서 그러하다.

1. 최소값을 찾아내고 싶었던 f(x)를 찾아낼 수 없다.
2. x=a 에서 멀어질수록 1차 근사값의 오차가 커진다.

해결책으로, 아래와 같은 식이 제안됐다.

$f(a) - {\nabla f(a)^T(x-a)} + \eta (||x-a||^2_2)$

이때 eta는 양의 실수, norm 은 x와 a 사이의 거리를 매 iteration마다 함수를 최소화해주는 패널티항이다. 이 패널티항이 gradient descent 인 것이다.

Gradient Descent

미분, 편미분 방정식을 iteration 을 활용하여 반복적으로 사용할 수 없을까? 라는 아이디어로 생긴 Gradient Descent는 앞서 설명한 패널티항의 개념을 이해하는 것이 중요하다.

x와 a 사이의 거리의 제곱이라는 패널티를 가해주는 항의 세기를 에타로 작게 조정한다는 의미는, step size가 작을 때 조금만 이동하며 x가 a에서 멀리 떨어지는 것을 허용하는 것이다. 에타를 크게 조정하는 것은 x가 a에서 멀리 떨어질수록 패널티를 강하게 준다는 것을 의미한다.

이것이 Gradient Descent이다.

힐베르트 공간과 바나흐 공간에서 Gradient와 미분은 '내적:Gradient의 변화와 관련'과 'Norm:알고리즘의 변화와 관련'을 유도하기 때문에 중요하다. 따라서 내적과 Norm(자기 자신과의 내적)을 이야기한 후에 Gradient를 논할 수 있게 된다.

2차 테일러 근사

f의 x=a에서의 헤시안 : 함수의 곡률 정보를 담고 있는, 2번 미분 시 나오는 값

원래는 Identity 함수가 2차 헤시안 커버쳐 정보가 되어야 하는데, gradient descent의 1차 미분정보를 쓰는 함수들은 결국 무시(커버)하는 것이다.

$min_x {f(x)+\nabla f(a)^T(x-a)+1/2(x-a)^T I (x-a)}$
$min_x {f(x)+\nabla f(a)^T(x-a)+1/2(x-a)^T H(a) (x-a)}$

$x=a- H(a) \nabla f(a)$

언제 iteration을 끝내는가?

$min_x f(x) : x_t = x_{t-1} - \eta \nabla f(x_{t-1})$ ($\nabla >0, ∀_t \isin N$)
더이상 $x_t$ (Stationary point:극소, 극대를 포함하는 용어)가 바뀌지 않으면 끝이다. Gradient가 0일 때(Gradient Norm이 0일 때) 파라미터가 이동하지 않는 것이므로 업데이트가 끝나는 것이다.

$|| \nabla f(x_t)||= 0$ $<=>$ $x_t = x_{t-1}$

Convex Function

중요성

convex function에서는 local minima가 global minima이기 때문에 극소점이 안장점(saddle point)가 아니면 최소점이 된다. 아주 막강한 특성을 가지고 있는 셈이다.

그렇기 때문에 gradient descent에서 step size가 적절할 때 convex function에서 global minima 로 수렴한다는 것이 논문으로 증명이 된 바가 있어 사용하는 것이다.

따라서 convex function에서는 수학적 최적화를 이끌어낼 수 있다.

특징

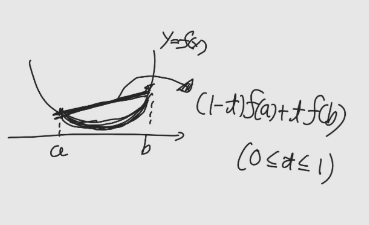
Convex function(볼록함수)의 첫번째 정의에서 임의의 a와 b를 지나는 선분을 그려보면, 항상 선분의 함수값이 함수값보다 크다는 사실을 알 수 있다.

$f((1-t)a+tb)<=(1-t)f(a)+tf(b)$

두번째 convex의 정의에서는 임의의 a에서 접선의 기울기가 f(x)보다 작거나 같다는 것을 보장함을 알 수 있다.

$f(a)+f'(a)(x-a) <= f(x)$ ,$(∀_a \isin |R)$

세 번째 convex 의 정의는 두 번 미분한 값이 항상 0보다 크거나 같다는 것이다.

$f''(a)>=0$,$(∀_a \isin |R)$