스탠포드 자연어처리 강의를 듣고 블로그로 정리해보기로 한다.
일단 수업과 별개로 놀랐던 점.
- 첫수업부터 엄청난 수학 실력을 뽐내주신다.
- 학생들의 질문이 꽤나 흥미롭다.
- 교수님의 답변도 짱 대박 친절하시다.
아무튼 강의 공부 복습 Let's go
Lecture 1
1일차 강의는 기존 자연어 처리의 문제점과 그걸 해결하는 Word2Vec 기초를 다뤘다.
간략하게 요약할 내용은 다음과 같다.
- Word2Vec introduction
- Word2Vec 목적함수 gradients
- 최적화 기초
전통적인 nlp에서는 우리는 단어를 discrete symbols 로 나타내었다.
one-hot vectors로 나타낼 수 있다.
예를 들면
motel = [0000010000]
hotel = [0001000000]
이렇게 나타내는 것이다.
하지만 이런 discrete symbols에는 문제가 있는데, 벡터 상에서 motel과 hotel의 벡터는 서로 다른 벡터이고 이를 내적하면 0이기 때문에 서로 직교하는 벡터로 자연적으로 관계성이 전혀 없음을 의미한다.
즉 단어의 관계 및 유사성을 찾을 수 없다는 의미이다.
그럼 단어의 관계를 어떻게 찾을까?
Distributional semantics 는 단어의 의미는 그들과 빈번하게 가까이 있는 것으로 부터 주어진다고 말한다. 즉 A라는 단어가 텍스트에서 주어지면 이것의 맥락(context)는 근처에서 보이는 set of words로부터 찾을 수 있다는 것이다. 그리고 단어 벡터를 사용하면 벡터 자체에서 맥락을 찾는 능력을 쉽게 인코딩할 수 있다.
Word Vectors
그래서 하나의 단어에 dense vector를 만든다.
banking = ( 0.243, 0.792, -0.177 ...)
그리고 이러한 벡터는 비슷한 의미를 가진 것끼리 묶인다. (끼리끼리 모인다.)
Word2vec
개요
word2vec는 단어 벡터를 학습하기 위한 프레임워크로 2013년 Mikolov에 의해 개발되었다.
- 일반적으로 크지만 잘려지는 고정된 어휘를 선택하여 희귀한 어휘를 제거한 큰 corpus를 가진다.
- 모든 단어에 대해 벡터를 만들었다.
- 중심 단어 c와 문맥 단어 o가 있는 텍스트의 각 위치 t 를 거친다.
- c 와 o의 단어 벡터의 유사성을 사용하여 c또는 o의 확률을 계산한다.
- 단어에 할당된 확률을 최대화하기 위해 계속 단어 벡터를 조정한다.
즉 확률을 계산하는 것인데
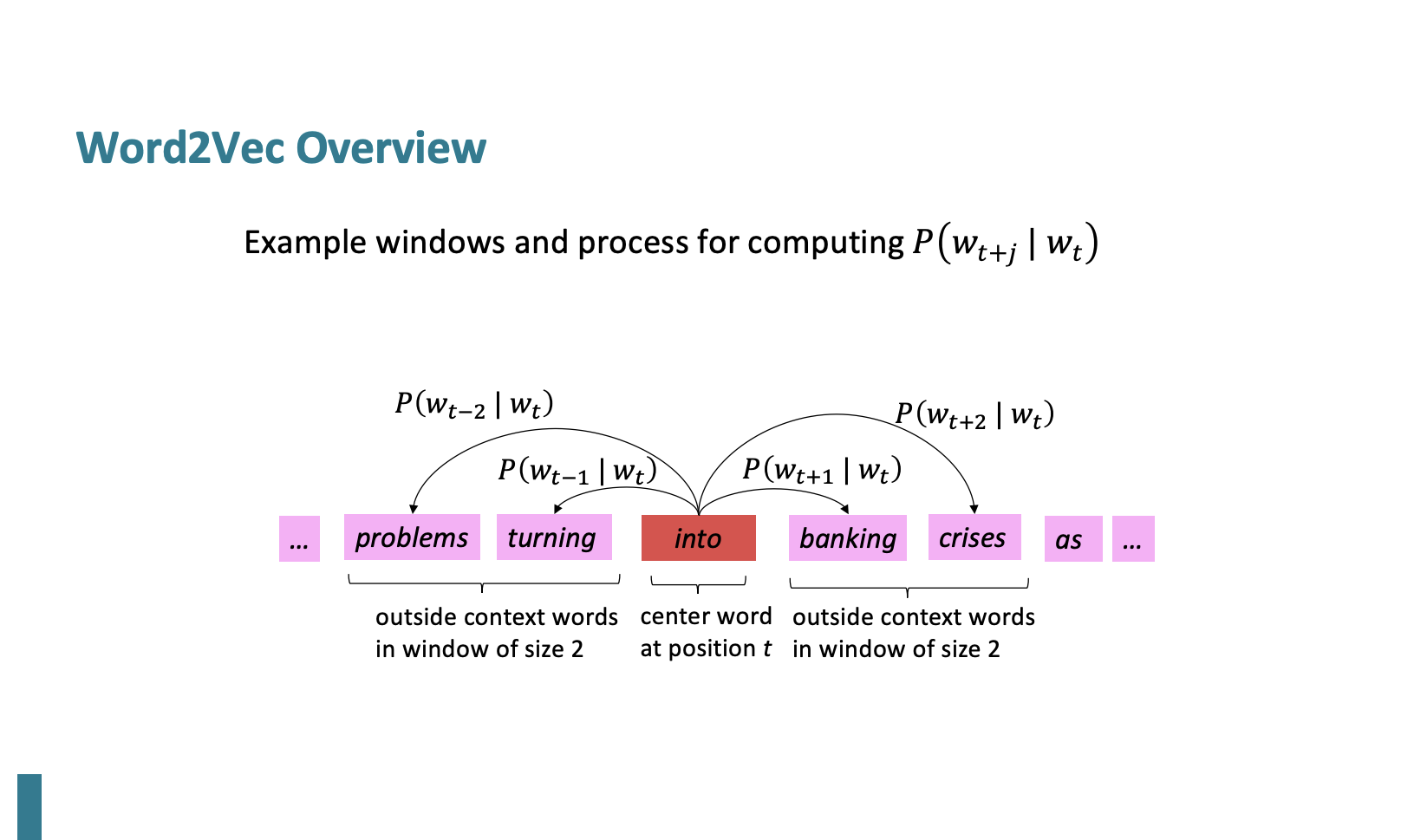
만약 window = 2 이면 앞뒤 -+2단어를 확인하여
into가 나왔을 때 banking이 나올 확률, into 가 나왔을 때 crises가 나올 확률 ,,, 이렇게 확률을 계산하는 것이다.
이 과정을 banking, crises ... 이렇게 이어 나가 계산한다.
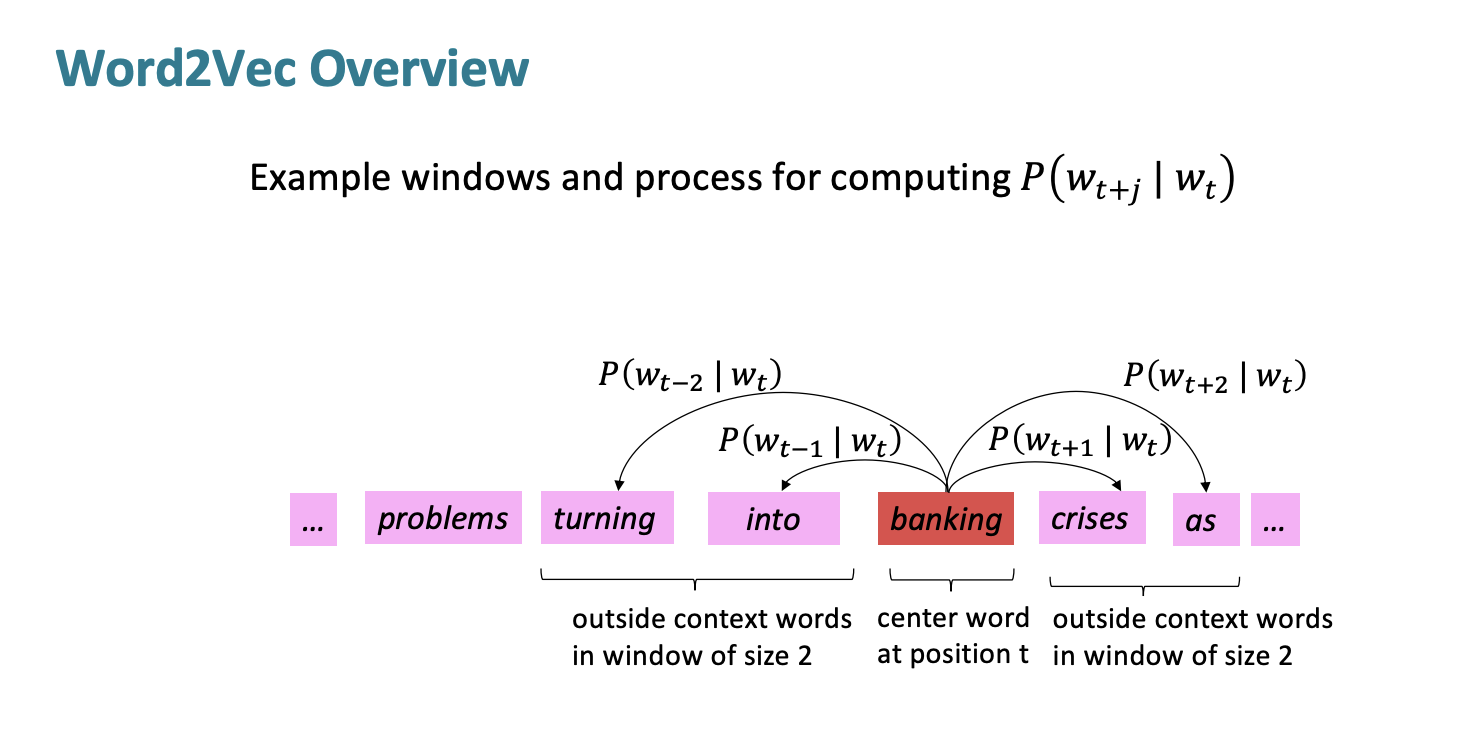
objective function
Likelihood는 주어진 데이터 샘플이 주어진 모델 또는 가설에 얼마나 "적합"한지 나타내는 측도이다.여기서는 그냥 모든 확률을 곱해버린다.

목적함수는 비용함수 또는 손실함수라고 하는데 우리는 목적함수를 최소화 해야한다. 이는 예측 정확성을 최대화하는 것과 같다. 목적함수 앞에 음수를 붙이는 것을 확인하자.
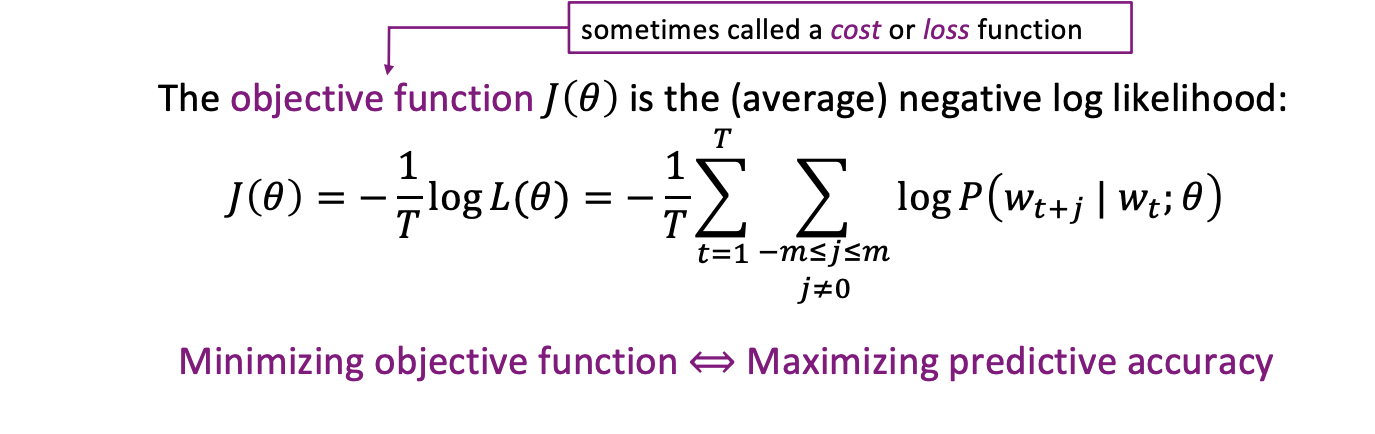
여기서 목적함수란? 최적화 문제에서 문제를 정의하고 해결하는데 중요한 역할을 하는 수학적인 함수이다. 주어진 목표를 최소화 또는 최대화하려는 변수나 매개 변수를 포함하고 있다.
아니 그러면 어쩌다 저 비용함수가 나왔을 까? log 를 붙이면 합계로 변하는 속성을 가지고 있다. 우리는 (average)negative log likelihood를 목적함수로 사용하는 것이다.
그러면 확률(P)은 어떻게 계산할 것인가?
하나의 단어에는 두개의 벡터가 사용된다. 하나는 중심 단어, 나머지는 문맥 단어이다.
u를 문맥단어의 벡터, v를 중심단어의 벡터라고 하자.
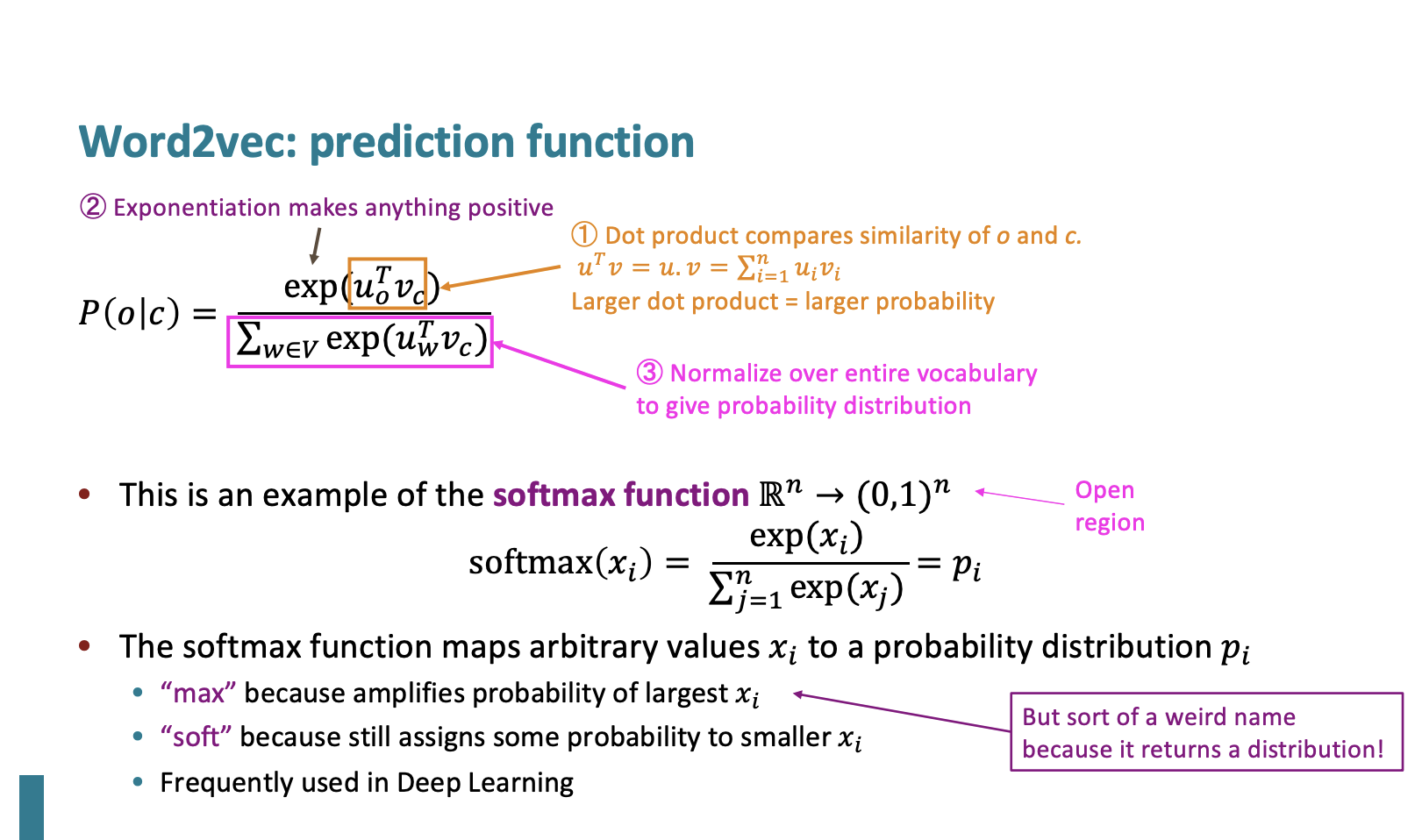
Prediction function
그리고 중심 단어가 나왔을 때의 문맥 단어가 나올 확률을 계산하는 것은 다음과 같이한다.
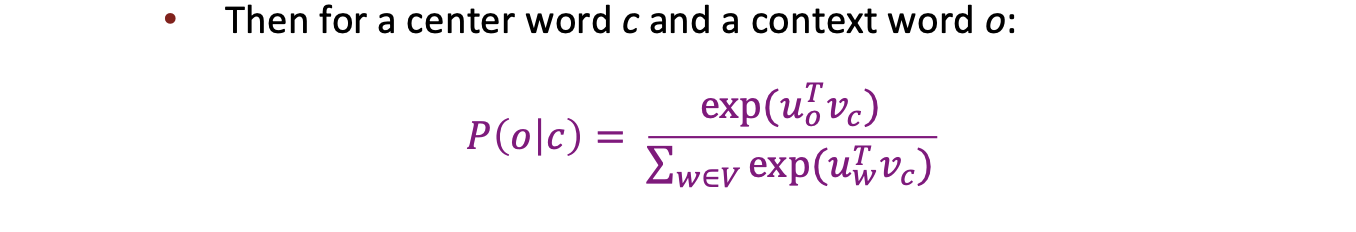
이 확률이 왜 이런 공식이 되었냐면...
- 분자: 문맥단어와 중심단어의 유사성을 비교하기 위해서 내적을 한다.
- 분자: 내적은 음수가 될 수 있지만 확률은 음수가 되면 안되기 때문에 지수함수를 취한다.
- 분모: 확률 분포를 만들기 위해 모든 단어에 대한 정규화를 한다.
이 구조는 소프트맥스 함수와 동일한 구조이다.
softmax function
소프트맥스 함수는 어떤 Rn의 벡터를 0과 1사이의 값으로 변환하는 것이다.임의의 값을 확률 분포에 매핑한다.
Optimization
모델학습 : 손실을 최소화하기위해서는 매개변수를 최적화해야한다.
- grdient를 내려가면서 parameters를 최적화해야한다.(경사하강법)
- 모든 벡터의 기울기를 계산해야한다!
그래서 이 교수님은 아까 prediction function를 중심단어 벡터에 대한 편도함수를 계산한다... 직접...
모든 수식을 여기에 옮겨적을 수 없으니 직접 받아 적은 노트를 업로드한다.
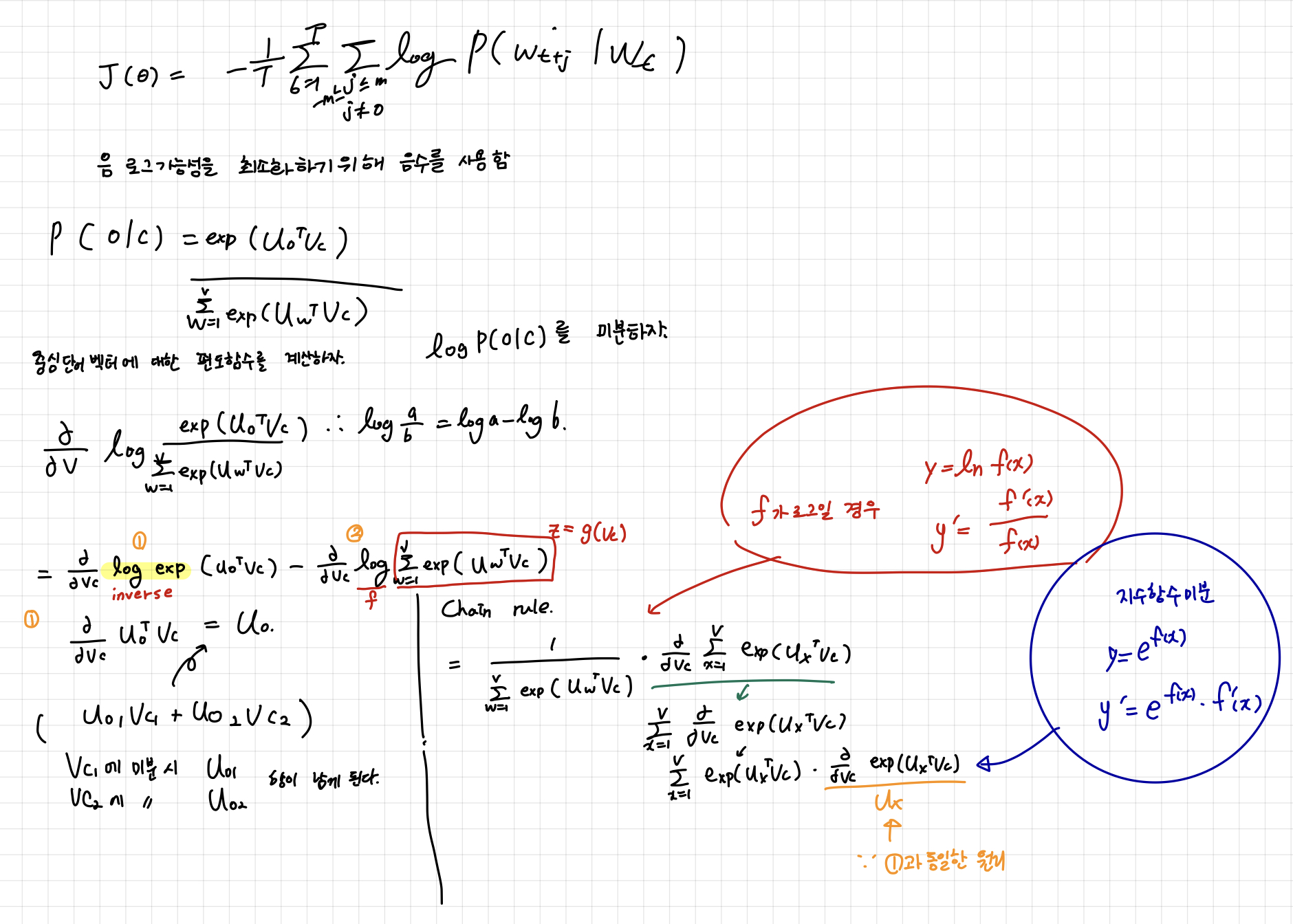
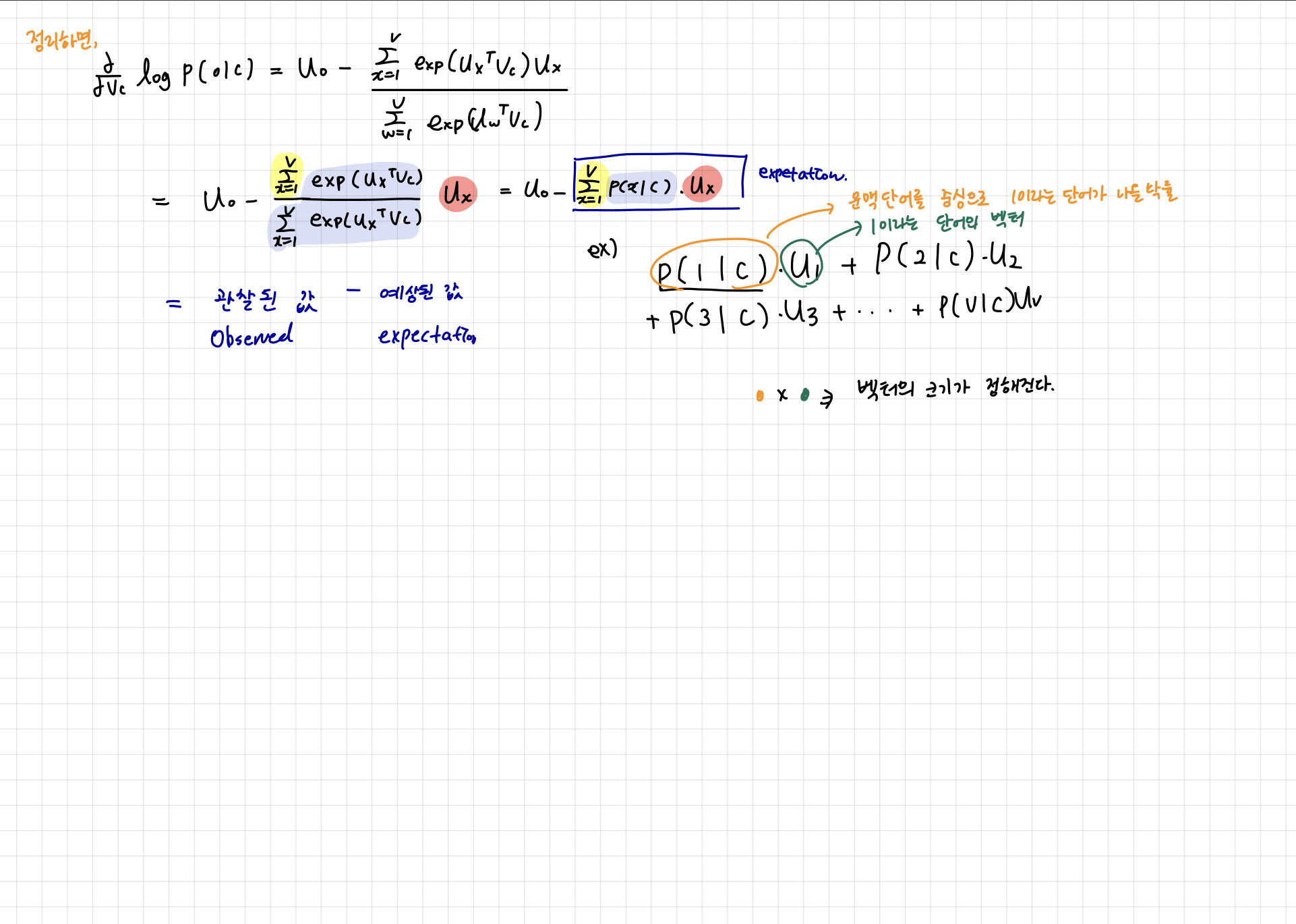
결국 관찰된 값에서 예상된 값을 뺀 것이 편도함수의 의미이다.
강의에서는 설명하지 않았지만 뇌피셜로 추가해서 적는다면,
이미 관찰된 값에서 예상된 값을 뺀 값이 0에 가까울 수록 최적화가 된 것이다. 예상된 값은 문맥단어를 중심으로 계산하는데, 이러한 문맥단어를 중심으로 모든 단어의 조건부확률과 단어의 벡터를 곱한 것의 합이다. 따라서 문맥단어가 중심단어와 유사하면 유사할 수록 예상된 값(벡터들의 합)은 중심단어의 벡터와 비슷해진다.
지금 까지 한 강의는 모두 Skip-Grams 알고리즘을 설명한 것이다.
Word2Vec에는 두가지 알고리즘이 있는데 그중 지금까지 배운 SG는 중심 단어를 통해 문맥 단어들을 예측하는 것이다.
사실 아리까리한 부분들이 많다. 왜 경사하강법을 사용하여 최적화 해야하고,
Lecture 2
이전 내용을 복습하고, 저번 내용에 살을 더 붙이는 방법으로 수업이 진행되었다.
Gradient Descent
바깥단어와 중심단어의 내적을 통한 모델은 bag of words model로 실제로 단어 순서나 위치에 전혀 상관없는 모델이고 이는 조잡한 언어 모델이다.
그에 반해 Word2Vect은 비슷한 단어를 공간상에 근처에 위치하게 끔한다.
그림은 2차원으로 표시되어 눈에 보이게 나타내지만, 사실은 더욱 고차원 공간에서 벡터를 표시한다.

이전 강의에서도 말했듯 우리는 좋은 단어 벡터를 배우기 위해서는 손실함수를 최소화해야하고 경사 하강법(Grdient Descent)를 통해 손실함수를 최소화할 수 있다.
여기서 경사 하강법은 함수의 최소값을 찾는 데 사용되고 주어진 함수가 파라미터에 대해 미분 가능할 때 유용하다.
- 파라미터 초기값을 선택하여 임의로 초기화한다.
- 경사를 계산한다.
- 경사 계산을 통해 얻은 기울기 정보를 사용해 현재 파라미터를 수정한다. 아때 기울기가 가장 크게 증가하는 방향 (기울기가 가장 큰 음의 방향)으로 파라미터를 이동한다.
- 일정한 조건이 만족될 때까지 반복한다.
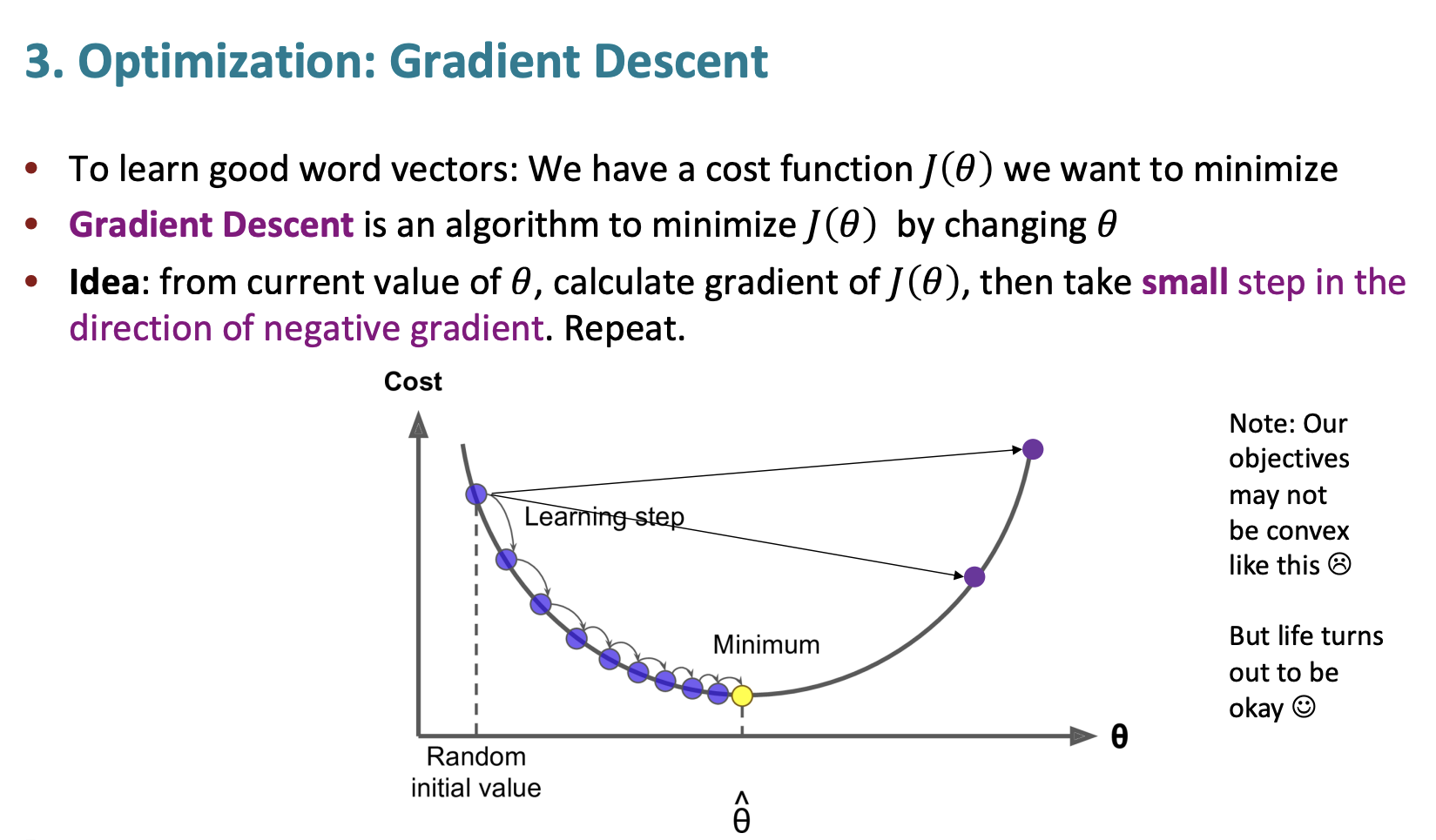
여기서 step size가 꽤나 중요한데, 만약 너무나도 작으면 계산하는데 시간과 비용이 커지게 되지만 너무 크게되면 최적값을 찾을 수 없게 된다.
경사 하강법의 방정식은 다음과 같다.
Update equation

그런데 경사하강법의 문제점이 있다. 모든 단어에 대해 계산을 한다면 너무너무너무 계산할 때 비싸진다. 전체 단어 코퍼스에서 진행하기 때문에 시간도 오래걸린다는 단점이 있다.
따라서 우리는 Stochastic gradient descent(SGD)를 사용한다.
이는 확률적 경사하강법이고 하나의 중심단어 또는 중심단어와 같은 small batch를 선택하여 업데이트를 진행하는 것이다. 이에 단점은 작은 부분만 보기 때문에 매우 noisy and bad하지만 계산이 빠르다는 장점이 있다.

하지만 이것도 window가 너무 작다면 확률 경사의 값이 너무나 sparse 하다는 단점을 가지고 있다.
Word2vec algorithm
일단 왜 두 벡터를 사용하는가? 에 대한 의문이 있을 수 있다. 단어당 하나의 벡터만 사용해서 word2vec 알고리즘을 구현할 수 있고 실제로 유용하다. 하지만 문맥을 파악할 때 알고리즘이 더욱 복잡해지기 때문에 2개의 벡터로 나눠 사용한다.
W2V 에는 두가지 알고리즘이 있다.
- Skip-grams: 주어진 중심 단어를 통해 문맥(outside)단어를 예측하는 것이다.
=> 지금까지 배운 내용이다. - Continuous Bag of Words(CBOW) : 문맥 단어 모음집에서 중심단어를 예측하는 것이다.
서로 예측하는 단어가 반대됨을 알 수 있다.
우리는 추가적으로 training 할 때 유용한 방법을 배울 것이다. 바로 Negative Sampling이다. 우리는 지금까지 naive한 softmax를 배웠지만 이는 간단하지만 비싼 방법이다.
Negative Sampling

이전에 배운 Prediction function 을 보면 분모를 계산하는 비용이 큰 것을 알수 있다. 왜냐하면 모든 단어들에 같은 계산을 반복해야하기 때문이다.
메인 idea는 이진 로지스틱 회귀를 취하는 것이다!
overall objective function

위 함수를 설명하면 동시에 발생하는 두 단어의 가능성을 최대화하고 노이즈 단어에 대한 가능성은 최소화해야한다는 것이다.
우리는 k개의 negative 한 단어 샘플들을 가지고 있다. (단어 확률을 통해 구한다.) 그리고 진짜 outside한 단어에 대해서는 높은 확률을 가져야하고 랜덤한 단어 샘플들에 대해서는 낮은 확률을 갖는 것이 좋다.
그리고 unigram한 분포에 3/4승을 한다. 이러한 이유는 일반적인 단어와 희귀한 단어 사이의 차이를 줄이는 효과 때문이다.

SVD
co-occurrence
동시발생행렬은 어떻게 구할까?
만약 window=1 이고 3개의 문장이 주어졌다고 하자.
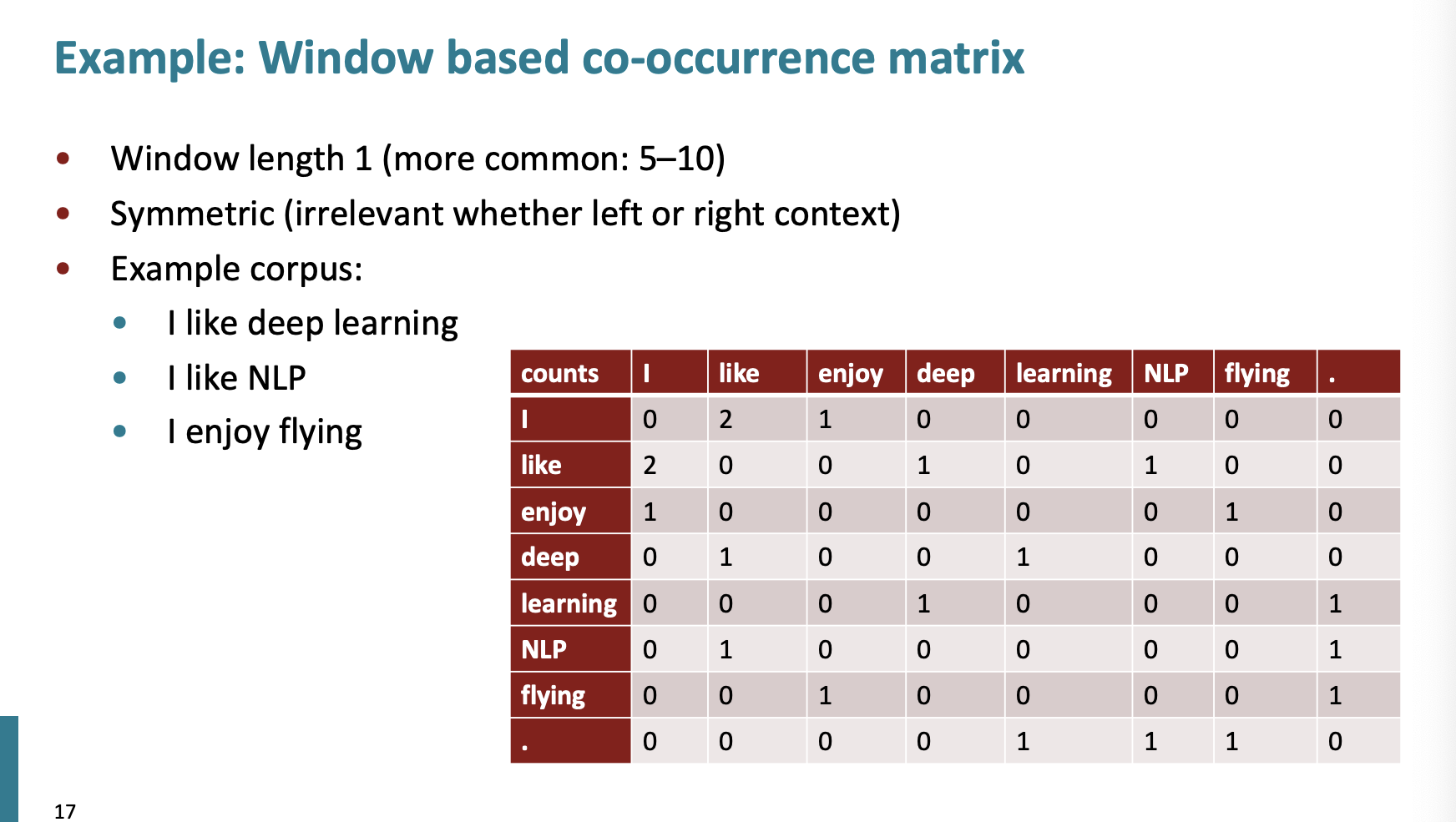
i like 는 2번 붙어있기에 2임을 확인할 수 있다.
순서는 상관없기에 행렬은 서로 대칭이다.
simple count co-occurrence vectors
간단하게 센다면 너무 고차원적이게 되고 큰 공간을 필요하게 된다.
그리고 희박성과 무작위성이 발생하여 모델이 less robust하게 된다는 단점이 있다.
low - dimensional vectors
그래서 이를 해결하기 위해 저차원에서 작업하면 더 나은 결과를 얻을 수 있음을 발견했다. 보통 25-1000차원을 사용한다.
그럼 어떻게 차원을 줄이는데..?
특이값 분해 방법
우리는 특이값 분해를 통해 모든 벡터에 대해 수행할 수 있다.
처음 k개의 특이값을 선택하여 차원을 줄인다.

즉 선택되지 않은 파란색 부분(특이값 선택x) , 노란색 부분(값이 없는 직사각형 빈공간)은 버리게 되어 차원을 줄일 수 있다.
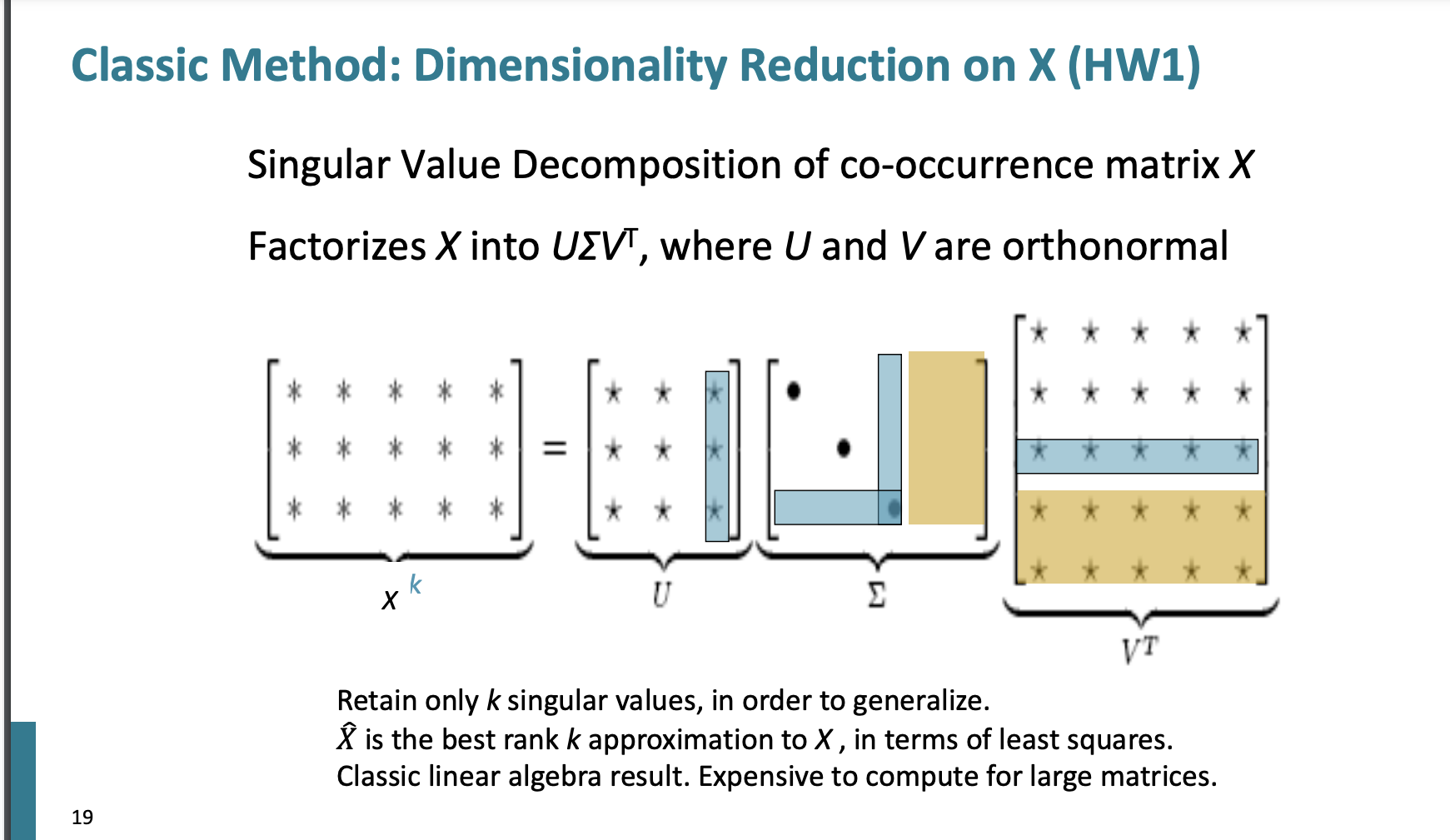
-> 특이값 분해 방법은 실제로 잘 수행이 되지 않고 계산도 해야할 게 많고 어쩌구 저쩌구 문제가 많다...
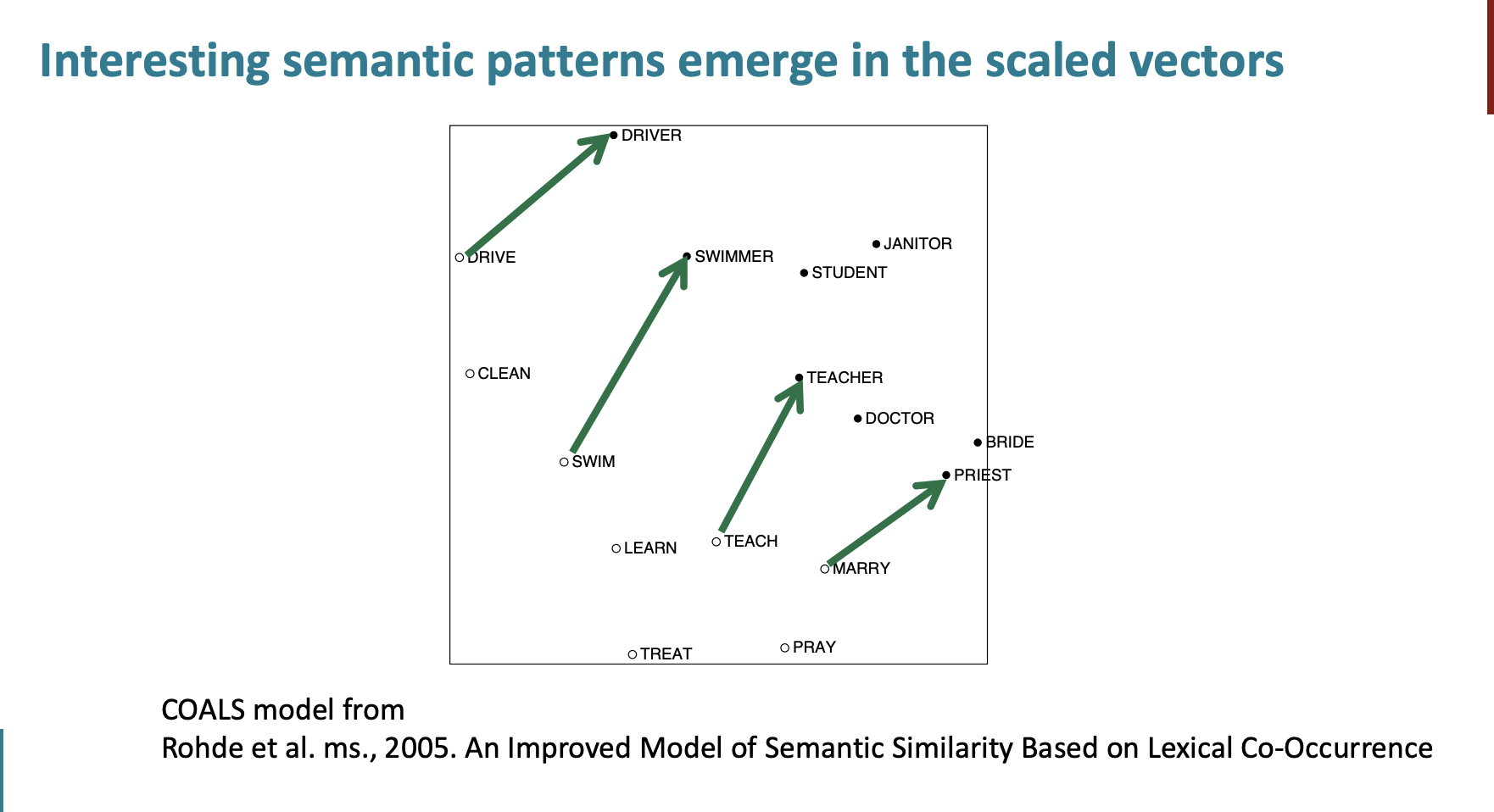
ps느낌으로 semantic patterns 에서 보이는 특징은
drive -> driver
swim -> swimmer
teach -> teacher
등의 벡터의 크기와 방향이 비슷하다는 것이다.
GloVe
일단 우리는 두가지 단어 임베딩 방법을 배웠다.
첫번째는 단어 개수와 행렬 분해에 의존하는 방법이다. 이는 빠르고 통계 정보를 잘 활용하지만 단어 유추에는 별로 좋지 않다.
두번째는 window 창 기반 방법이다. 이는 지역적인 문맥을 파악하고 단어 유사성을 넘어 복잡한 언어 패턴을 파악하지만 전체적인 동시발생 통계를 활용하지 못한다.
이를 해결하는 새로운 알고리즘 GloVe 에 대해 배워보자.
Global Vector for Word Representation의 약자로 단어 임베딩의 새로운 알고리즘이다.
이는 전역 단어 통계정보를 활용하고 벡터 공간을 만들어 단어 유추도 가능하게 한다.
통계정보 수집
일단 간단한 예시를 보자.
얼음은 고체와 물에 유사하다.
스팀은 가스와 물에 유사하다.
이를 나눠 계산한 결과는 다음과 같다.

손실함수 정의
벡터 공간에서 동시 발생한 확률의 비율을 선형적으로 캡처하는 방법은 ???

=> 두 단어 벡서 사이의 내적은 동시 발생 확률의 로그를 근사화하려고 시도한다..

내적(WiWj) 이 로그 발생(log Xij) 과 유사하길 원한다는 의미이다. 그리고 f 함수를 통해 높은 단어의 수를 제한 했다. 또한 제곱을 통해 양수를 취한다.
학습
GloVe는 신경 모델과도 유사하지만 동시발생행렬 모델의 사이라고 볼 수 있다.
손실 함수를 최소화하는 단어 벡터를 찾기위해 반복적으로 최적화 알고리즘을 사용한다.
Evalutaion
평가는 2가지 기준이 있다.
- 내재적 평가
-부분적으로 평가하는 것이다.
-계산이 빠르다.
-시스템을 이해하는데 도움을 준다.
- 외적 평가
-실제 작업을 통해 평가하는 것이다.
-시간이 오래 걸린다.
intrinsic word evaluation example
man -> woman 이면 king -> ???
???에는 queen이 나와야하는데 진짜 나오는건지 확인한다.
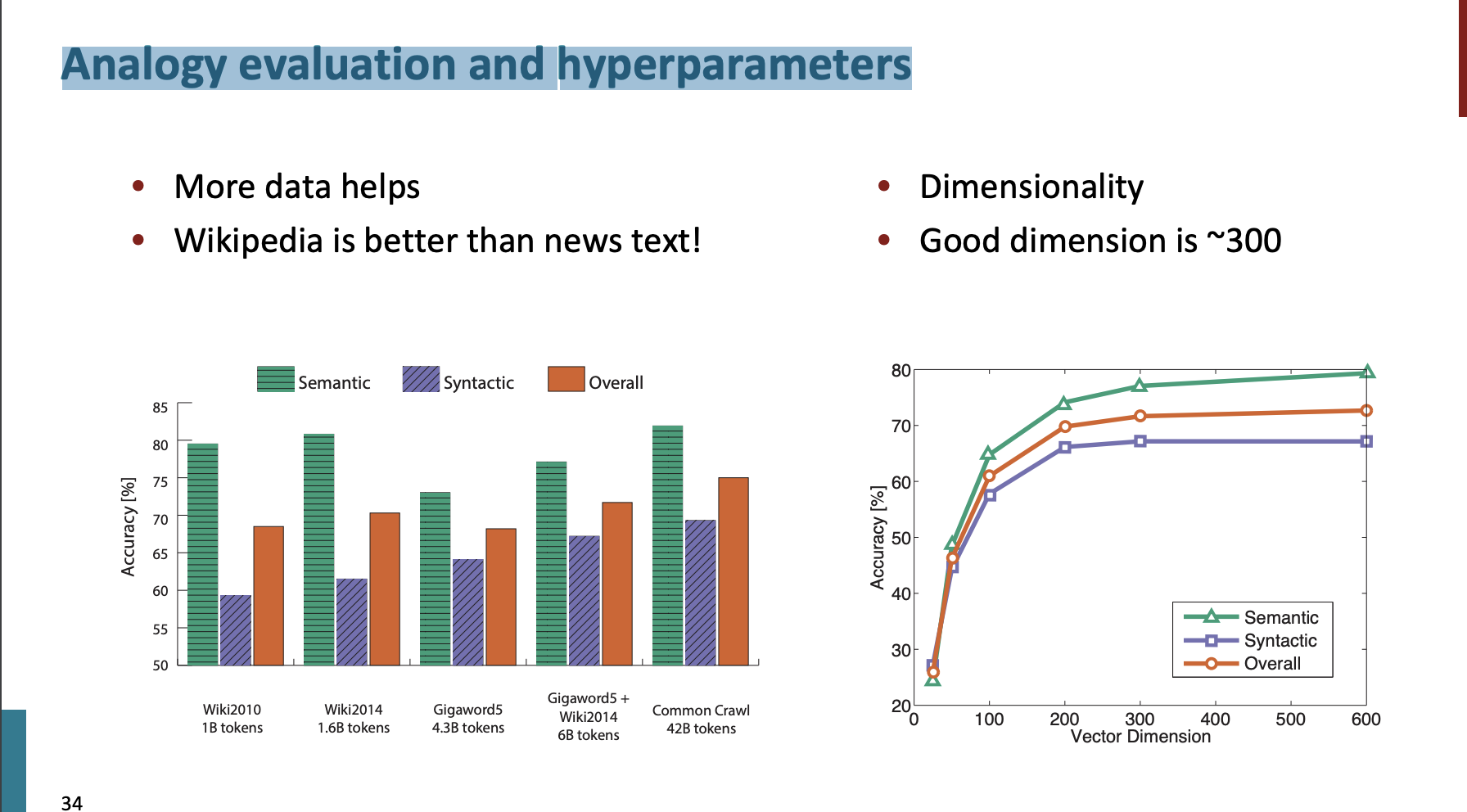
Analogy evaluation and hyperparameters
사실 많은 데이터가 좋은 결과를 낳는다.
뉴스 보다 위키피디아 데이터가 더 좋음을 확인했다.
또한 차원이 커질수록 더 좋다.
하지만 300이상의 차원은 크게 차이가 없음을 확인했다.
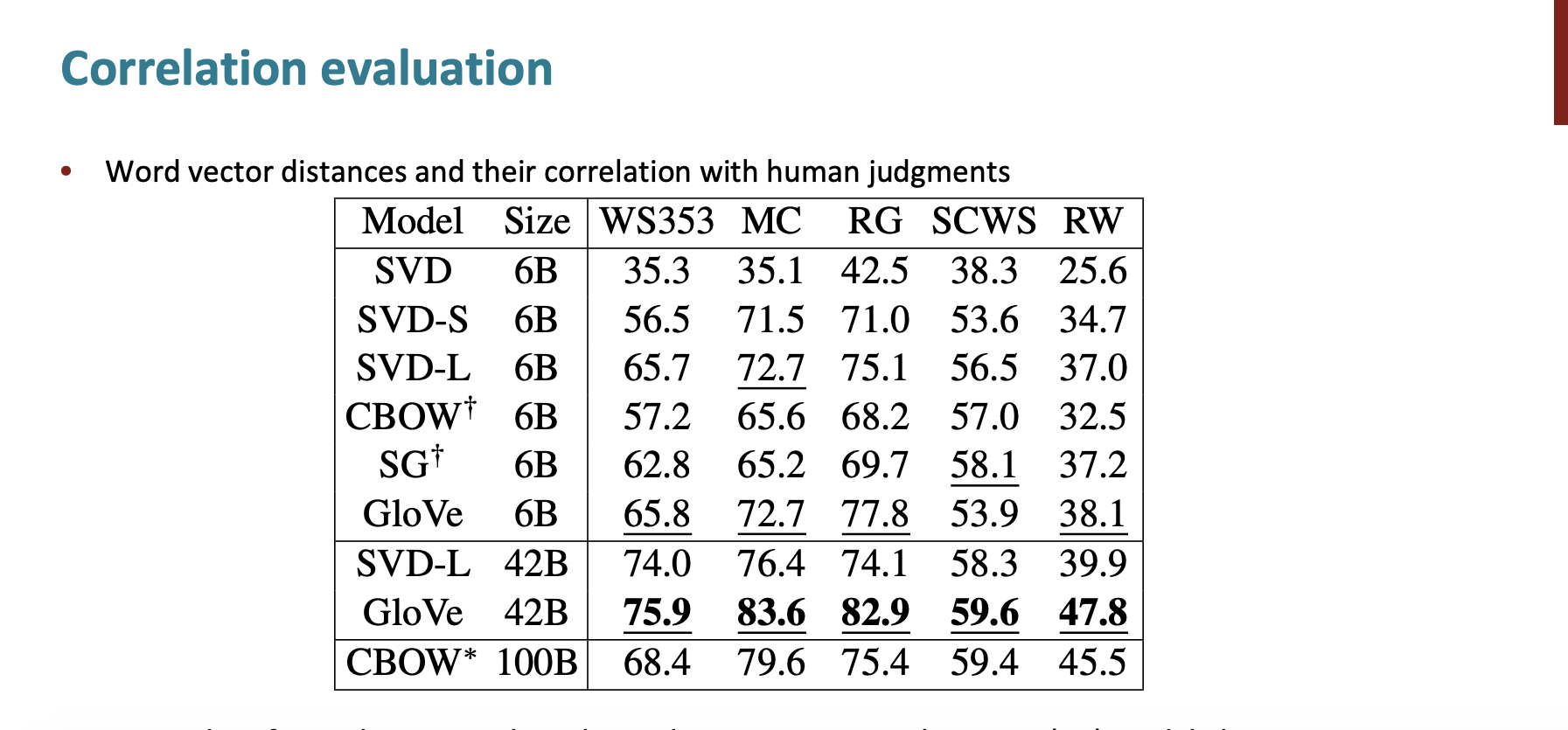
다른 intrinsic 방법은 직접 사람이 단어와 단어의 유사성에 대해 점수를 매기는 것이다.
그리고 correlation evaluation은 다음과 같았다.
Word sense and ambiguity
단어하나에 여러 의미를 가지고 있을 수 있다.
여기서는 pike라고 예시를 두었지만 한국어로 '머리'를 예시로 하면
명사
1. 사람이나 동물의 목 위의 부분. 눈, 코, 입 따위가 있는 얼굴을 포함하며 머리털이 있는 부분을 이른다. 뇌와 중추 신경 따위가 들어 있다.
머리를 긁다.
2. 생각하고 판단하는 능력.
머리가 나쁘다.
3. 머리에 난 털.
머리가 길다.
4. 한자에서 글자의 윗부분에 있는 부수. ‘家’, ‘花’에서 ‘宀’, ‘艹’ 따위이다.
5. 단체의 우두머리.
그는 우리 모임의 머리 노릇을 하고 있다.
6. 사물의 앞이나 위를 비유적으로 이르는 말.
장도리 머리 부분.
7. 일의 시작이나 처음을 비유적으로 이르는 말.
머리도 끝도 없이 일이 뒤죽박죽이 되었다.
8. 어떤 때가 시작될 무렵을 비유적으로 이르는 말.
해 질 머리.
9. 한쪽 옆이나 가장자리.
한 머리에서는 장구를 치고 또 한 머리에서는 징을 두드려 대고 있었다.
10. 일의 한 차례나 한 판을 비유적으로 이르는 말.
.. 등의 여러 의미를 가지고 있다.
이러한 의미를 모두 고려하여 10개의 단어 벡터로 나누게 되면 단어의 의미를 확실하게 나누는 것도 불완전하고 복잡하다는 단점이 있다.
그래서 "머리"라는 단어 벡터를 10개로 나누기보다는 모든 의미에 대한 알파값을 구하고 해당 의미 벡터와 알파값을 곱한 합을 벡터로 하는 것이다.
복잡한데 일단 공식을 보면 이해가 된다.

만약 3개의 의미를 가진 단어가 있다면 각단어의 알파를 구한다. f는 단어의 사용 빈도이다. 만약 첫번째 의미가 5, 두번째는 3, 세번째는 1 만큼 사용되었다면 첫번째 알파값은 5/9가 된다.
즉 사용횟수 만큼 벡터의 크기가 커지기 때문에 비례하여 해당 단어의 벡터에 의미에도 반영이 된다.
그리고 sparse coding을 통해 실제로 해당 의미를 분리할 수 있다고 결과가 나온다.. !!!
일단 여기까지 배웠고 다음 시간에 이어 나가자.. 수고 많았다 내자신!!!
