List에서 중복없이 Random하게 객체 뽑아내기

리스트에서 알고리즘 뽑아내기

리스트에서 랜덤하게 데이터를 중복없이 뽑아내는 방법은 어떤 것이 있을까? 우선 random을 활용해야 하고 다음과 같이 알고리즘을 짤 수 있다.

1. random 인스턴스를 생성한다.
2. random.nextInt(bound)를 활용해 인덱스로 접근할 랜덤한 정수 값을 받아온다.
3. 만약 이미 중복되어 있는지 체크하고 중복된다면 2번과정을 반복 수행한다.
4. 응답 리스트인 randomList에 random값을 추가한다.

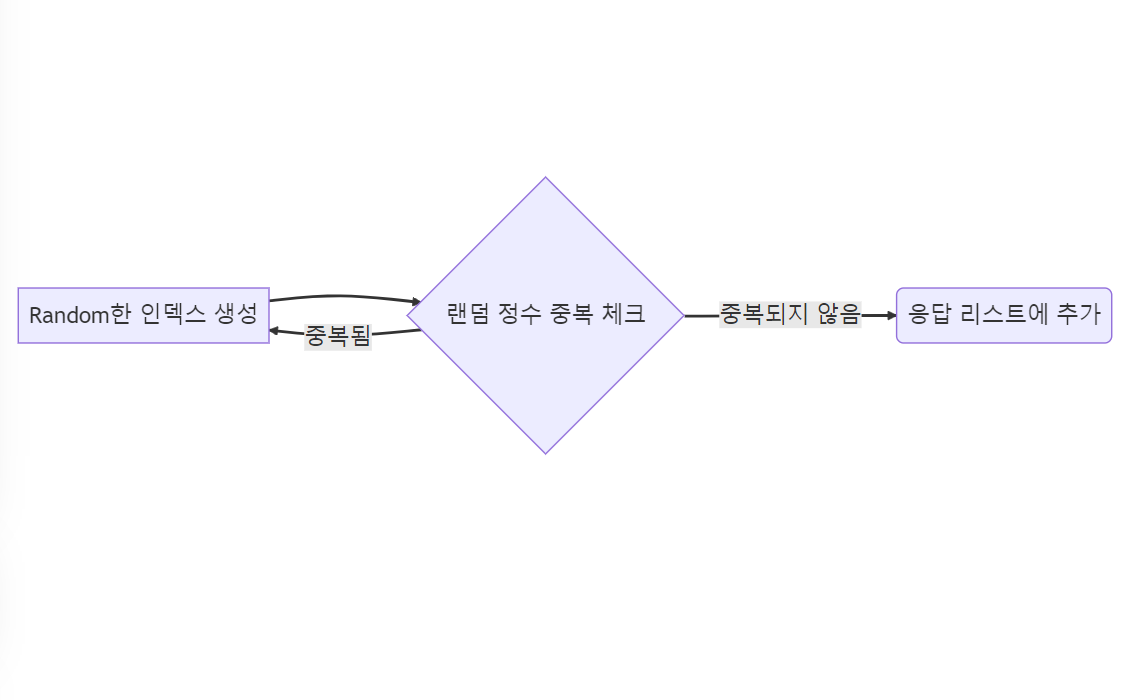
graph LR
A[Random 인스턴스 생성] --> B{랜덤 정수 중복 체크}
B -- 중복되지 않음 --> C(응답 리스트에 추가)
B -- 중복됨 --> A

static class RandomPicker {

        public static <T> List<T> randomPicker(List<T> data, int limit) {
            Random random = new Random();
            List<T> randomList = new ArrayList<>();
            for (int i = 0; i < limit; ++i) {
                int index = random.nextInt(data.size());
                if (randomList.contains(data.get(index))) {
                    continue;
                }
                randomList.add(data.get(index));
            }
            return randomList;
        }
    }

떠오르는대로 짯지만 이 코드는 문제가 있는 알고리즘이다. 그 이유는 뽑을때마다 중복되지 않게 뽑는 데 많이 뽑을 수록 중복되는 데이터가 많아지고 결국 중복안되는 데이터를 찾기 위해 엄청난 반복을 수행한다. O(N^2)이 걸릴수 있고 운이 안좋게 random 값이 잡히지 않는다면 사실상 거의 무한 반복할 가능성이 있다.

예를 들어보면 다음과 같다.

ex) 10만개의 리스트 데이터가 존재하는데 중복되는 인덱스를 뽑지 않기 위해 위의 알고리즘을 사용하면 0을 빼고 99999까지 모두 인덱스를 사용했다면 0을 뽑기 위해 해당 알고리즘은 무한 반복한다. 10만분의 1 확률로 0을 찾아야 하기 때문에 사실상 무한 반복에 가깝다.

또한 index만 중복되고 값은 중복되도 상관이 없는데 위 알고리즘은 Value Object나 원시 타입의 경우 값이 중복되도 무한 반복되므로 결과에 맞지 않는 결과를 리턴한다.

개선된 알고리즘

1. 0부터 size -1 까지 size만큼의 index 정보를 저장할 indices 배열을 만든다.
2. random한 정수를 (size - i) 만큼 크기를 bound로 가져온다.
3. 해당 인덱스의 data 값을 randomList에 추가하고 i번차에 도달할 수 있는 최대 indices 값과 선택한 indices의 값을 스왑한다.
4. 2번부터 3번 과정을 i가 limit에 도달할때까지 반복한다.

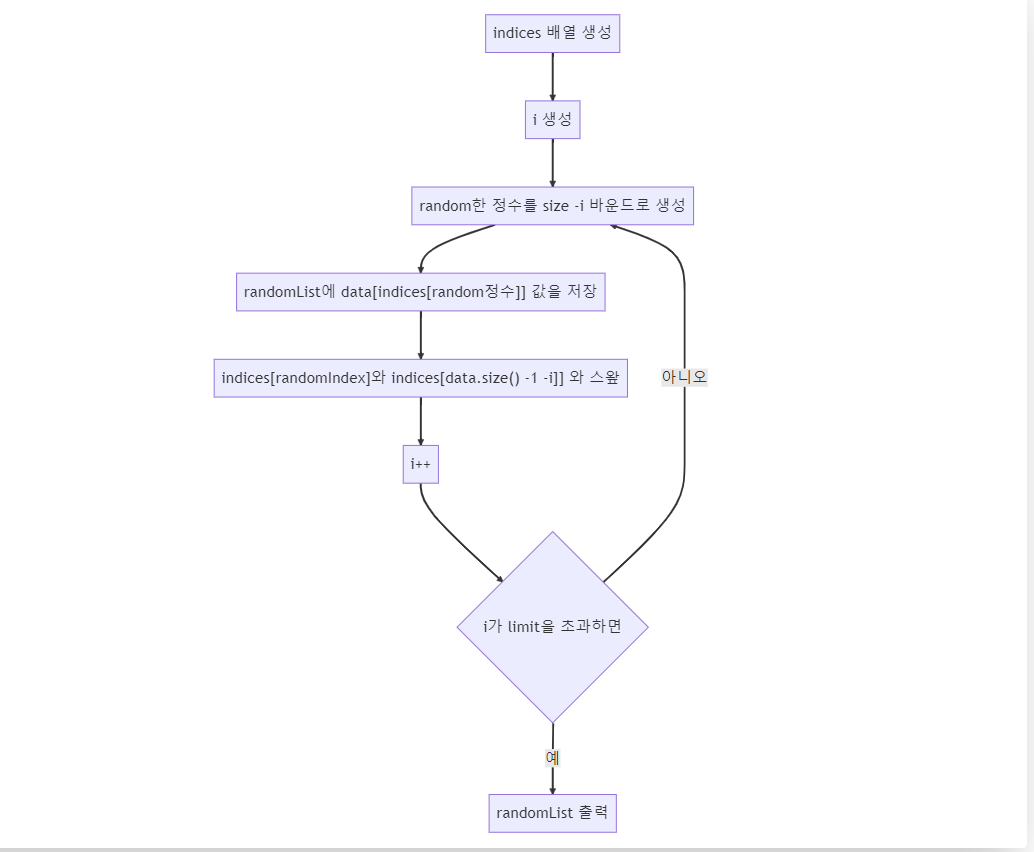
graph TD
A[indices 배열 생성 ]
B[i 생성]
C[i++]
D{i가 limit을 초과하면}
E[random한 정수를 size -i 바운드로 생성]
F["randomList에 data[indices[random정수]] 값을 저장"]
G["indices[randomIndex]와 indices[data.size() -1 -i]] 와 스왚"]
H["randomList 출력"]

A --> B
B --> E
E --> F
F --> G
G --> C
C --> D
D --아니오--> E 
D --예 --> H

	static class RandomPicker {

        public static <T> List<T> randomPicker(List<T> data, int limit) {
            Random random = new Random();
            int[] indices = IntStream.range(0, data.size()).toArray();
            List<T> randomList = new ArrayList<>();
            for (int i = 0; i < limit; ++i) {
                int randomIndex = random.nextInt(data.size() - i);
                randomList.add(data.get(indices[randomIndex]));
                indices[randomIndex] = indices[data.size() - 1 - i];
            }
            return randomList;
        }
    }

위 알고리즘의 차이점은 검사 로직이 없고 i가 증가할 떄마다 접근 가능한 indices의 max index는 size - i 만큼으로 줄어든다. 이 점을 이용해 random에서 선택한 index를 마지막 인덱스와 교환해줌으로써 중복을 해결하고 random bound가 줄어들면서 생성하기 때문에 충돌할 우려도 없다.

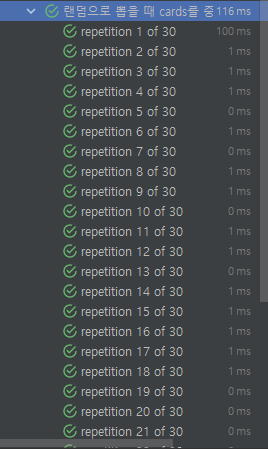
이전 알고리즘의 경우 10개 정도로 작은 데이터도 5초 넘게 걸렸는데 지금 알고리즘은 매우 junit 기준 53ms로 빠른 속도로 통과한다.

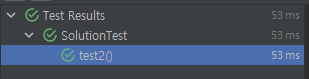
아마 junit 실행 동작 준비 과정 없이 로직만이라면 훨씬 빠른 속도가 나올 것이다.

랜덤한 카드 뽑기에 적용

카드를 랜덤으로 뽑는 작업을 어플리케이션 단에서 진행하고 코드를 짯는데 개선된 알고리즘을 베이스로 효율적으로 짤 수 있었다.

@Component
public class DefaultCardPicker implements CardPicker {

	@Override
	public List<Card> pickRandom(List<Card> cards, int limit) {
		if (cards.size() <= limit) {
			return new ArrayList<>(cards);
		}
		Random random = new Random();
		int[] indices = IntStream.range(0, cards.size()).toArray();
		List<Card> randomList = new ArrayList<>();
		for (int i = 0; i < limit; ++i) {
			int randomIndex = random.nextInt(cards.size() - i);
			randomList.add(cards.get(indices[randomIndex]));
			indices[randomIndex] = indices[cards.size() - 1 - i];
		}
		return randomList;
	}
}

테스트 속도는 다음과 같다.