[백준/C++] 17472번. 다리 만들기 2

[백준/C++] 17472번. 다리 만들기 2

1. 문제

섬으로 이루어진 나라가 있고, 모든 섬을 다리로 연결하려고 한다. 이 나라의 지도는 N×M 크기의 이차원 격자로 나타낼 수 있고, 격자의 각 칸은 땅이거나 바다이다.

섬은 연결된 땅이 상하좌우로 붙어있는 덩어리를 말하고, 아래 그림은 네 개의 섬으로 이루어진 나라이다. 색칠되어있는 칸은 땅이다.

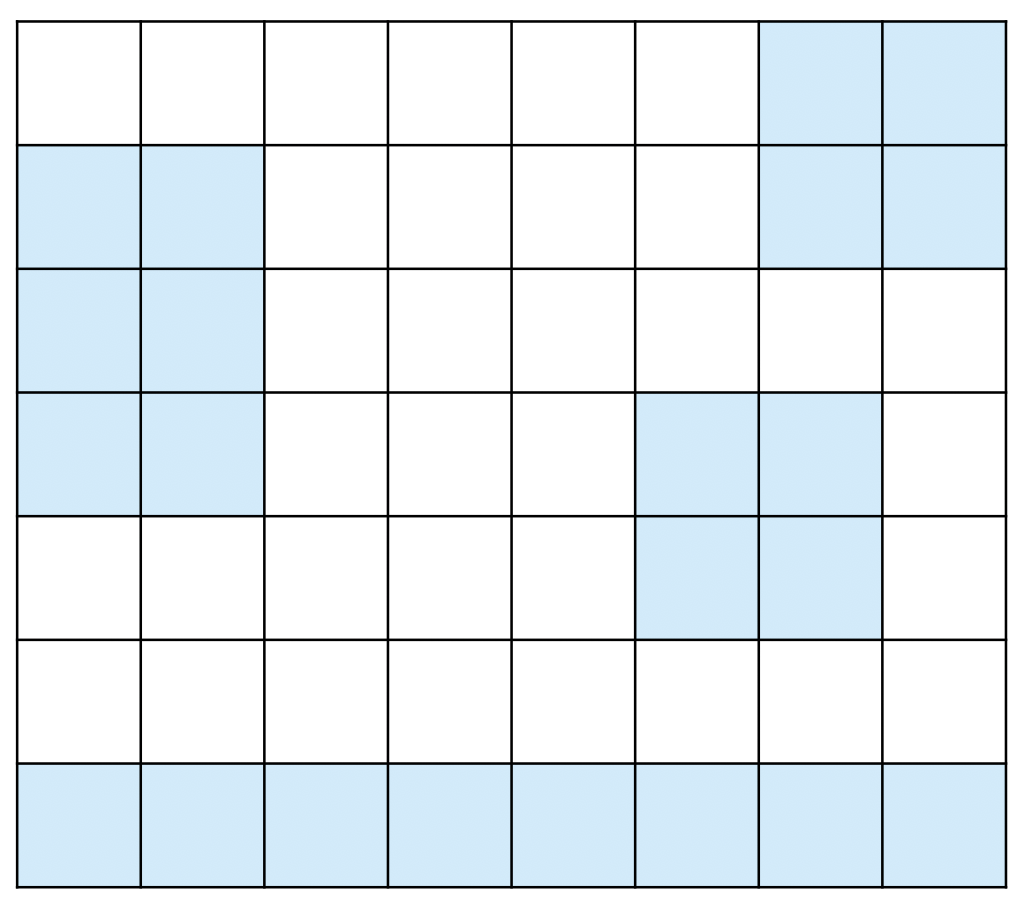
다리는 바다에만 건설할 수 있고, 다리의 길이는 다리가 격자에서 차지하는 칸의 수이다. 다리를 연결해서 모든 섬을 연결하려고 한다. 섬 A에서 다리를 통해 섬 B로 갈 수 있을 때, 섬 A와 B를 연결되었다고 한다. 다리의 양 끝은 섬과 인접한 바다 위에 있어야 하고, 한 다리의 방향이 중간에 바뀌면 안된다. 또, 다리의 길이는 2 이상이어야 한다.

다리의 방향이 중간에 바뀌면 안되기 때문에, 다리의 방향은 가로 또는 세로가 될 수 밖에 없다. 방향이 가로인 다리는 다리의 양 끝이 가로 방향으로 섬과 인접해야 하고, 방향이 세로인 다리는 다리의 양 끝이 세로 방향으로 섬과 인접해야 한다.

섬 A와 B를 연결하는 다리가 중간에 섬 C와 인접한 바다를 지나가는 경우에 섬 C는 A, B와 연결되어있는 것이 아니다.

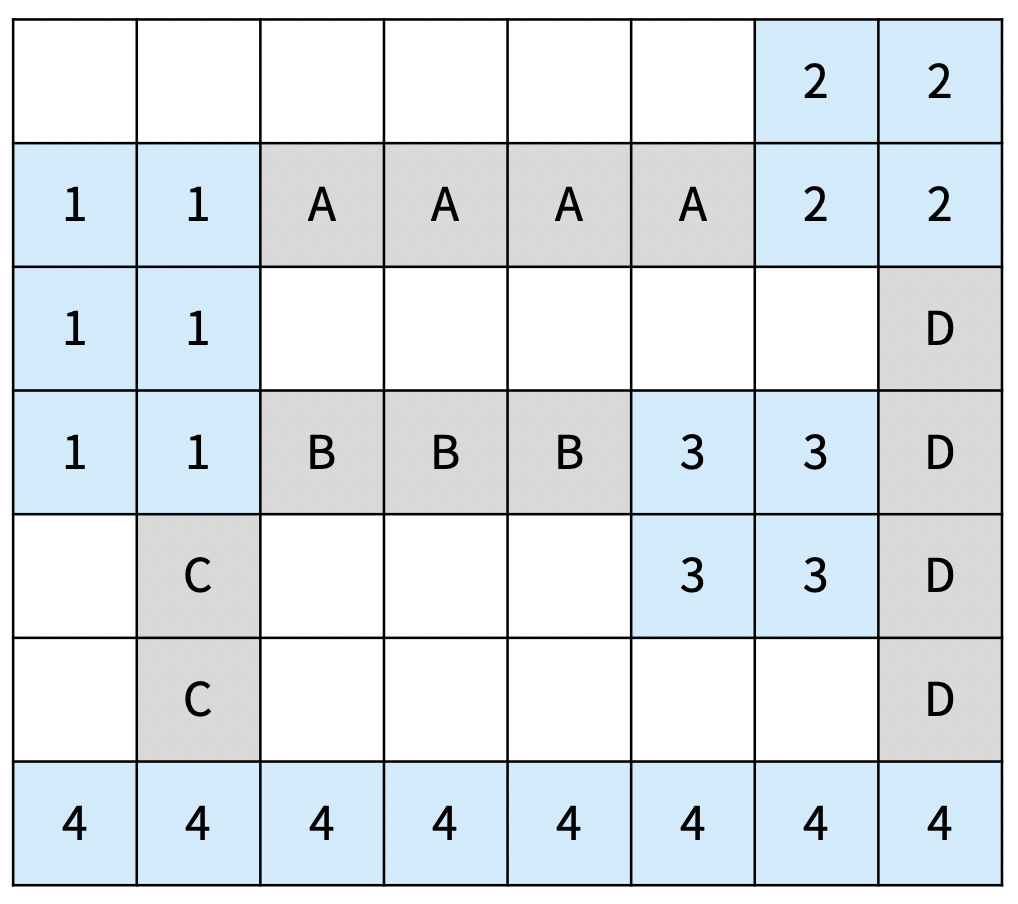
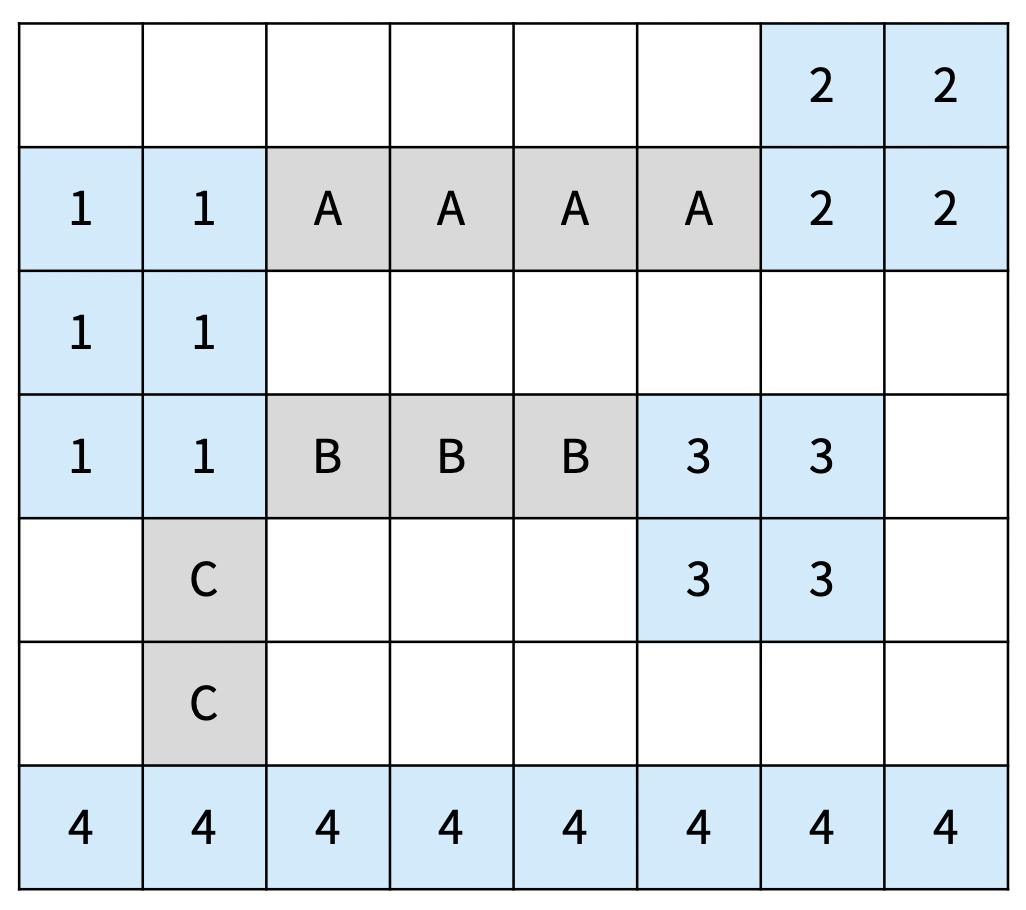
아래 그림은 섬을 모두 연결하는 올바른 2가지 방법이고, 다리는 회색으로 색칠되어 있다. 섬은 정수, 다리는 알파벳 대문자로 구분했다.

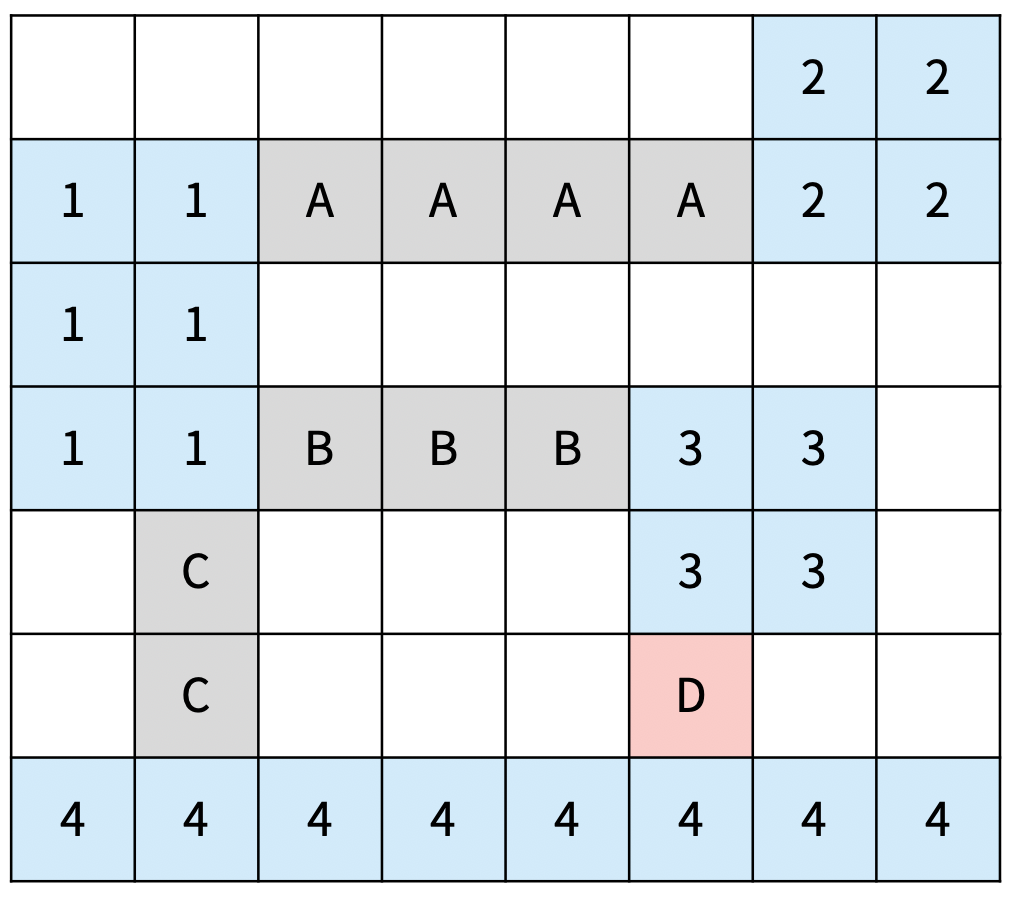
다리의 총 길이: 13 D는 2와 4를 연결하는 다리이고, 3과는 연결되어 있지 않다.	다리의 총 길이: 9 (최소)

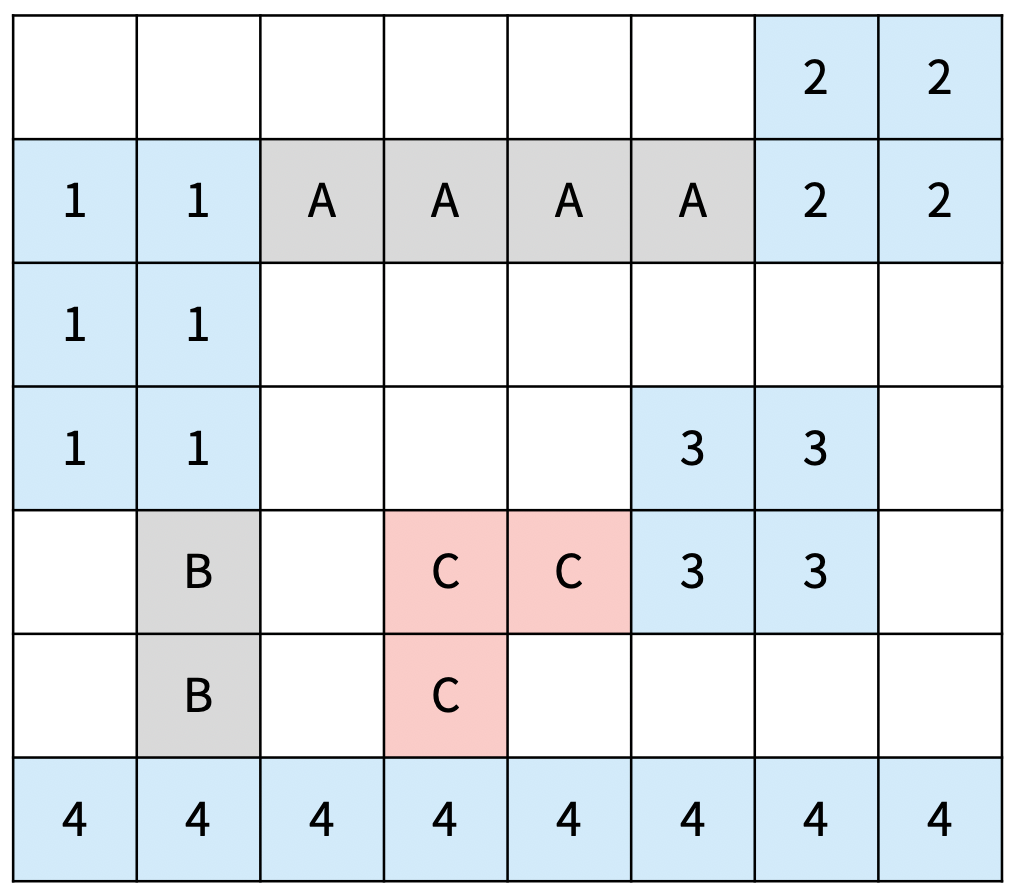
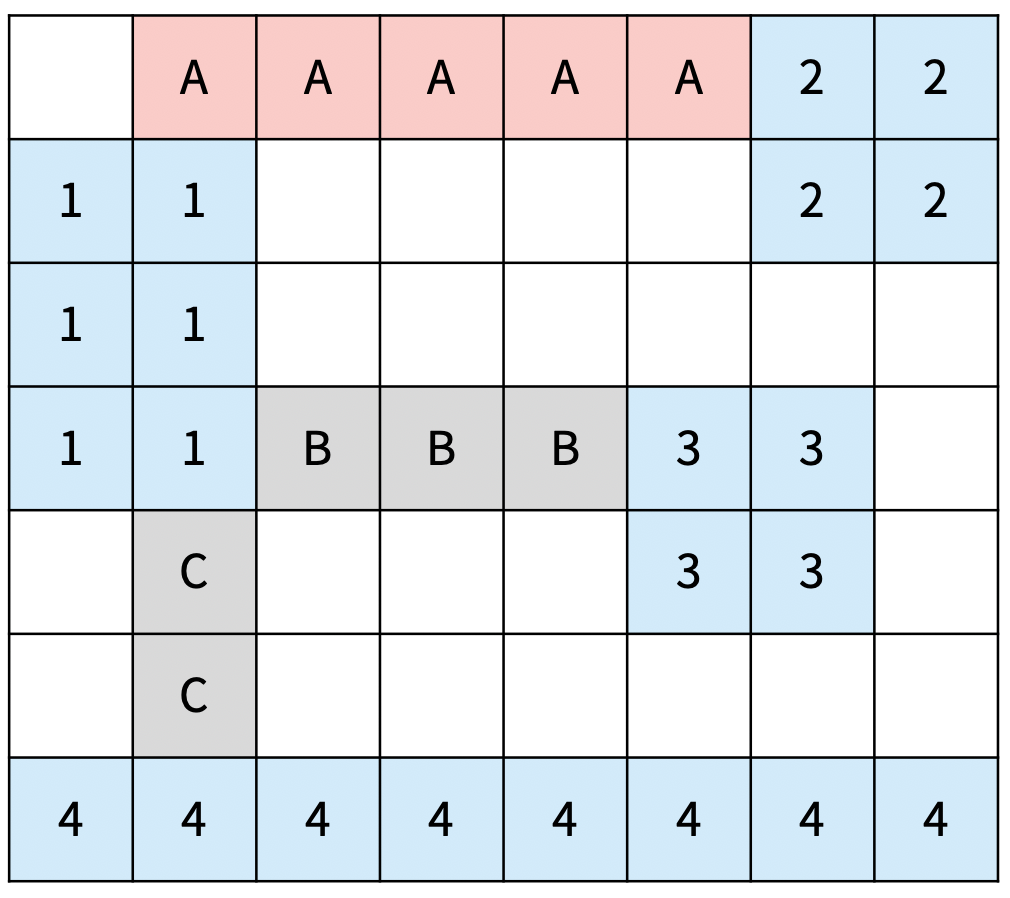
다음은 올바르지 않은 3가지 방법이다

C의 방향이 중간에 바뀌었다.	D의 길이가 1이다.	가로 다리인 A가 1과 가로로 연결되어 있지 않다.

다리가 교차하는 경우가 있을 수도 있다. 교차하는 다리의 길이를 계산할 때는 각 칸이 각 다리의 길이에 모두 포함되어야 한다. 아래는 다리가 교차하는 경우와 기타 다른 경우에 대한 2가지 예시이다.

A의 길이는 4이고, B의 길이도 4이다. 총 다리의 총 길이: 4 + 4 + 2 = 10	다리 A: 2와 3을 연결 (길이 2) 다리 B: 3과 4를 연결 (길이 3) 다리 C: 2와 5를 연결 (길이 5) 다리 D: 1과 2를 연결 (길이 2) 총 길이: 12

나라의 정보가 주어졌을 때, 모든 섬을 연결하는 다리 길이의 최솟값을 구해보자.

2. 입력

첫째 줄에 지도의 세로 크기 N과 가로 크기 M이 주어진다. 둘째 줄부터 N개의 줄에 지도의 정보가 주어진다. 각 줄은 M개의 수로 이루어져 있으며, 수는 0 또는 1이다. 0은 바다, 1은 땅을 의미한다.

3. 출력

모든 섬을 연결하는 다리 길이의 최솟값을 출력한다. 모든 섬을 연결하는 것이 불가능하면 -1을 출력한다.

4. 제한

• 1 ≤ N, M ≤ 10
• 3 ≤ N×M ≤ 100
• 2 ≤ 섬의 개수 ≤ 6

5. 풀이

참고자료

백준다리만들기 1
최소 스패닝 트리

• 섬들을 구분하는 DFS를 한다. 다리만들기 1 참고
• 섬에서 다른 섬으로 다리를 연결할 수 있는 모든 경우의 수를 vector에 추가한다.
  • 다리를 지을 수 있는 경우가 다리 만들기 1과 다르기 때문에 함수를 변경해주었다.
  • 특정 방향으로 이동하면서 지도 범위를 벗어나거나
  • 이동할 경로에 있는 땅이 출발 지점과 같으면 불가능을 리턴한다
  • 가능한 경우 경로와 다리가 연결될 땅을 묶어서 리턴한다.

pair<int, int> findRoute(int x, int y, int direction) {
  int land = map[x][y];
  int route = 0;

  while (true) {
    x += dx[direction];
    y += dy[direction];

    if (x < 0 || x >= n || y < 0 || y >= m) break;
    if (map[x][y] == land) break;

    if (map[x][y] != 0 && map[x][y] != land) return make_pair(route, map[x][y]);
    route++;
  }

  return make_pair(INF, -1);
}

• 모든 경우의 수를 비용 순으로 정렬해준다.
• 가장 적은 비용부터 하나씩 다리를 연결한다.
• 이 때 이미 연결된 땅은 연결하지 않는다.

  int totalCost = 0;
  for (int i = 0; i < v.size(); i++) {
    int cost = v[i].first;
    int a = v[i].second.first;
    int b = v[i].second.second;

    if (findParent(a) != findParent(b)) {
      unionParent(a, b);
      totalCost += cost;
    }
  }

• 모든 섬이 연결되었는지 확인하고 연결되었다면(=모든 섬의 부모가 같은지 확인한다.) 총 비용을 그렇지 않다면 -1을 출력한다.

6. 처음 코드와 달라진 점

• 다리 만들기 1처럼 현재 땅보다 번호가 큰 경우만 리턴하고 그렇지 않은 경우에는 다음으로 넘어갔는데 이렇게 하면 자기보다 번호가 작은 땅을 바다로 처리한다.
• 지나갈 수 없는 땅을 지나게 되는 문제가 생긴다.
• 수정 전

    if (map[x][y] > land) return make_pair(route, map[x][y]);

• 수정 후

    if (map[x][y] != 0 && map[x][y] != land) return make_pair(route, map[x][y]);

7. 코드

// 문제 및 풀이: https://velog.io/@e7838752/boj17472
#include <iostream>
#include <algorithm>
#include <queue>
#define INF 987654321

using namespace std;

int n, m;
int map[10][10];
int dx[] = {0, 1, 0, -1};
int dy[] = {-1, 0, 1, 0};
int parent[101];

void dfs(int x, int y, int land) {
  map[x][y] = land;

  for (int i = 0; i < 4; ++i) {
    int nx = x + dx[i];
    int ny = y + dy[i];

    if (nx < 0 || nx >= n || ny < 0 || ny >= m) continue;
    if (map[nx][ny] == 1) dfs(nx, ny, land);
  }
}

pair<int, int> findRoute(int x, int y, int direction) {
  int land = map[x][y];
  int route = 0;

  while (true) {
    x += dx[direction];
    y += dy[direction];

    if (x < 0 || x >= n || y < 0 || y >= m) break;
    if (map[x][y] == land) break;

    if (map[x][y] != 0 && map[x][y] != land) return make_pair(route, map[x][y]);
    route++;
  }

  return make_pair(INF, -1);
}

int findParent(int x) {
  if (x == parent[x]) return x;
  else return parent[x] = findParent(parent[x]);
}

void unionParent(int a, int b) {
  a = findParent(a);
  b = findParent(b);

  if (a < b) parent[b] = a;
  else parent[a] = b;
}

int main() {
  cin.tie(NULL);
  ios_base::sync_with_stdio(false);

  cin >> n >> m;
  for (int i = 0; i < n; ++i) {
    for (int j = 0; j < m; ++j) {
      cin >> map[i][j];
    }
  }

  for (int i = 2; i <= n * m; i++) {
    parent[i] = i;
  }
  

  int count = 2;
  for (int i = 0; i < n; ++i) {
    for (int j = 0; j < m; ++j) {
      if (map[i][j] == 1) {
        dfs(i, j, count++);
      }
    }
  }

  vector<pair<int, pair<int, int> > > v;
  for (int i = 0; i < n; ++i) {
    for (int j = 0; j < m; ++j) {
      if (map[i][j] > 1) {
        for (int k = 0; k < 4; ++k) {
          pair<int, int> p = findRoute(i, j, k);
          if (p.first == INF || p.first == 1) continue;
          v.push_back(make_pair(p.first, make_pair(map[i][j], p.second)));
        }
      }
    }
  }

  sort(v.begin(), v.end());

  int totalCost = 0;
  for (int i = 0; i < v.size(); i++) {
    int cost = v[i].first;
    int a = v[i].second.first;
    int b = v[i].second.second;

    if (findParent(a) != findParent(b)) {
      unionParent(a, b);
      totalCost += cost;
    }
  }
  
  bool isConnected = true;
  for (int i = 2; i < count; i++) {
    if (findParent(i) != findParent(2)) {
      isConnected = false;
      break;
    }
  }

  totalCost = isConnected ? totalCost : -1;
  cout << totalCost;
}