[백준] 2589번. 보물섬

[백준] 2589번. 보물섬

1. 문제

보물섬 지도를 발견한 후크 선장은 보물을 찾아나섰다. 보물섬 지도는 아래 그림과 같이 직사각형 모양이며 여러 칸으로 나뉘어져 있다. 각 칸은 육지(L)나 바다(W)로 표시되어 있다. 이 지도에서 이동은 상하좌우로 이웃한 육지로만 가능하며, 한 칸 이동하는데 한 시간이 걸린다. 보물은 서로 간에 최단 거리로 이동하는데 있어 가장 긴 시간이 걸리는 육지 두 곳에 나뉘어 묻혀있다. 육지를 나타내는 두 곳 사이를 최단 거리로 이동하려면 같은 곳을 두 번 이상 지나가거나, 멀리 돌아가서는 안 된다.

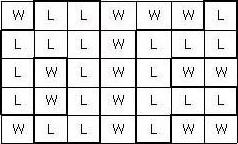
예를 들어 위와 같이 지도가 주어졌다면 보물은 아래 표시된 두 곳에 묻혀 있게 되고, 이 둘 사이의 최단 거리로 이동하는 시간은 8시간이 된다.

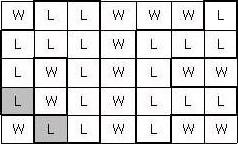
보물 지도가 주어질 때, 보물이 묻혀 있는 두 곳 간의 최단 거리로 이동하는 시간을 구하는 프로그램을 작성하시오.

2. 입력

첫째 줄에는 보물 지도의 세로의 크기와 가로의 크기가 빈칸을 사이에 두고 주어진다. 이어 L과 W로 표시된 보물 지도가 아래의 예와 같이 주어지며, 각 문자 사이에는 빈 칸이 없다. 보물 지도의 가로, 세로의 크기는 각각 50이하이다.

3. 출력

첫째 줄에 보물이 묻혀 있는 두 곳 사이를 최단 거리로 이동하는 시간을 출력한다.

4. 풀이

• 각 영역마다 'BFS'로 가장 멀리 떨어진 위치가 거리가 얼마인지 구해서 배열에 저장한다.
• 영역 중에 최댓값을 출력한다.

5. 처음 코드와 달라진 점

• 맨날 그렇듯이 push, pop을 빼 먹었다.

• 방문한 위치를 visited로 체크하지 않고 0인지 아닌지로 체크했다. 이 경우 시작점 또한 0이라서 시작점이 다시 2로 바뀐다. visited를 안 쓰고 싶으면 시작점을 1로 해야 했다. 근데 그냥 visited로 했다.

  2 2
  LW
  LW

• 라고 생각하면 최단 거리가 1이 나와야 하는데 2가 나온다.

6. 코드

#include <iostream>
#include <queue>
#include <algorithm>

using namespace std;

int n, m;
char map[50][50];
int route[50][50];
bool visited[50][50];
int d[50][50];

int dx[] = { 0,1,0,-1 };
int dy[] = { 1,0,-1,0 };

int bfs(int start_x, int start_y) {
    for (int i = 0; i < 50; i++) {
        for (int j = 0; j < 50; j++) {
            route[i][j] = 0;
            visited[i][j] = false;
        }
    }
        
    visited[start_x][start_y] = true;
    queue<pair<int, int>> q;
    q.push({ start_x, start_y });
    while (!q.empty()){
        int x = q.front().first;
        int y = q.front().second;
        q.pop();

        for (int i = 0; i < 4; i++){
            int nx = x + dx[i];
            int ny = y + dy[i];

            if (nx < 0 || nx >= n || ny < 0 || ny >= m) continue;
            if (map[nx][ny] == 'W') continue;
            if (!visited[nx][ny]) {
                visited[nx][ny] = true;
                route[nx][ny] = route[x][y]+1;
                q.push({ nx, ny });
            }
        }
    }

    int max_value = 0;
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            max_value = max(max_value, route[i][j]);
        }
    }
    return max_value;
}

int main(void) {
    cin.tie(NULL);
    ios_base::sync_with_stdio(false);

    cin >> n >> m;

    for (int i = 0; i < n; i++)
        for (int j = 0; j < m; j++)
            cin >> map[i][j];

    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            if (map[i][j] == 'L') d[i][j] = bfs(i,j);
        }
    }

    int answer = 0;
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            answer = max(answer, d[i][j]);
        }
    }
    cout << answer;
}