[프로그래머스/C++] 배달
1. 문제
N개의 마을로 이루어진 나라가 있습니다. 이 나라의 각 마을에는 1부터 N까지의 번호가 각각 하나씩 부여되어 있습니다. 각 마을은 양방향으로 통행할 수 있는 도로로 연결되어 있는데, 서로 다른 마을 간에 이동할 때는 이 도로를 지나야 합니다. 도로를 지날 때 걸리는 시간은 도로별로 다릅니다. 현재 1번 마을에 있는 음식점에서 각 마을로 음식 배달을 하려고 합니다. 각 마을로부터 음식 주문을 받으려고 하는데, N개의 마을 중에서 K 시간 이하로 배달이 가능한 마을에서만 주문을 받으려고 합니다. 다음은 N = 5, K = 3인 경우의 예시입니다.
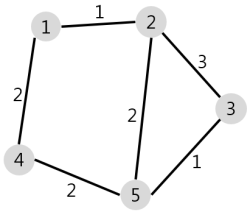
위 그림에서 1번 마을에 있는 음식점은 [1, 2, 4, 5] 번 마을까지는 3 이하의 시간에 배달할 수 있습니다. 그러나 3번 마을까지는 3시간 이내로 배달할 수 있는 경로가 없으므로 3번 마을에서는 주문을 받지 않습니다. 따라서 1번 마을에 있는 음식점이 배달 주문을 받을 수 있는 마을은 4개가 됩니다.
마을의 개수 N, 각 마을을 연결하는 도로의 정보 road, 음식 배달이 가능한 시간 K가 매개변수로 주어질 때, 음식 주문을 받을 수 있는 마을의 개수를 return 하도록 solution 함수를 완성해주세요.
2.제한사항
- 마을의 개수 N은 1 이상 50 이하의 자연수입니다.
- road의 길이(도로 정보의 개수)는 1 이상 2,000 이하입니다.
- road의 각 원소는 마을을 연결하고 있는 각 도로의 정보를 나타냅니다.
- road는 길이가 3인 배열이며, 순서대로 (a, b, c)를 나타냅니다.
- a, b(1 ≤ a, b ≤ N, a != b)는 도로가 연결하는 두 마을의 번호이며, c(1 ≤ c ≤ 10,000, c는 자연수)는 도로를 지나는데 걸리는 시간입니다.
- 두 마을 a, b를 연결하는 도로는 여러 개가 있을 수 있습니다.
- 한 도로의 정보가 여러 번 중복해서 주어지지 않습니다. - K는 음식 배달이 가능한 시간을 나타내며, 1 이상 500,000 이하입니다.
- 임의의 두 마을간에 항상 이동 가능한 경로가 존재합니다.
- 1번 마을에 있는 음식점이 K 이하의 시간에 배달이 가능한 마을의 개수를 return 하면 됩니다.
3. 풀이
다익스트라- 다익스트라 알고리즘으로 각 마을에 가는 최단 거리를 구한다.
4. 처음 코드와 달라진 점
- 양방향이라는 걸 고려하지 않았다.
5. 코드
#include <iostream>
#include <vector>
#include <queue>
#define INF 1e9
using namespace std;
int solution(int N, vector<vector<int> > road, int K) {
int answer=0;
vector<pair<int, int> > graph[51];
int d[51];
fill(d, d + 51, INF);
for(int i=0; i<road.size(); ++i) {
graph[road[i][0]].push_back({road[i][1], road[i][2]});
graph[road[i][1]].push_back({road[i][0], road[i][2]});
}
priority_queue<pair<int, int> > pq;
pq.push({ 0, 1 });
d[1] = 0;
while (!pq.empty()) {
int dist = -pq.top().first;
int now = pq.top().second;
pq.pop();
if (d[now] < dist) continue;
for (int i = 0; i < graph[now].size(); i++) {
int cost = dist + graph[now][i].second;
if (cost < d[graph[now][i].first]) {
d[graph[now][i].first] = cost;
pq.push(make_pair(-cost, graph[now][i].first));
}
}
}
for(int i=1; i<=N; ++i) {
if(d[i] <= K) answer++;
}
return answer;
}