[프로그래머스/CPP/JS] 스티커 모으기

[프로그래머스] 스티커 모으기

1. 문제

N개의 스티커가 원형으로 연결되어 있습니다. 다음 그림은 N = 8인 경우의 예시입니다.

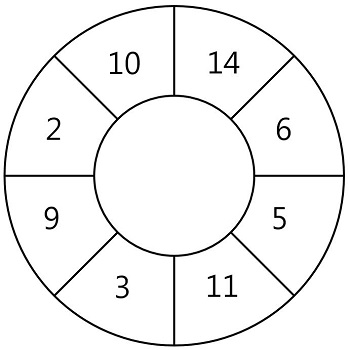
원형으로 연결된 스티커에서 몇 장의 스티커를 뜯어내어 뜯어낸 스티커에 적힌 숫자의 합이 최대가 되도록 하고 싶습니다. 단 스티커 한 장을 뜯어내면 양쪽으로 인접해있는 스티커는 찢어져서 사용할 수 없게 됩니다.

예를 들어 위 그림에서 14가 적힌 스티커를 뜯으면 인접해있는 10, 6이 적힌 스티커는 사용할 수 없습니다. 스티커에 적힌 숫자가 배열 형태로 주어질 때, 스티커를 뜯어내어 얻을 수 있는 숫자의 합의 최댓값을 return 하는 solution 함수를 완성해 주세요. 원형의 스티커 모양을 위해 배열의 첫 번째 원소와 마지막 원소가 서로 연결되어 있다고 간주합니다.

2. 제한 사항

• sticker는 원형으로 연결된 스티커의 각 칸에 적힌 숫자가 순서대로 들어있는 배열로, 길이(N)는 1 이상 100,000 이하입니다.
• sticker의 각 원소는 스티커의 각 칸에 적힌 숫자이며, 각 칸에 적힌 숫자는 1 이상 100 이하의 자연수입니다.
• 원형의 스티커 모양을 위해 sticker 배열의 첫 번째 원소와 마지막 원소가 서로 연결되어있다고 간주합니다.

3. 풀이

• 도둑질 문제랑 똑같은 문제다.
• 배열의 첫 원소를 포함하고 마지막 원소를 포함하지 않는 DP와 배열의 첫 원소를 포함하지 않고 마지막 원소를 포함하는 DP를 두 번 수행하여 최댓값을 리턴하면 된다.
• DP 점화식은 D[i] = max(D[i-1], D[i-2]+arr[i])
하나 전만 고를래? 두번 전이랑 지금 고를래?

4. 처음 코드와 달라진 점

• 오류 1 d2를 d1이라고 씀
  복붙하면 이런 실수를 참 많이 하는 것 같다.
• 오류 2 인덱스 잘못 씀
• 오류 3 배열의 길이가 1이나 2일수도 있는데 그냥 3개 이상이라고 가정하고 풀었다.
• 배열 이름이 d1, d2인 것도 참 맘에 안 들고 인덱스 접근 방식도 참 마음에 안 드는데 그냥 넘어가기로 했다.

5. 코드(CPP)

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

int solution(vector<int> sticker){
    int n = sticker.size();
    if(n==1) return sticker[0];
    if(n==2) return max(sticker[0], sticker[1]);
    
    vector<int> d1(n-1);
    vector<int> d2(n);
    
    d1[0] = sticker[0];
    d1[1] = max(sticker[0], sticker[1]);
    for(int i=2; i<n-1; i++){
        d1[i] = max(d1[i-1], d1[i-2] + sticker[i]);
    }
    
    d2[1] = sticker[1];
    d2[2] = max(sticker[1], sticker[2]);
    for(int i=3; i<n; i++){
        d2[i] = max(d2[i-1], d2[i-2] + sticker[i]);
    }
    int answer = max(d1[n-2], d2[n-1]);
    return answer;
}

6. 코드(JS)

function solution(sticker) {
  const len = sticker.length;
  if (len === 1) return sticker[0];
  if (len === 2) return Math.max(sticker[0], sticker[1]);

  const selectFirst = Array(len).fill(0);
  const selectLast = Array(len).fill(0);

  selectFirst[0] = sticker[0];
  selectFirst[1] = Math.max(sticker[0], sticker[1]);
  for (let i = 2; i < len - 1; i++) {
    selectFirst[i] = Math.max(selectFirst[i - 2] + sticker[i], selectFirst[i - 1]);
  }

  selectLast[1] = sticker[1];
  selectLast[2] = Math.max(sticker[1], sticker[2]);
  for (let i = 3; i < len; i++) {
    selectLast[i] = Math.max(selectLast[i - 2] + sticker[i], selectLast[i - 1]);
  }

  return Math.max(selectFirst[len - 2], selectLast[len - 1]);
}