[자료구조] Big-O 시간복잡도

Big-O :: exponential time

• 알고리즘의 성능을 수학적으로 표현해주는 표기법이다.

• 알고리즘의 시간과 공간 복잡도를 표현할 수 있다.

• Drop Constants
  알고리즘의 실제 러닝타임을 표시하는 것이 아닌,
  장기적으로 데이터가 증가함에 따른 처리시간의 증가율을 예측하기 위해서 만들어진 표기법이다.
  상수는 고정된 숫자이기 때문에 증가율에 영향을 미칠 때 언제나 고정된 상수만큼씩만 영향을 미친다.
  Big-O는 증가하지 않는 숫자는 신경쓰지 않기 때문에 상수와 같은 숫자들은 모두 1이 된다.

1. O(1) : Constant Time

• 입력 데이터의 크기에 상관없이 언제나 일정한 시간이 걸리는 알고리즘

function O_1(arr, idx) {
  return arr[idx] || -1;
}

2. O(n) : Linear Time

• 입력 데이터의 크기에 비례해서 처리 시간이 걸리는 알고리즘

function O_n(arr, num) {
  let result = 0;
  for (let i = 0; i < arr.length; i++) {
    if (arr[i] === num) {
      result = i;
      break;
    }
  }
  return result;
}

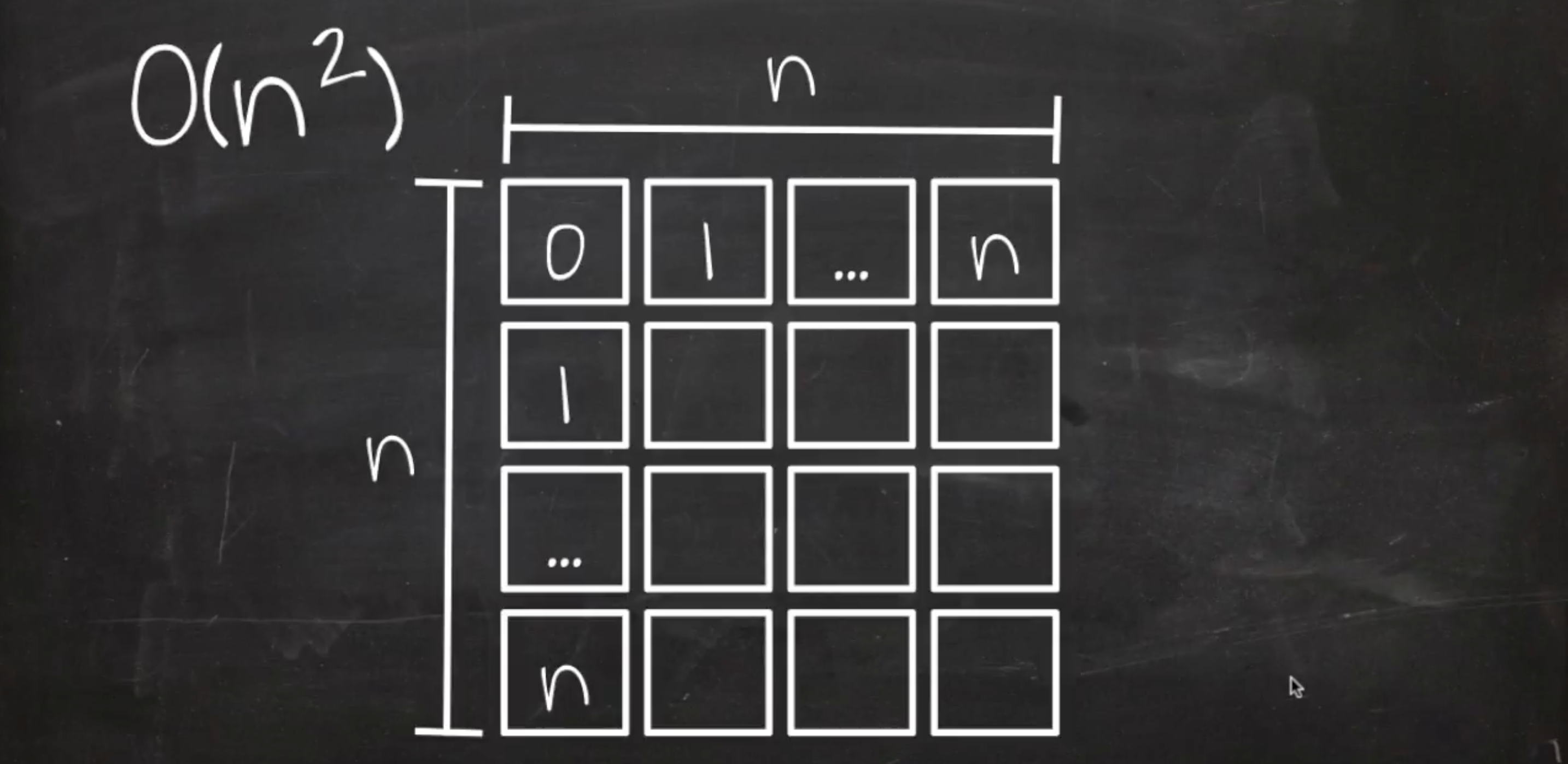
3. O(n^2) : Quadratic Time

• n을 돌리면서 그 안에서 n으로 루프를 또 돌리는 알고리즘

• n개의 데이터를 받으면 첫번째 루프에서 n번 돌면서 각각의 엘리먼트에서 n번씩 또 도니까
  처리 횟수는 n을 가로 세로 길이로 가지는 면적만큼 된다.

function O_n2(arr, num) {
  const result = [];
  arr.map((el, i) => {
    for (let l = 0; l < arr.length; l++) {
      if (i < l && i !== l && !result.includes(el + arr[l])) {
        result.push(el + arr[l]);
      }
    }
  });
  return result;
}

4. O(2^n)

• 값을 구하는 과정에서 2갈래로 나눠지는 트리 형태의 구조

피보나치 수열

• 함수를 호출할 때마다 바로 전의 숫자와 전전숫자를 알아야 더할 수 있기 때문에
  해당 숫자를 알아내기 위해서 하나 뺀 숫자를 가지고 재귀호출을 하고
  두개 뺀 숫자를 가지고 또 재귀호출을 한다.

• 이렇게 매번 함수가 호출될 때마다 두번씩 호출되고, 트리의 높이만큼 반복한다.

function O_2n(num) {
  if (num <= 1) return num;
  return O_2n(num - 2) + O_2n(num - 1);
}

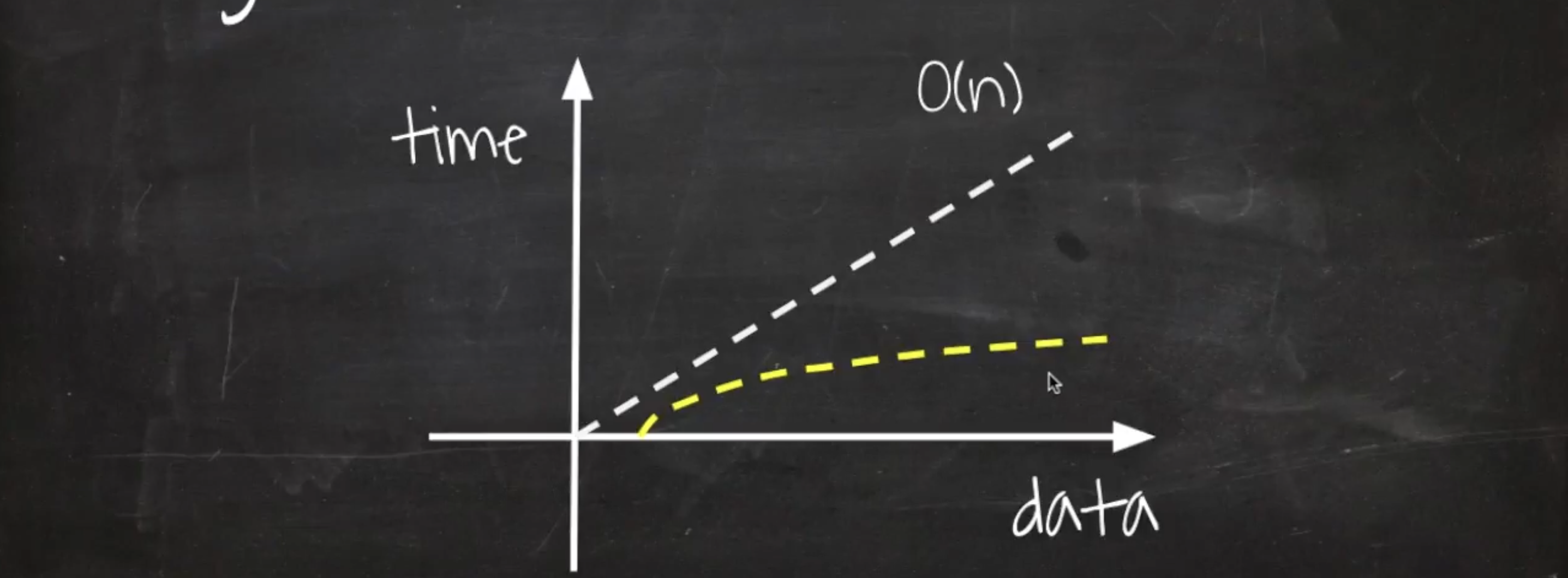
5. O(log n)

• O(n)을 일정한 횟수로 분할하여 문제를 풀이

이진 검색 binary search

1. 정렬된 데이터에서 가운데 값을 찾아서 찾으려는 값과 비교한다.
2. 찾으려는 값이 더 크면 앞의 데이터를 제거하고, 작으면 뒤의 데이터를 제거한다.
3. 남은 데이터의 중간 값과 다시 비교한다. 반복

• 한번 처리가 진행될 때마다 검색해야 하는 데이터의 양이 반으로 줄어드는 알고리즘
• 순차 검색과 비교했을 대 속도가 현저히 빠르다. 데이터가 증가해도 성능이 크게 차이 나지 않는다.

function O_log_n(arr, target) {
  let count = 0;
  arr = arr.sort((a, b) => a - b);
  let minIndex = 0;
  let maxIndex = arr.length - 1;
  while (minIndex <= maxIndex) {
    count++;
    const midIndex = Math.ceil((minIndex + maxIndex) / 2);
    if (arr[midIndex] < target) {
      minIndex = midIndex + 1;
    } else if (arr[midIndex] > target) {
      maxIndex = midIndex - 1;
    } else {
      return count;
    }
  }
  return -1;
}