SVM
서포트 벡터 머신의 메인 아이디어: 부류 간의 여백(마진)을 크게 하여 일반화 능력을 최대화
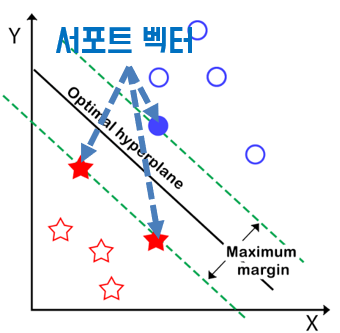
이를 위하여 결정함수와 목적함수를 이용한다.
결정함수를 이용하여 오류가 적거나(소프트 마진) 없는(하드 마진) 가중치 벡터(w)를 찾고,
목적함수를 이용하여 결정함수의 기울기(w)를 최적화하는 것이다.
선형 SVM
선형 SVM에서는 두 클래스를 분리하기 위하여 결정함수 를 이용한다.
결정함수
위 식은 특징공간을 2개로 분할하며 결정 초평면이라고도 부른다.
이 평면을 기준으로 한쪽 영역은 , 나머지 한쪽 영역은 으로 나눈다.
는 초평면의 법선 벡터이고, 바이어스()는 초평면의 위치를 지정한다.
- 임의의 점()에서부터 초평면까지의 거리()는 다음과 같이 나타낸다.
목적함수
목적함수는 마진을 가장 크게 하는 초평면의 기울기를 찾는 문제이다.
서포트 벡터에 대한 마진을 계산한 후 역수를 취하여 최솟값을 찾으면 최적의 값을 찾을 수 있다. 또, 에 상수 를 곱하여도 같은 초평면을 나타내므로 로 만들 수 있다.
-
서포트 벡터에 대한 마진은 다음과 같이 나타낼 수 있다.
= =
-
목적함수는 간단하게 아래와 같이 나타낼 수 있다.
선형 분리 불가능 문제
선형 분리가 불가능한 문제에서도 SVM을 적용할 수 있다.
아래와 같은 상황이 선형으로 두 클래스를 분리 시킬 수 없는 예이다.
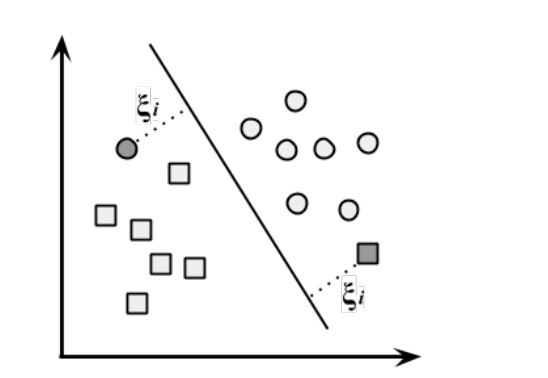
선형 SVM으로 이를 해결하려면 샘플 몇개정도는 마진안에 들어가는 것을 허용해야한다.
이를 허용하는 SVM을 소프트 마진 SVM이라고 한다.
훈련집합 ={}, ={}이고, ∈{1,-1}인 조건 하에서 최대 마진을 갖는 초평면을 찾는 것은 조건부 최적화 문제로 나타낼 수 있다.
라그랑주 승수법
조건부 최적화 문제는 라그랑주 승수법을 이용한다. 라그랑주 승수법의 기본 개념은 원문제(primal problem)의 등식제약을 함수의 제약으로 옮겨서 제약이 없는 문제로 표현하는 것이다. 이를 수식으로 표현하면 다음과 같다.
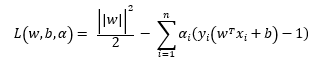
KKT 조건
하지만, 이문제는 부등식 조건하 최적화 문제이기 때문에 KKT 조건을 추가로 적용해야 한다.
- 라그랑주 함수 에서 라그랑주 승수를 제외한 로 편미분한 식이 0이다.
- 모든 라그랑주 승수()는 0보다 크거나 같다.
- 모든 조건식에 대해 이거나 이 되어야 한다.
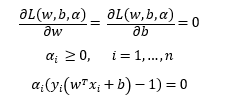
여기서 를 만족하는 점이 서포트 벡터이다.
쌍대 문제
지금까지 유도한 수식은 선형분류만 적용 가능하며, 비선형 문제를 해결하기 위한 커널 트릭을 적용하기 위해서는 쌍대문제를 이용해야 한다.
원문제가 이라는 조건 하에서 를 최소화하는 문제라고 하면,
쌍대문제는 과 이라는 두가지 조건하에서
를 최대화하는 문제로 표현할 수 있다.
위의 SVM문제를 쌍대문제로 나타낸다면 아래와 같이 표현할 수 있다.
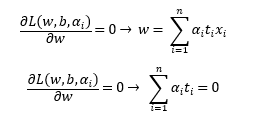
위 식을 에 대입하여 정리하면 아래와 같이 표현할 수 있다.
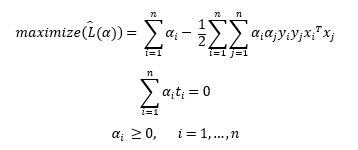
위의 식은 하나의 등식조건과 n개의 부등식 조건을 가진 2차 목적함수의 최대화 문제이다.
라그랑주 승수만 구한다면 와 를 구할 수 있을 뿐만 아니라 목적함수에서 특징벡터가 내적형태인 로 나타나기 때문에 머서의 정리를 이용하면 선형 SVM을 비선형 SVM으로 확장할 수 있다.
비선형 SVM
선형으로 분리되지 않는 데이터를 비선형 매핑, 즉 커널함수를 이용하여 해결할 수 있다.
머서의 정리를 이용하면 2차 다항식 매핑함수 φ를 이용하여 3차원 공간으로 매핑 시킬 수 있다.
머서(Mercer)의 정리
두개의 차원벡터 , 에 2차 다항식 매핑을 적용한 다음 변환된 벡터로 내적을 적용하면 아래와 같다.
즉, 변환된 벡터의 내적은 원래 백터의 내적의 제곱과 같다.
이를 이용하면 다양한 커널을 사용할 수 있다. 그 목록은 아래와 같다.
- 선형 :
- 다항식 :
- 가우시안 RBF :
- 시그모이드 :
참고문헌
[1] 기계학습(Machine Learning), 오일석, 한빛아카데미, 2016
[2] 인공지능(Artificial intelligence): 튜링 테스트에서 딥러닝까지, 이건명, 생능출판사, 2018
[3] 핸즈온 머신러닝 - 사이킷런, 케라스, 텐서플로 2를 활용한 머신러닝, 딥러닝 완벽 실무, Géron, A, 박해선, 한빛미디어, 2020