🥚문제

https://www.acmicpc.net/problem/11049

• 다이나믹 프로그래밍

---

🥚입력/출력

---

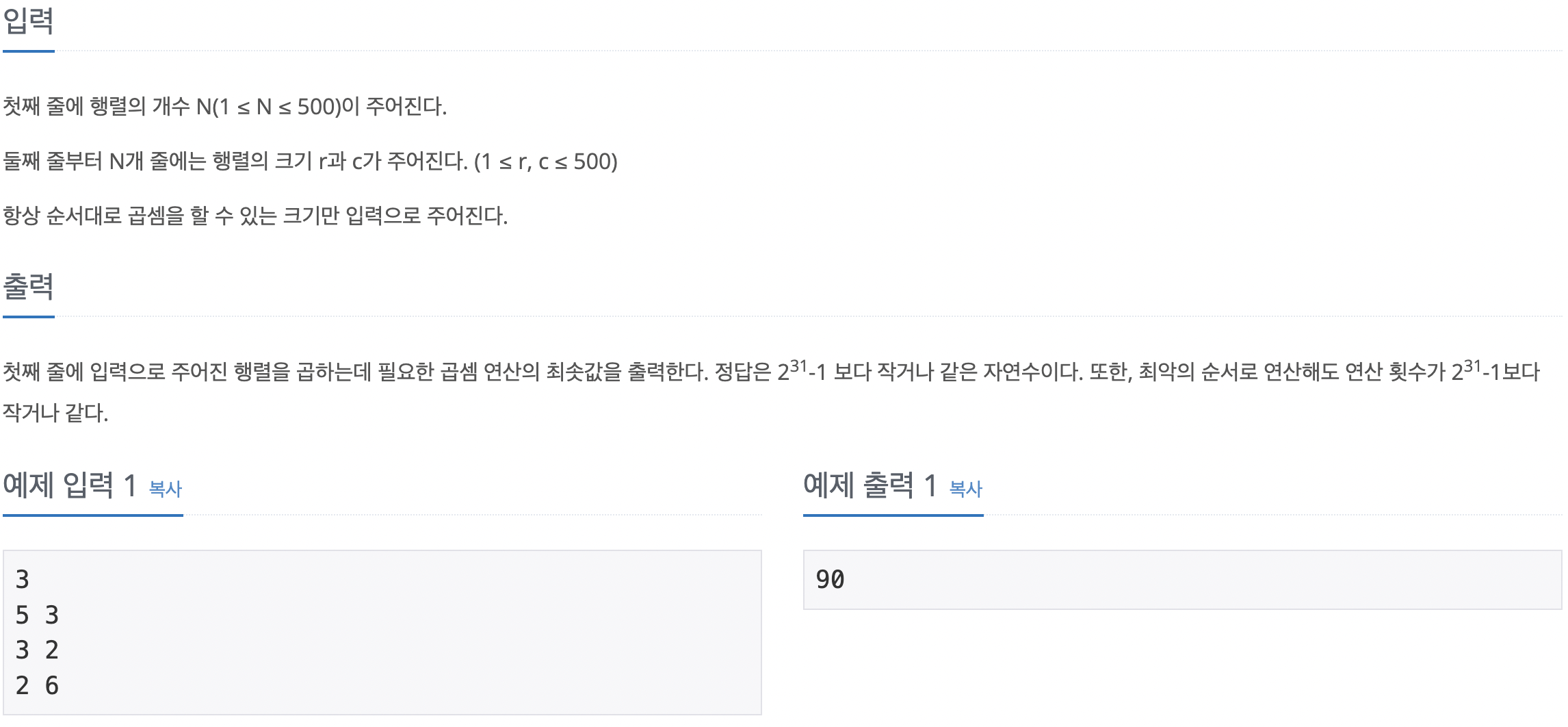
🍳코드

import sys
input = sys.stdin.readline

N = int(input())
matrix = []
for _ in range(N):
    matrix.append(tuple(map(int, input().split())))

# dp[i][j] = 행렬 i~j까지 곱했을 때, 곱셈 연산 횟수의 최솟값
dp = [[0]*N for _ in range(N)]
# 대각선↘︎으로 순회하며 값 채우기
for idx in range(1, N):
    for i in range(N):
        j = i + idx
        if j < N:
            if j == i+1:
                dp[i][j] = matrix[i][0] * matrix[j][0] * matrix[j][1]
            else:
                dp[i][j] = 2**31 - 1
                
                # (i~x) * (x~j)
                # A(BCD) | (AB)(CD) | (ABC)D
                for x in range(i, j+1):
                    if x == i:
                        dp[i][j] = min(dp[i][j], 
                        dp[i+1][j] + matrix[i][0]*matrix[i+1][0]*matrix[j][1])
                    elif x == j:
                        dp[i][j] = min(dp[i][j], 
                        dp[i][j-1] + matrix[i][0]*matrix[j][0]*matrix[j][1])
                    else:
                        dp[i][j] = min(dp[i][j],
                        dp[i][x] + dp[x+1][j] + matrix[i][0]*matrix[x+1][0]*matrix[j][1])

print(dp[0][N-1])

---

🧂아이디어

DP

• dp[i][j] = 행렬i ~ 행렬j까지를 곱셈했을 때, 곱셈 연산 횟수의 최솟값을 저장

• 행렬 4개가 주어지고 각각의 크기가 5*3, 3*2, 2*6, 6*4 일 때
  matrix = [(5, 3), (3, 2), (2, 6), (6, 4)]

• 위 입력을 이용하여 dp를 구성하면, 초기 dp의 상태는
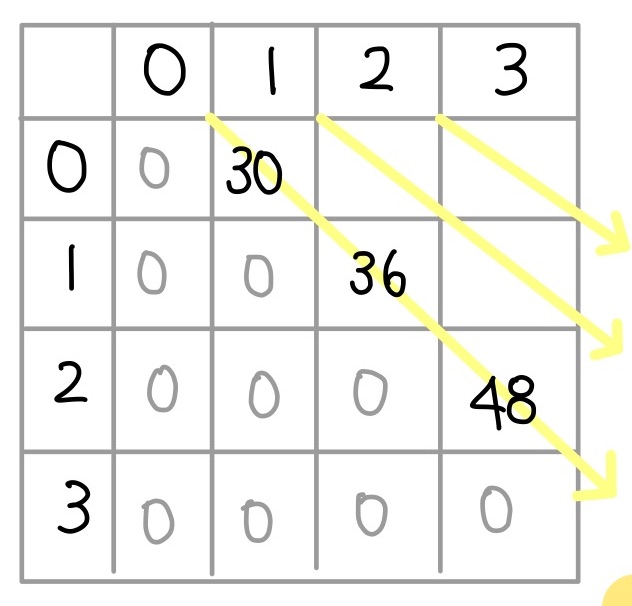
  • 모든 값을 0으로 초기화한 뒤
  • dp[i][i+1]의 값을 행렬i와, 행렬(i+1)의 곱셈 횟수로 업데이트해준다.
    dp[i][i+1] = matrix[i][0]*matrix[i+1][0]*matrix[i+1][1]

• dp를 대각선 방향(↘︎)으로 순회하며 나머지 값들을 갱신해준다.

• 만약 dp[0][3]을 구한다고 하면, 행렬0에서 행렬3까지 순서대로 곱셈하는 방법은 아래와 같다.
  • 행렬0 * (행렬1 행렬2 행렬3)
  • (행렬0 행렬1) * (행렬2 행렬3)
  • (행렬0 행렬1 행렬2) * 행렬3
  • 위 경우들 중 최소 곱셈 횟수가 dp[0][3]의 값이 된다.

• 따라서, dp[i][j] = 2**31 - 1 (문제에서 제시한 최대값)으로 둔 뒤,
  i <= x < j+1일 때 아래와 같은 식을 수행하면 된다.

if x == i:
    dp[i][j] = min(dp[i][j], 
    # (i+1) ~ j 까지의 최소 연산 횟수 + 행렬i와 행렬((i+1)~j)곱의 결과를 곱하는 횟수
    dp[i+1][j] + matrix[i][0]*matrix[i+1][0]*matrix[j][1])
elif x == j:
    dp[i][j] = min(dp[i][j],
    # i~(j-1) 까지의 최소 연산 횟수 + 행렬(i~(j-1))곱의결과와 행렬j를 곱하는 횟수
    dp[i][j-1] + matrix[i][0]*matrix[j][0]*matrix[j][1])
else:
    dp[i][j] = min(dp[i][j],
    # i~x까지의 최소 연산 횟수 + (x+1)~j까지의 최소 연산 횟수 + 행렬(i~x)곱의 결과와 행렬(x+1~j)곱의 결과를 곱하는 횟수
    dp[i][x] + dp[x+1][j] + matrix[i][0]*matrix[x+1][0]*matrix[j][1])

• 전체적인 아이디어 정리는 아래 그림