🥚문제

https://www.acmicpc.net/problem/5639

• 그래프 이론
• 그래프 탐색
• 트리
• 재귀

---

🥚입력/출력

---

🍳코드

import sys
input = sys.stdin.readline
sys.setrecursionlimit(10**6)

def pre_to_post(start, end):
    if start > end:
        return
    
    root = preorder[start]

    # root보다 커지는 인덱스 찾기
    idx = start
    while idx <= end:
        if preorder[idx] > root:
            break
        idx += 1
    
    # 왼쪽
    pre_to_post(start+1, idx-1)
    # 오른쪽
    pre_to_post(idx, end)
    # 루트
    print(root)


# 입력
preorder = []
while True:
    try:
        preorder.append(int(input()))
    except:
        # EOF -> break
        break

# pre_to_post
pre_to_post(0, len(preorder)-1)

---

🧂아이디어

그래프 이론

입력받기 😮

• 문제의 입력에서 노드의 개수, 혹은 입력 종료 조건이 주어지지 않았다.

• EOF입력 시 종료되어야 한다.

• 따라서, while loop 내부 try-except문을 이용하여 EOF시 입력 받는 루프를 빠져나오게 구성했다.

# 입력
preorder = []
while True:
    try:
        preorder.append(int(input()))
    except:
        # EOF -> break
        break

전위순회 -> 후위순회

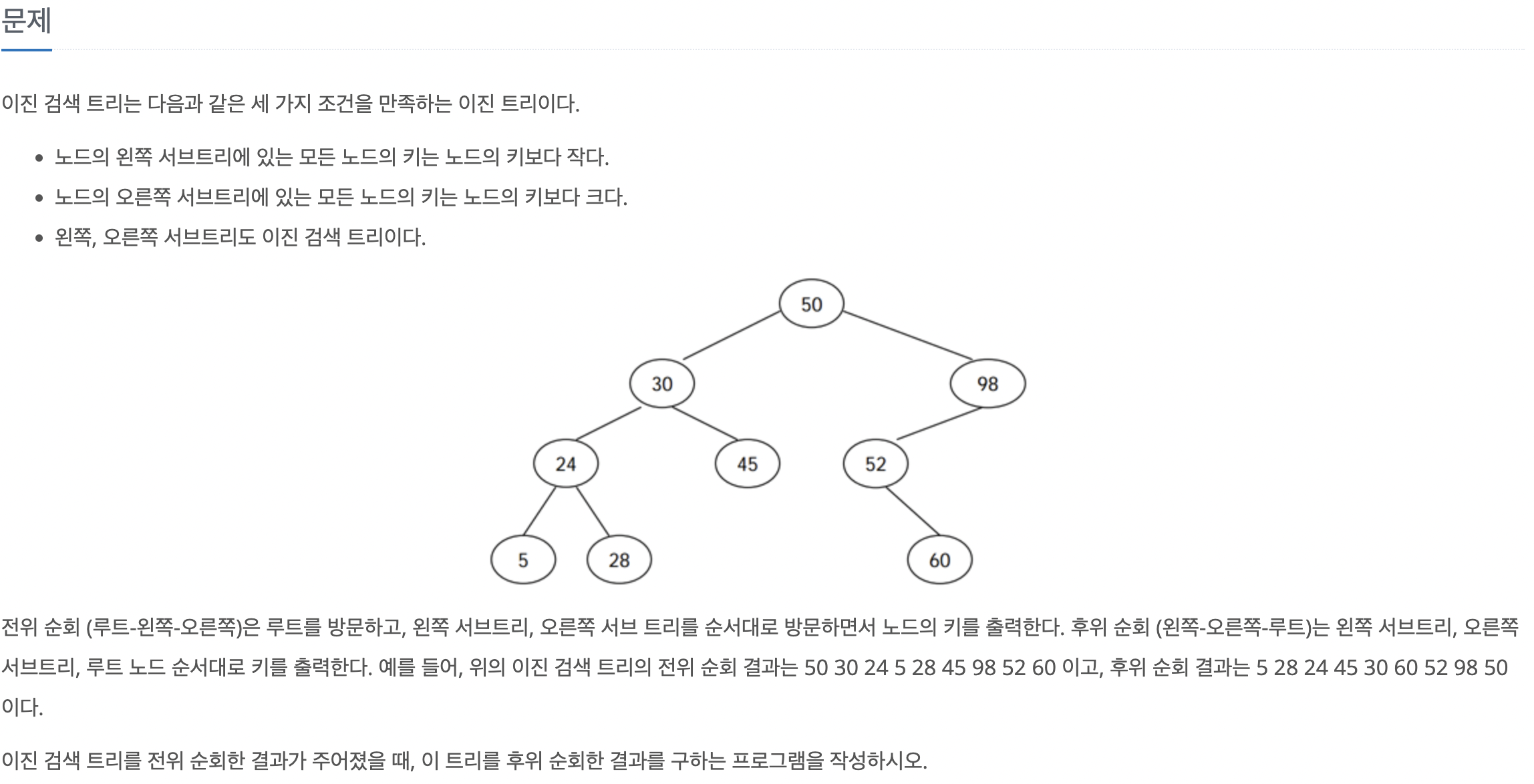
• 전위순회는 "루트-왼쪽-오른쪽" 순으로 이진 검색 트리를 순회한다.

• 이때, 이진 검색 트리에서 왼쪽은 루트보다 작은 노드들, 오른쪽은 루트보다 큰 노드들이다. 따라서, 입력 50 30 24 5 28 45 98 52 60은 아래와 같이 나누어진다.
  50 | 30 24 5 28 45 | 98 52 60

• 이를 반복적으로 수행하면 아래 그림과 같다.
  
  재귀적으로 "왼쪽처리 -> 오른쪽처리 -> root 출력" 동작을 반복하면 후위 순회한 결과를 얻어낼 수 있다.

• 이때, 처음으로 숫자가 root보다 커지는 인덱스를 알아낸다면 그 인덱스를 기준으로 왼쪽, 오른쪽을 구분할 수 있다.

def pre_to_post(start, end):
    if start > end:
        return
    
    root = preorder[start]

    # root보다 커지는 인덱스 찾기
    idx = start
    while idx <= end:
        if preorder[idx] > root:
            break
        idx += 1
    
    # 왼쪽
    pre_to_post(start+1, idx-1)
    # 오른쪽
    pre_to_post(idx, end)
    # 루트
    print(root)

시간초과 코드

import sys
input = sys.stdin.readline
sys.setrecursionlimit(10**9)

def pre_to_post(preorder):
    global postorder
    if len(preorder) == 0:
        return

    root = preorder[0]

    left = []
    right = []

    for i in range(1, len(preorder)):
        if preorder[i] < root:
            left.append(preorder[i])
        else:
            right.append(preorder[i])
    pre_to_post(left)
    pre_to_post(right)
    postorder.append(root)



postorder = []
preorder = []
while True:
    try:
        preorder.append(int(input()))
    except:
        break

pre_to_post(preorder)
for x in postorder:
    print(x)

• 위 코드는 맨 처음 시도한 코드인데, 시간초과가 났다.
• 통과한 코드와의 차이점은 pre_to_post함수의 내부 구현이다.
• 통과한 코드에서는 오른쪽 파트의 시작 인덱스를 찾고 break를 해준 반면,
  통과하지 못한 위 코드에서는 root를 제외한 모든 원소들을 순회하며 left, right라는 리스트를 각각 만들어 원소를 넣어줬기 때문에 시간이 소요된 것으로 보인다.