정렬(Sorting) - 2

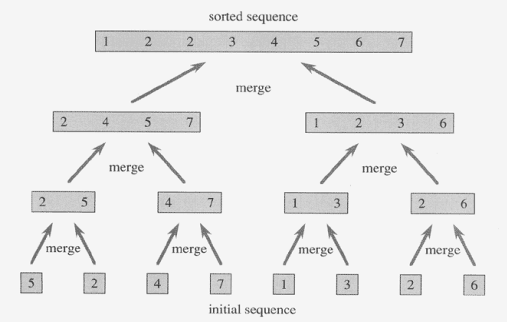
병합정렬

배열의 앞부분과 뒷부분의 두 그룹으로 나누어 각각 정렬한 후 병합하는 작업을 반복하는 알고리즘

#정렬을 마친 두 배열을 병합하는 코드
def merge_sorted_list(a: Sequence, b: Sequence, c: MutableSequence) -> None:
    """정렬을 마친 배열 a와 b를 병합하여 c에 저장"""
    pa, pb, pc = 0, 0, 0                 # 각 배열의 커서
    na, nb, nc = len(a), len(b), len(c)  # 각 배열의 원소수 

    while pa < na and pb < nb:  # pa와 pb를 비교하여 작은 값을 pc에 저장
        if a[pa] <= b[pb]:
            c[pc] = a[pa]
            pa += 1
        else:
            c[pc] = b[pb]
            pb += 1
        pc += 1

    while pa < na:              # a에 남은 원소를 복사
        c[pc] = a[pa]
        pa += 1
        pc += 1

    while pb < nb:              # b에 남은 원소를 복사
        c[pc] = b[pb]
        pb += 1
        pc += 1
        
        
        
        
#파이썬의 sorted method도 사용 가능
c = list(sorted(a + b))
    
    
import heapq
c = list(heapq.merge(a,b)) # 배열 a,b 를 병합하여 c에 저장

정렬을 마친 배열의 병합을 응용하여 분할 정복법에 따라 정렬

배열의 원소 수가 2개 이상인 경우

• 배열의 앞부분을 병합 정렬
• 배열의 뒷부분을 병합 정렬
• 배열으 앞부분과 뒷부분을 병합

def merge_sort(a: MutableSequence) -> None:
    """병합 정렬"""

    def _merge_sort(a: MutableSequence, left: int, right: int) -> None:
        """a[left] ~ a[right]를 재귀적으로 병합 정렬"""
        if left < right:
            center = (left + right) // 2

            _merge_sort(a, left, center)            # 배열 앞부분을 병합 정렬
            _merge_sort(a, center + 1, right)       # 배열 뒷부분을 병합 정렬

            p = j = 0
            i = k = left

            while i <= center:
                 buff[p] = a[i]
                 p += 1
                 i += 1

            while i <= right and j < p:
                 if buff[j] <= a[i]:
                     a[k] = buff[j]
                     j += 1
                 else:
                     a[k] = a[i]
                     i += 1
                 k += 1

            while j < p:
                a[k] = buff[j]
                k += 1
                j += 1

    n = len(a)
    buff = [None] * n           # 작업용 배열을 생성
    _merge_sort(a, 0, n - 1)    # 배열 전체를 병합 정렬
    del buff                    # 작업용 배열을 소멸

배열 병합의 시간복잡도는 O(n)이며, 데이터 원소 수가 n개 일때 병합 정렬의 단계는 log n 이므로 전체 시간복잡도는 O(N log N)

힙정렬

선택 정렬을 응용한 알고리즘이며, 힙의 특성을 이용하여 정렬함

힙의 특징?
부모의 값이 자식의 값보다 항상 크다(혹은 항상 작다)는 조건을 만족하는 완전 이진 트리
힙에서의 인덱스 관계
원소 a[i]에서

• 부모 : a[(i-1)//2]
• 왼쪽 자식 : a[i*2 + 1]
• 오른쪽 자식 : a[i*2 + 2]

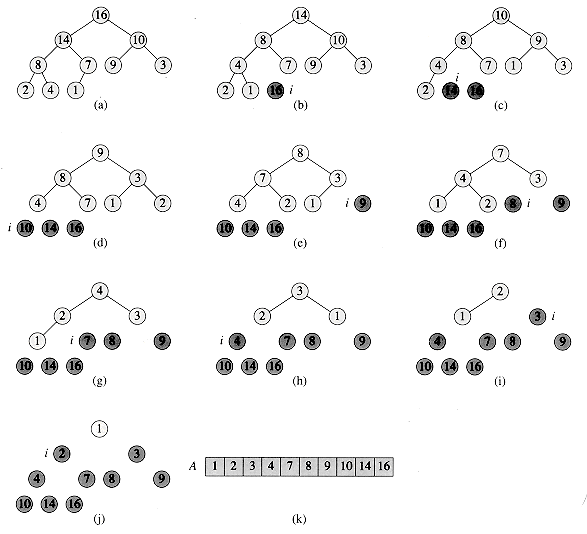
힙 정렬 메커니즘

• 힙에서 최댓값인 루트를 꺼냄
• 루트 이외의 부분을 힙으로 만듬 (가장 하단의 오른쪽에 위치한 마지막 원소를 루트로 보내고, 자신보다 값이 큰 자식과 자리를 바꾸고 아래족으로 내려가는 작업 반복, 자식의 값이 작거나 리프의 위치에 도달하면 종료)

힙 자료구조형은 배열로 구현될 수 있음

배열과 함께 고려하는 힙 정렬 메커니즘

• i 값을 n-1로 초기화
• a[0]와 a[i]를 교환
• a[0], a[1], ... , a[i-1]을 힙으로 만듬
• i값을 1씩 감소시켜 0이 되면 종료, 그렇지 않으면 2)로 돌아감

• 힙정렬에서 중요한 것은 맨처음 시작할때의 배열 역시 힙 자료구조형을 따라야 함

배열을 힙으로 만들기

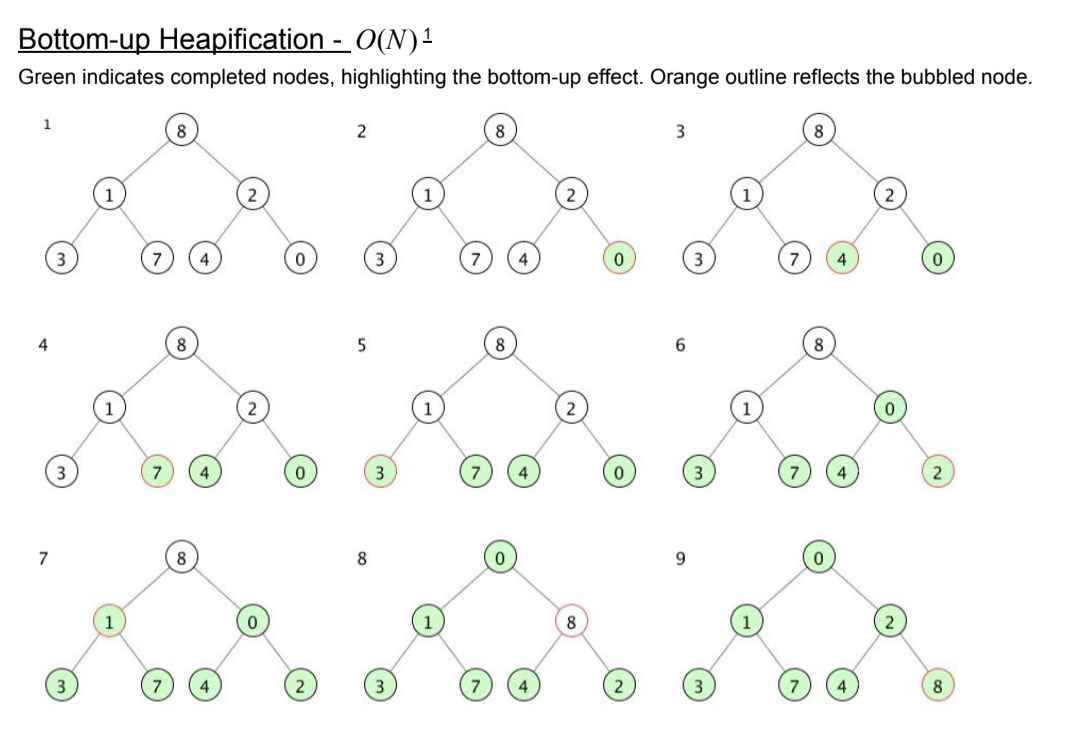
오른쪽 서브트리의 힙을 만들고, 같은 단계에 있는 왼쪽 서브트 heapify, 한단계 위로 이동하여 각각의 서브트리를 힙으로 만듬.

def heap_sort(a: MutableSequence) -> None:
    """힙 정렬"""

    def down_heap(a: MutableSequence, left: int, right: int) -> None:
        """a[left] ~ a[right]를 힙으로 만들기"""
        temp = a[left]      # 루트

        parent = left
        while parent < (right + 1) // 2:
            cl = parent * 2 + 1     # 왼쪽 자식
            cr = cl + 1             # 오른쪽 자식
            child = cr if cr <= right and a[cr] > a[cl] else cl  # 큰 값을 선택합니다.
            if temp >= a[child]:
                break
            a[parent] = a[child]
            parent = child
        a[parent] = temp

    n = len(a)

    for i in range((n - 1) // 2, -1, -1):   # a[i] ~ a[n-1]을 힙으로 만들기
        down_heap(a, i, n - 1)

    for i in range(n - 1, 0, -1):
        a[0], a[i] = a[i], a[0]     # 최댓값인 a[0]과 마지막 원소 a[i]를 교환
        down_heap(a, 0, i - 1)      # a[0] ~ a[i-1]을 힙으로 만들기

import heapq
from typing import MutableSequence

def heap_sort(a: MutableSequence) -> None:
    """힙 정렬(heapq.push와 heapq.pop를 사용)"""

    heap = []
    for i in a:
        heapq.heappush(heap, i)
    for i in range(len(a)):
        a[i] = heapq.heappop(heap)

힙정렬의 시간복잡도 O(N logN)

도수정렬(=카운팅 정렬, 계수 정렬)

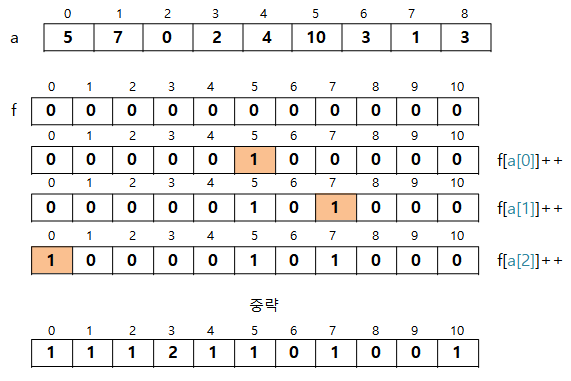
원소의 대소 관계를 판단하지 않고 빠르게 정렬하는 알고리즘 (=분포수 세기 정렬)

도수정렬 메커니즘

• 1단계 : 도수 분포표 만들기
• 2단계 : 누적 도수 분포표 f 만들기
• 3단계 : 작업용 배열 b 생성(처음에 주어진 배열과 같은 크기)
• 4단계 : 배열 복사

def fsort(a: MutableSequence, max: int) -> None:
    """도수 정렬(배열 원솟값은 0 이상 max 이하)"""
    n = len(a)           # 정렬할 배열 a
    f = [0] * (max + 1)  # 누적 도수 분포표 배열 f
    b = [0] * n          # 작업용 배열 b

    for i in range(n):              f[a[i]] += 1                     # [1단계]
    for i in range(1, max + 1):     f[i] += f[i - 1]                 # [2단계]
    for i in range(n - 1, -1, -1):  f[a[i]] -= 1; b[f[a[i]]] = a[i]  # [3단계]
    for i in range(n):              a[i] = b[i]                      # [4단계]

def counting_sort(a: MutableSequence) -> None:
    """도수 정렬"""
    fsort(a, max(a))

시간복잡도 O(n)