그래프의 기본구조
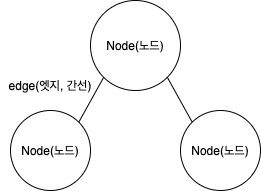
그래프는 노드(Node, Vertex)와 간선(Edge)으로 표현할 수 있음.
그래프 탐색이란 하나의 노드를 시작으로 다수의 노드를 방문하는 것을 말하며, 두 노드가 간선으로 연결되어 있다면 '두 노드는 인접하다'라고 표현함.
그래프는 크게 2가지 방식으로 표현 가능함.
- 인접행렬(Adjacency Matrix)
- 인접리스트(Adjacency List)
인접행렬
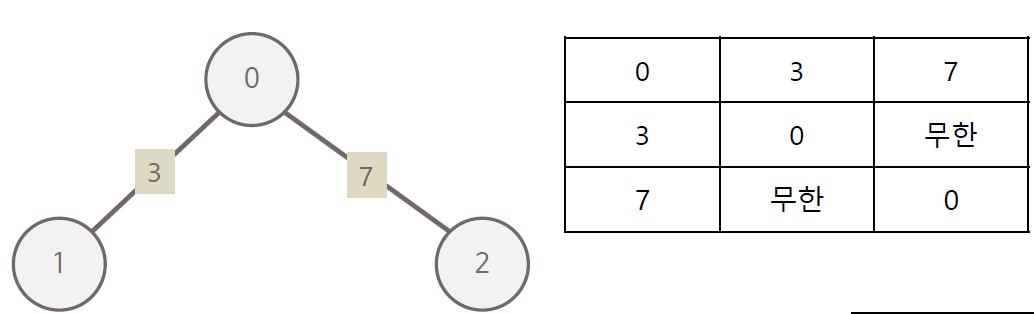
2차원 그래프로 그래프의 연결관계를 표현하는 방식
2차원 배열에 각 노드가 연결된 형태를 기록하며, 연결이 되어 있지 않은 노드끼리는 무한의 비용이라고 작성하며 실제 코드에서는 999999999,987654321 등의 값으로 초기화하는 경우가 많음
INF = 999999999 #무한의 비용 선언
# 2차원 리스트를 이용해 인접행렬 표현
graph = [
[0, 3, 7],
[3, 0, INF],
[7, INF, 0]
]
인접리스트
리스트로 그래프의 연결관계를 표현하는 방식
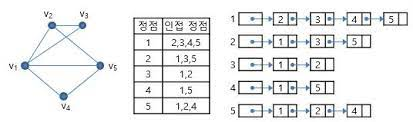
모든 노드에 연결된 노드에 대한 정보를 차례대로 연결하여 저장
인접리스트는 linked list 자료구조 이용
# 행(Row)이 3개인 2차원 리스트로 인접 리스트 표현
graph = [ []for _ in range(3)]
# 노드 0에 연결된 노드 정보 저장(노드, 거리)
graph[0].append((1, 7))
graph[0].append((2, 5))
# 노드 1에 연결된 노드 정보 저장(노드, 거리)
graph[1].append((0, 7))
# 노드 2에 연결된 노드 정보 저장(노드, 거리)
graph[2].append((0, 5))인접행렬, 인접 리스트 방식의 차이점
메모리의 관점에서 인접 행렬 방식은 모든 관계를 저장하므로 노드 개수가 많을 수록
메모리가 불필요하게 낭비되지만, 인접 리스트 방식은 연결된 정보만을 저장하기 때문에 효율적인 메모리 관리가 가능
하지만, 인접리스트 방식은 인접행렬에 비해 특정한 두 노드가 연결되어 있는지에 대한 정보를 얻는 속도가 느림
DFS
Depth-First-Search 혹은 깊이 우선 탐색
스택 자료구조를 활용한 구체적 동작 메커니즘
- 1) 탐색 시작 노드를 스택에 삽입하고 방문 처리
- 2) 스택의 최상단 노드에 방문하지 않은 인접 노트가 있으면 그 인접 노드를 스택에 넣고 방문 처리, 방문하지 않은 인접 노드가 없으면 스택에서 최상단 노드를 꺼냄
- 3) 2번의 과정을 더 이상 수행할 수 없을 때까지 반복함
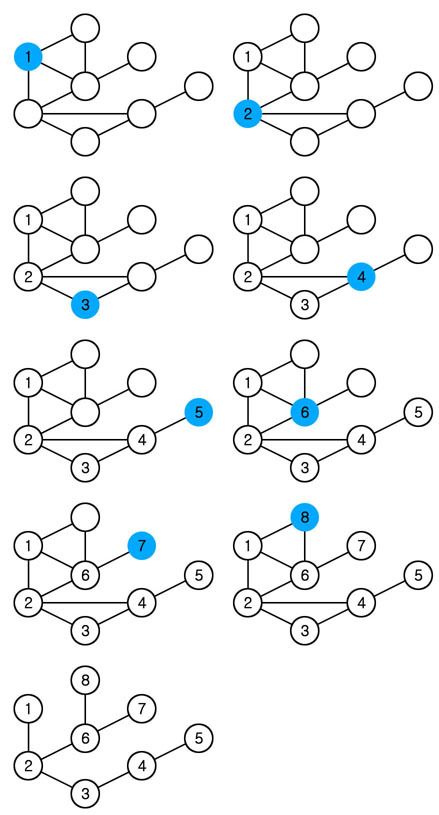
간단하게 구현이 가능하며, O(N)의 시간 소요
재귀 함수를 이용했을 때 간결하게 구현 가능함
# DFS 메서드 정의
def dfs(graph, v, visited):
#현재 노드 방문처리
visited[v] = True
print(v, end='')
# 현재 노드와 연결된 다른 노드를 재귀적으로 방문
for i in graph[v]:
if not visited[i]:
dfs(grapgh, i , visited)
BFS
Breadth-First-Search, 즉 너비 우선 탐색 알고리즘 (=가까운 노드부터 탐색함)
최대한 멀리 있는 노드를 우선적으로 탐색하는 DFS와 달리, BFS는 큐 자료구조를 이용해 가까운 노트부터 탐색함. 인접한 노드를 반복적으로 큐에 넣도록 알고리즘을 작성하면 가까운 노드부터 탐색이 가능함
큐 자료구조를 활용한 구체적 동작 메커니즘
- 1) 탐색 시작 노드를 큐에 삽입하고 방문 처리
- 2) 큐에서 노드를 꺼내 해당 노드의 인접 노드 중에서 방문하지 않은 노드를 모두 큐에 삽입하고 방문 처리
- 3) 2번의 과정을 더 이상 수행할 수 없을 때까지 반복함
# Deque 라이브러리를 활용한 BFS 구현
from from collections improt deque
def bfs(graph, start, visited) :
queue = deque([start])
#현재 노드 방문 처리
visited[start] = True
#큐가 빌때까지 반복
while queue:
#큐에서 하나의 원소를 뽑아 출력
v = queue.popleft()
print(v, end='')
#해당 원소와 연결된, 아직 방문하지 않은 원소들을 큐에 삽입
for i in graph[v]:
if not visited[i]:
queue.append(i)
visited[i] = True