이 두문제는 같은코드를 공유하기 때문에 같이 포스팅하려고 한다.
(11438에서 제출할때는 pypy3로 제출해야 제출이 된다.)
전체코드 : (출처 : 최소 공통 조상 알고리즘 10분 정복)
import sys
I = sys.stdin.readline
sys.setrecursionlimit(10**5)
LOG = 21
n=int(I())
parent,d,c = [[0 for _ in range(LOG)] for _ in range(n+1)],[0 for _ in range(n+1)],[0 for _ in range(n+1)]
graph = [[] for _ in range(n+1)]
for _ in range(n-1):
a,b=map(int,I().split())
graph[a].append(b)
graph[b].append(a)
def dfs(x,depth):
c[x],d[x] = True,depth
for y in graph[x]:
if c[y] : continue
parent[y][0] = x
dfs(y,depth+1)
def set_parent():
dfs(1,0)
for i in range(1,LOG):
for j in range(1,n+1):
parent[j][i] = parent[parent[j][i-1]][i-1]
def lca(a,b):
if d[a] > d[b] : a,b=b,a
for i in range(LOG-1,-1,-1):
if d[b] - d[a] >= (1<<i): b=parent[b][i]
if a==b : return a
for i in range(LOG - 1,-1,-1):
if parent[a][i] != parent[b][i]: a,b=parent[a][i],parent[b][i]
return parent[a][0]
set_parent()
for i in range(int(I())): print(lca(*map(int,I().split())))사용된 리스트
graph : 연결된 노드의 관계를 입력받아서 저장하는 리스트이다.
부모 관계가 주어지지 않았기 때문에 아직은 양방향임을 표현하기 위해 append를 서로 해주고 있다.
parent : parent[나][n] = 나 의 2^n번째 부모를 의미한다.
dfs함수 안에서 루트노드인 1을 기준으로 시작하기 때문에 부모관계가 문제에서 주어지진 않았지만 명확하게 알 수 있다.
c : 이 노드를 방문했었는지 체크하기 위한 리스트이다.
굳이 없애고 싶다면 d를 -1로 초기화 해서 '만약 d가 -1이면 방문하지않았다' 이런식으로 할 수도 있을것이다.
d : 이 노드의 깊이를 나타내는 리스트이다.
루트노드는 0이고 그 밑부터 하나씩 증가한다.
사용된 메소드
set_parent : dfs를 호출하여 parent리스트의 초기값을 만들어 주고, 그 이후의 parent리스트를 채우는 메소드이다.
dfs : 루트노드를 기준으로 시작하여 dfs 알고리즘의 방식으로 트리를 탐색하면서, c,d,parent 리스트를 작성한다.
lca :
if d[a] > d[b] : a,b=b,a 는 두 노드 중 깊이가 더 작은 노드를 a로 놓는다는 뜻이다.
1<<i는 2^i와 똑같은 의미이다.
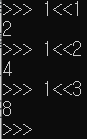
그러므로
for i in range(LOG-1,-1,-1):
if d[b] - d[a] >= (1<<i): b=parent[b][i] 이 부분의 의미는 지수만큼 a,b의 간격을 줄이는 것을 의미한다.
예를 들어 d[b]-d[a]의 거리가 11 이라면,
i==3일때 b를 2^3번째 부모로,
i==1일때 b를 2^1번째 부모로,
...
이런식으로 깊이의 차이를 11 -> 3 -> 1 -> 0 순으로 줄여준다.
이후 if a==b : return a 를 만족한다면 둘이 같은 노드를 가리키고 있으므로 리턴해주고, 아니라면 깊이는 같지만 아직 공통조상에서 못만난 상태이므로
for i in range(LOG - 1,-1,-1):
if parent[a][i] != parent[b][i]: a,b=parent[a][i],parent[b][i]를 통하여 만날때까지 부모로 a,b둘다 이동시켜준다.
