알고리즘
1.[파이썬] Trie(트라이) 자료구조

백준에서 이 문제를 풀면서 알게 된 자료구조이다.(그림 출처 : 위키백과)트라이는 탐색 트리의 종류 중 하나인데, 그림처럼 자신을 하나 하나 때서 노드에 저장하고 맨마지막 노드까지 확인하면 비로소 어떤것인지 확인 할 수 있다.이런 성질때문에 주로 알고리즘 문제를 풀때
2.[프로그래머스][파이썬]위클리 챌린지 8주차 최소직사각형
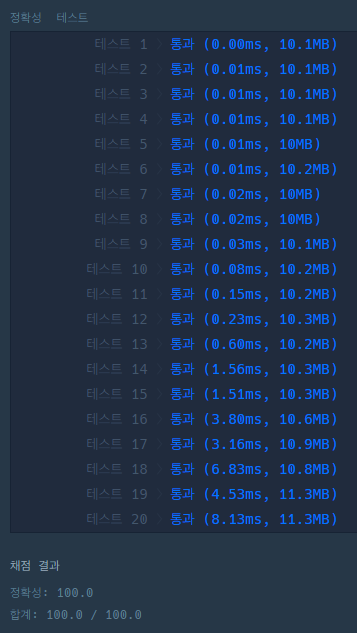
각각 가로,세로가 존재한다. 서로 위치를 바꿀 수 있으므로 결국은 가로세로중 큰놈,작은놈으로 표현할 수 있다.우리가 구해야 하는건 이 큰놈 중 가장 큰놈 \* 작은놈 중 가장 큰놈인것이다.
3.[TIL]211006(프로그래머스 위클리챌린지 9주차)

아이디어가 좋은 풀이는 아니지만 무난한 풀이가 나중에 써먹기는 좋은 것 같다. 그래프를 기록하기 위해서 defaultdict를 사용했다. defaultdict는 3번째줄 처럼 기본형태를 지정할 수 있다. 그래서 일반 딕셔너리를 사용한다면 만약 graph\[a]가 없으
4.[TIL] 211011 백준 11437_LCA,11438_LCA2
이 두문제는 같은코드를 공유하기 때문에 같이 포스팅하려고 한다.(11438에서 제출할때는 pypy3로 제출해야 제출이 된다.)전체코드 : (출처 : 최소 공통 조상 알고리즘 10분 정복)graph : 연결된 노드의 관계를 입력받아서 저장하는 리스트이다. 부모 관계가 주
5.프로그래머스 위클리 챌린지 10주차 교점에 별 만들기

이렇게 수학적인 좌표개념과 컴퓨터에서 사용하는 좌표개념이 혼용되는 문제에서는 이점만 잘 유의해주면 쉽게 접근 할 수 있다.정수판별 부분을 조금 수정한다면혹은이런식으로도 표현 할 수 있다.만약 최대,최소를 구해야되는 문제가 아니었다면 굳이 이중for문으로 탐색하기 보다는
6.프로그래머스 위클리챌린지 12주차 피로도

맨처음에는 길이 k의 리스트를 놓고 dp로 풀어보려고 했는데, 최소피로도가 까다롭게 작동해서 그래프탐색 문제를 풀때와 비슷한 느낌의 풀이를 해보았다.첫 항은 \[k,\[]]로 설정해준다. 이는 남은 채력이 k이고, 현재 \[] 를 방문했다는 뜻이다.while문안에서 d