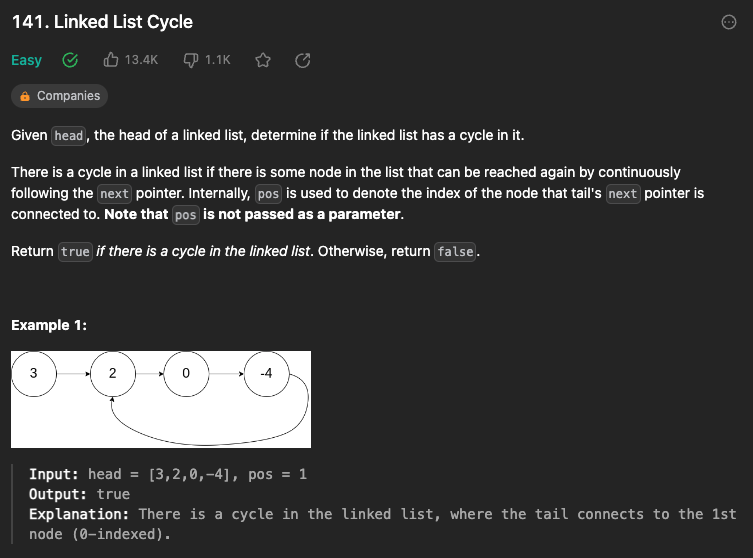
문제

// Definition for singly-linked list.
class ListNode {
    int val;
    ListNode next;
    ListNode(int x) {
        val = x;
        next = null;
    }
}

ListNode로 구현된 singly-linked list에서 사이클의 존재여부를 구하는 문제이다.

첫번째 풀이

문제를 보자마자 가장 쉽게 떠오르는 아이디어는 방문을 활용한 풀이이다. 노드를 next로 옮기면서 노드가 이미 방문한 노드이면 방문한 사이클이 존재하므로 true를 리턴한다.

방문을 확인하기위해 HashSet을 사용하였다. 방문한 노드는 HashSet에 추가하며 방문여부는 노드가 HashSet에 포함되었는지 확인한다. 노드가 HashSet에 포함되었다면 사이클이 존재하고 노드가 null이면 리스트의 끝으로 사이클이 존재하지 않는다.

이 풀이는 모든 노드를 한번씩 탐색하므로 시간복잡도 $O(n)$이며 방문여부를 체크하기위해 HashSet을 사용해 공간복잡도 또한 $O(n)$이다.

public class Solution {
    public boolean hasCycle(ListNode head) {
        Set<ListNode> visit = new HashSet<>();

        ListNode node = head;
        while (node != null && !visit.contains(node)) {
            visit.add(node);
            node = node.next;
        }

        return node == null ? false : true;
    }
}

두번째 풀이

문제에서 공간복잡도를 $O(1)$로 풀어보라고 하였다. 공간복잡도를 $O(1)$로 만드려면 방문을 체크하는 HashSet을 사용하지 않으면서 사이클의 여부를 판단해야한다.

이를 위해 LinkedList에서 사이클을 검출하는 알고리즘인 Floyd's Cycle Detection을 사용했다. 이 알고리즘은 다음과 같다.

1. slow와 fast 두 개의 포인터를 사용하며 맨 처음에는 LinkedList의 head를 가르킨다.
2. slow는 한칸 전진, fast는 두칸 전진한다.
3. fast가 null이 아니면서 slow와 같지 않을 때까지 2번 과정부터 반복한다.

slow(Tortoise)보다 fast(Hare)가 한칸씩 더 전진하기 때문에 거북이와 토끼 알고리즘이라고도 불린다.

반복이 끝났을 때 fast가 null이면 해당 LinkedList는 사이클이 존재하지 않는다. 하지만 fast와 slow가 같다면 사이클이 존재하는 것이다. LinkedList에 사이클이 존재한다면 앞서가는 fast가 사이클을 돌아 언젠가는 slow와 만나기 때문이다.

Floyd's Cycle Detection Algorithm에 대한 설명은 여기에서 참고할 수 있다.

이 알고리즘을 문제에 그대로 적용시키면 방문을 위한 HashSet을 사용하지 않고 fast, slow 두 포인터만 사용하므로 공간복잡도를 $O(1)$로 만들 수 있으며 시간복잡도는 첫번째 풀이와 마찬가지로 $O(n)$이다.

public class Solution {
    public boolean hasCycle(ListNode head) {
        ListNode slow = head;
        ListNode fast = head;
        while (fast != null && fast.next != null) {
            slow = slow.next;
            fast = fast.next.next;

            if (slow == fast) {
                return true;
            }
        }

        return false;
    }
}

다른 Solution들을 살펴봐도 Floyd's Cycle Detection으로 풀이한게 가장 많았다. 선형시간, 상수의 공간복잡도를 갖기 때문에 가장 적절한 풀이라고 생각한다.