문제

바이너리 서치 트리의 루트 노드가 주어지고 이 트리에 속한 임의의 두 노드를 선택했을 때 두 노드 값의 차이가 가장 작은 것을 리턴해야한다. 위 그림의 예제에서 값이 2인 노드와 1인 노드를 선택했을 때 값이 차이가 1로 가장 작기 때문에 1을 리턴하면 된다. 또는 4와 3을 선택해도 값의 차이가 1이다.

첫번째 풀이

주어진 트리가 바이너리 서치 트리로 왼쪽 자식 노드는 부모 노드보다 작은 값이며 오른쪽 자식 노드는 부모 노드보다 큰 값이 된다. 이 특성을 활용하면 한 노드를 선택했을 때 가장 차이가 적은 결과를 얻기 위해 선택해야할 노드가 정해진다.

가장 차이가 적은 두 노드를 선택하려면 해당 노드와 $x$축으로 가장 가까운 노드를 선택하면 된다.

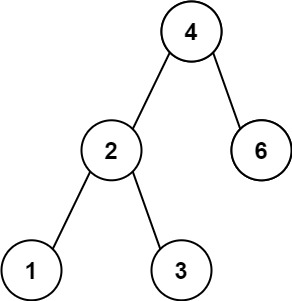
예를 들어 위와 같은 바이너리 서치 트리가 주어졌을 때 높이와 상관없이 왼쪽부터 $x$ 축으로 변환하면 다음과 같다.

node:	1 2 3 4 6
x:		1 2 3 4 5

루트 노드인 4의 $x$축 값은 4이며 이와 가장 가까운 3 노드($x$ = 3)인 노드와 차이가 가장 적다. 또한 $x = 2$인 2 노드와 가장 가까운 $x=1$인 1 노드와 차이가 가장 적다.

즉 부모 노드를 기준으로 부모 노드보다 작은 값 중의 가장 큰 값(왼쪽 자식들 중 가장 큰 노드)와 큰 값 중의 가장 작은 값(오른쪽 자식들 중 가장 작은 노드)의 차이가 항상 최소가 된다.

따라서 첫번째 풀이는 모든 부모 노드를 조회하며 왼쪽 자식들 중 가장 큰 노드와 오른쪽 자식들 중 가장 작은 노드와의 차이를 계산해 그 중 최솟값을 구하도록 풀이하였다.

class Solution {

    private int answer;
    public int getMinimumDifference(TreeNode root) {
        Queue<TreeNode> queue = new ArrayDeque<>();
        queue.add(root);

        int minimumDiff = Integer.MAX_VALUE;
        while (!queue.isEmpty()) {
            TreeNode node = queue.poll();

            if (node.left != null) {
                queue.add(node.left);
                minimumDiff = Math.min(minimumDiff, node.val - getMaxAtLeftSide(node.left));
            }

            if (node.right != null) {
                queue.add(node.right);
                minimumDiff = Math.min(minimumDiff, getMinimumAtRightSide(node.right) - node.val);
            }
        }

        return minimumDiff;
    }

    private int getMaxAtLeftSide(TreeNode node) {
        if (node.right == null) {
            return node.val;
        }

        return getMaxAtLeftSide(node.right);
    }

    private int getMinimumAtRightSide(TreeNode node) {
        if (node.left == null) {
            return node.val;
        }

        return getMinimumAtRightSide(node.left);
    }
}

시간복잡도는 모든 노드를 조회($O(n)$)하며 한 노드를 선택했을 때는 노드를 거치며 조회하는 노드가 반씩 줄어들어($O(logn)$)으로 전체 시간복잡도는 $O(nlogn)$이 된다. 공간복잡도는 $O(n)$이다.

두번째 풀이

첫번째 풀이에서 코드만 봐도 모든 부모 노드에서 왼쪽 자식 중 가장 큰 노드, 오른쪽 자식 중에 가장 작은 노드를 구하는 재귀함수를 실행하므로 효율이 좋지 않다. 실제로 결과도 하위 25%에 속하는 안좋은 성능으로 나왔다.

이를 개선하기 위해서 한 번의 재귀로 풀이해야 한다는 것은 감을 잡았지만 결국 구현을 하지 못해 Solution을 참고하고 풀었다. Soluion들의 풀이는 중위순회(inorder traversal)를 활용해 풀이하였다. 코드는 다음과 같다.

class Solution {

    private int answer = Integer.MAX_VALUE;
    private TreeNode prev;

    public int getMinimumDifference(TreeNode root) {
        inorder(root);
        return answer;
    }

    private void inorder(TreeNode node) {
        if (node == null) {
            return;
        }

        inorder(node.left);

        if (prev != null) {
            answer = Math.min(answer, node.val - prev.val);
        }
        prev = node;

        inorder(node.right);
    }
}

나는 이 풀이의 핵심은 prev라고 생각한다. 중위 순회의 규칙에 맞게 업데이트하면 부모 노드를 기준으로 왼쪽으로 순회한 결과로 prev는 왼쪽 자식들 중 가장 큰 노드를 가리키고 있게 된다. 오른쪽으로 순회할 경우에는 부모 노드를 가리키고 있기 때문에 순회 과정에서 오른쪽 자식 중 가장 작은 노드와 부모 노드의 차이를 구할 수 있게 된다.

즉 이 과정은 모든 부모 노드에서 왼쪽 자식들 중 가장 큰 노드와 오른쪽 자식들 중 가장 작은 노드와 차이를 구하는 것이다.

모든 노드를 탐색하기 때문에 시간복잡도는 $O(n)$이며 노드 수만큼 스택에 함수가 쌓이기 때문에 공간복잡도 또한 $O(n)$이된다. 시간복잡도가 감소한 만큼 실행시간도 2ms → 0ms로 줄일 수 있게 되었다.

첫번째 문제 풀이 후 개선하는 과정에서 재귀함수 구현을 생각할 때 왼쪽 자식과 오른쪽 자식 모두 탐색해 왼쪽 자식 중 가장 큰 노드, 오른쪽 자식 중 가장 작은 노드를 찾는 방법을 생각해내지 못했다. 하지만 Solution은 Inorder traversal이며 나 또한 잘 알고있는 것이었다. 복습하고 많은 문제를 풀어보면서 이미 알고 있는 것들을 어떻게 응용할 수 있는지 고민하며 응용력을 높여야겠다.