문제

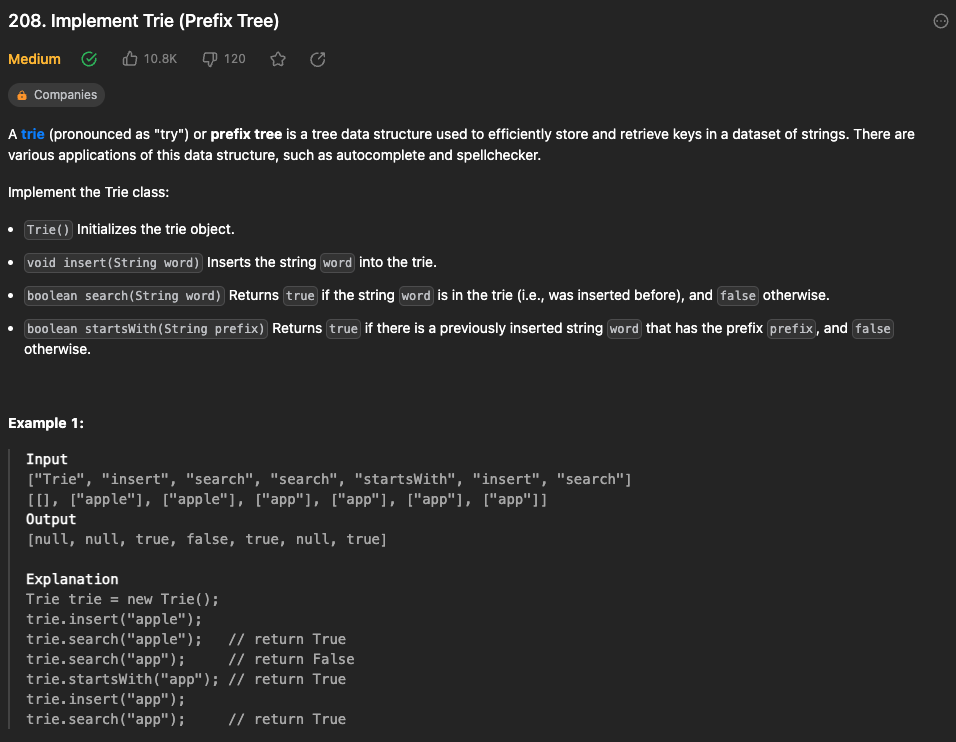
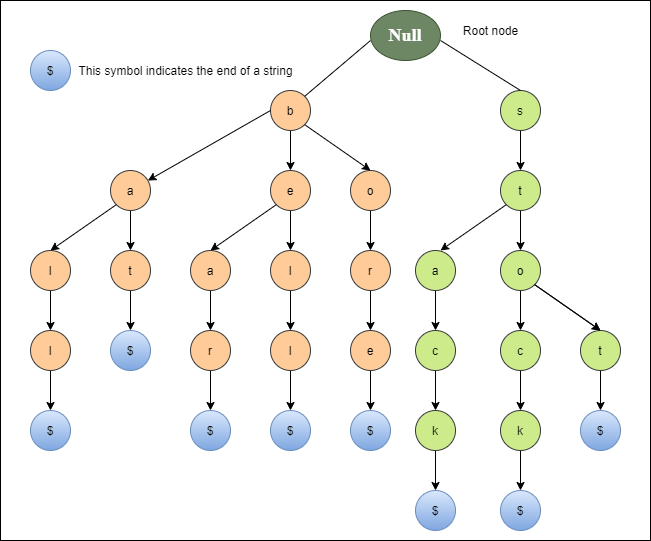
Trie 자료구조의 삽입, 검색, 접두가 검색 함수를 구현하는 문제이다. Trie는 트리(Tree)의 일종으로 문자열을 효과적으로 저장하고 검색하기 위한 자료구조이다. 접두가 검색, 자동 완성, 사전 검색 등에 주로 사용된다.

풀이

위 3가지 함수의 구현은 대체로 비슷하다. 각 함수의 의사코드는 다음과 같다.

삽입

Node current = root // 루트 노드부터 시작한다.
for(char ch : String input) // 삽입하려는 문자열의 문자를 반복한다.
	Node child = current.getChild(ch) // 현재 노드에서 삽입할 문자의 노드를 찾는다.
    if (child == null) // 삽입할 문자의 노드가 없다면
    	child = new Node() // 삽입할 문자의 노드를 만들고
        current.addChild(child) // 현재 노드에 추가한다.
    current = child // 현재 노드를 자식 노드로 변경한다.

검색

Node current = root // 루트 노드부터 시작한다.
for(char ch : String input) // 검색하려는 문자열의 문자를 반복한다.
	Node child = current.getChild(ch) // 현재 노드에서 검색할 다음 문자의 노드를 찾는다.
    if (child == null) // 검색할 다음 문자의 노드가 없다면
    	return false // 해당 문자열은 존재하지 않는다.
   	current = child // 존재하면 현재 노드를 자식 노드로 변경한다.
return current.isEndOfWord() // 문자열이 존재하더라도 단어의 끝 노드가 아니라면 존재하지 않는 것이다.

접두사 검색

Node current = root // 루트 노드부터 시작한다.
for(char ch : String prefix) // 검색하려는 문자열의 문자를 반복한다.
	Node child = current.getChild(ch) // 현재 노드에서 검색할 다음 문자의 노드를 찾는다.
    if (child == null) // 검색할 다음 문자의 노드가 없다면
    	return false // 해당 문자열은 존재하지 않는다.
   	current = child // 존재하면 현재 노드를 자식 노드로 변경한다.
return ture // prefix로 시작하는 문자열이 존재한다.

이 3가지 함수의 구현은 반복문으로도 가능하고 재귀로도 구현가능하다. 첫번째 풀이에서는 두 방법을 모두 사용해보려고 삽입만 재귀로 구현하고 검색, 접두사 검색은 반복문으로 풀이했다.

class Trie {

    private Node root;

    public Trie() {
        this.root = new Node();
    }
    
    public void insert(String word) {
        insert(this.root, word, 0);
    }

    private void insert(Node current, String word, int idx) {
        if (idx == word.length()) {
            current.endOfWord();
            return;
        }

        char ch = word.charAt(idx);
        Node child = current.getChild(ch);
        if (child == null) {
            current.addChild(ch);
        }

        insert(current.getChild(ch), word, idx + 1);
    }
    
    public boolean search(String word) {
        int len = word.length();
        Node current = this.root;
        for (int i = 0; i < len; i++) {
            Node child = current.getChild(word.charAt(i));
            if (child == null) {
                return false;
            }

            current = child;
        }

        return current.isEndOfWord();
    }
    
    public boolean startsWith(String prefix) {
        int len = prefix.length();
        Node current = this.root;
        for (int i = 0; i < len; i++) {
            Node child = current.getChild(prefix.charAt(i));
            if (child == null) {
                return false;
            }

            current = child;
        }

        return true;
    }

    public static class Node {

        private Map<Character, Node> child = new HashMap<>();
        private boolean isEndOfWord;

        public void addChild(Character ch) {
            this.child.put(ch, new Node());
        }

        public Node getChild(Character ch) {
            return child.get(ch);
        }

        public void endOfWord() {
            this.isEndOfWord = true;
        }

        public boolean isEndOfWord() {
            return this.isEndOfWord;
        }

        public boolean hasChild() {
            return !child.isEmpty();
        }
    }
}

두번째 풀이

첫번째 풀이에서 Node 클래스의 child를 Map으로 풀이했다. 하지만 이 문제에서 문자들은 소문자 알파벳으로 한정되어있어 길이가 26인 char형 배열로 개선할 수 있으며 메모리의 접근은 배열이 가장 빠르기 때문에 성능에 도움이 될 것으로 생각하였다.

class Trie {

    private Node root;

    public Trie() {
        this.root = new Node();
    }
    
    public void insert(String word) {
        insert(this.root, word, 0);
    }

    private void insert(Node current, String word, int idx) {
        if (idx == word.length()) {
            current.endOfWord();
            return;
        }

        char ch = word.charAt(idx);
        Node child = current.getChild(ch);
        if (child == null) {
            child = new Node();
            current.addChild(ch, child);
        }

        insert(child, word, idx + 1);
    }
    
    public boolean search(String word) {
        int len = word.length();
        Node current = this.root;
        for (int i = 0; i < len; i++) {
            Node child = current.getChild(word.charAt(i));
            if (child == null) {
                return false;
            }

            current = child;
        }

        return current.isEndOfWord();
    }
    
    public boolean startsWith(String prefix) {
        int len = prefix.length();
        Node current = this.root;
        for (int i = 0; i < len; i++) {
            Node child = current.getChild(prefix.charAt(i));
            if (child == null) {
                return false;
            }

            current = child;
        }

        return true;
    }

    private class Node {

        private Node[] child = new Node[26];
        private boolean isEndOfWord;

        public void addChild(char key, Node child) {
            this.child[key - 'a'] = child;
        }

        public Node getChild(char key) {
            return this.child[key - 'a'];
        }

        public void endOfWord() {
            this.isEndOfWord = true;
        }

        public boolean isEndOfWord() {
            return this.isEndOfWord;
        }
    }
}

이 결과 37ms → 30ms로 실행속도를 줄일 수 있었다.

개선하기 위한 시도..

두번째 풀이의 실행속도는 좋은 편에 속한다. 하지만 삽입 함수를 재귀로 구현했지만 반복문으로도 구현할 수 있고 일반적으로 재귀보다 반복문이 실행속도가 빠르기 때문에 반복문으로 수정해 개선하려고 했다.

하지만 이상하게도 더 늦은 실행 속도가 나왔다. 그래서 혹시나하는 마음에 검색과 접두사 검색 함수도 재귀로 수정해 제출해보았다. 역시나 더 빠른 속도가 나오진 않았다. 시도했던 방법 중 가장 빠른 결과를 얻을 수 있었던 방법은 삽입만 재귀로 구현하고 나머지 두 함수는 반복문으로 구현하는 것이 가장 빨랐다. 원인을 찾으려고 노력했으나 이유를 발견하지 못했다..