링크 에서 가져왔습니다.
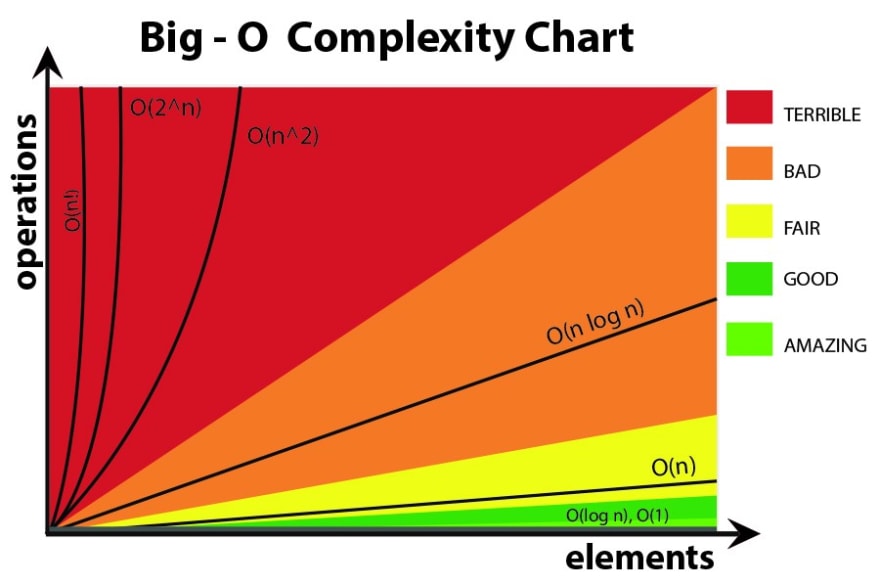
"내 주식이 O(n!) 으로 오른다면..."
주식 차트가 O(n!) 라면 떡상도 이런 떡상이 없겠지만 알고리즘은 반대입니다. 위의 그래프가 직관적으로 보여주는 것처럼 좋은 알고리즘은 낮은 시간 복잡도를 지니게 마련이죠.
구글에서 시간 복잡도를 검색하면 위키백과의 시간복잡도 자료가 가장 먼저 검색됩니다. 문제는 검색은 되는데 도저히 읽을 엄두가 안 난다는 것이죠.
이런 상황에서 우리는 코드스테이츠 크루분이 알려주신 철학을 고민해 볼 수 있습니다. 바로 나에게 필요하고 소화 가능한 부분만 골라서 편식하는 공부방법인데요. 공식문서나 stackoverflow 를 포함한 거의 모든 자료는 보통 바로 소화해내기 어려운 자료이기 때문에, 그 중에서 지금 내가 당장 필요하고 또 이해가 가능한 부분만 먼저 가져오는 겁니다.
상단의 위키백과에서 하나 가져오겠습니다.
시간 복잡도는 문제를 해결하는데 걸리는 시간과 입력의 함수 관계
이해되는 부분일 것 같은데 막상 찬찬히 살펴보면 무슨 뜻인지 아리송하기도 합니다. '문제를 해결하는데 걸리는 시간'이라는 말은 알겠는데, '입력의 함수' 라는 표현이 좀 이상하죠. 이럴 때는 영어 자료를 한 번 살펴봐야 합니다.
In computer science, the time complexity is the computational complexity that describes the amount of computer time it takes to run an algorithm.
나름대로 번역해보면, "CS (Computer Science 의 줄임말) 에서 시간 복잡도란 바로 계산에 관한 복잡도인데, 컴퓨터가 알고리즘을 실행하는데 들어가는 시간의 양에 관해 설명하는 것이다." 정도일 것 같은데요. 알고리즘의 성능에 관련되어 있다는 것을 알 수 있습니다.
컴퓨터의 성능이 많이 좋아졌다고는 해도, 여전히 컴퓨터가 감당 가능한 연산 능력에는 분명 한계란 것이 존재합니다. 문제는 컴퓨터는 직관적으로 정보를 파악하지 않고, 하나하나 다 실행해보고 나서야 결과를 내놓는다는 점이죠.
게다가 컴퓨터가 감당 가능한 정도라고 해도, 연산이 오래 걸릴 수록 유저는 답답함을 느끼게 될 겁니다. 만약 한국사람이라면 더 말할 것도 없겠죠.. 따라서 알고리즘을 구현하고 프로그래밍할 때 우리는 연산 능력과 함께 시간 복잡도를 생각해봐야 합니다.
시간 복잡도를 이해할 수 있는 좋은 예제는 바로 피보나치 수열입니다. 재귀를 사용한 피보나치 함수는 그 모양이 매우 간단하죠. 하지만 함수 내부에서 자기 자신을 두 번이나 재귀호출한다는 특성 덕분에 시간복잡도가 O(2^n) 으로 기하급수적으로 증가합니다. 상단의 이미지를 보면 O(n!) 만큼은 아니더라도 Terrible 한 것은 분명해보입니다.
이 때 우리는 연산의 중복을 막기 위해 이미 연산이 끝난 것들을 따로 저장해두고, 필요한 경우 바로 호출해서 사용하는 방식으로 시간 복잡도를 획기적으로 낮출 수 있습니다. 이를 메모이제이션 (Memoization) 이라고 합니다.
본문 내 링크 외 참고자료
