해당 게시글은 LG Aimers Phase1의 수업 내용을 정리한 글로, 모든 내용의 출처는 https://www.lgaimers.ai/ 입니다.

Principle and Structure

Bayesian 원리 및 작동방식

• Outcome : P(궁금한 대상 | Data)

• 확률 : 불확실성을 전달하는 데에 가장 확실하고 효과적인 묘사 방법

• 궁금한 대상 : 모수 ~ 모수에 대한 확률을 알기 위해 베이지안 통계 활용

• 예시

  • Model : $y=\beta_0+\beta_1X+\varepsilon$

    • $\varepsilon = N(0, \sigma^2)$

  • Result : $\beta_0=? \ \beta_1=? \ \sigma^2=?$

    • $P(\beta_0|Data), P(\beta_1|Data),P(\sigma^2|Data)$

  • 무엇이 질문과 답을 끌어가는가? : parameters

    • Question = 사전확률 : $P(params)$ (Prior)

      • 데이터가 없는 상태
      • $P(\beta_0), P(\beta_1), P(\sigma^2)$ → $P(\beta), P(\sigma^2)$
      • $\beta \sim N(\beta_{prior},\sum_{prior})$, $\sigma^2 \sim IG(\mathsf{a}_{prior},\mathsf{b}_{prior})$
        • 왜 $\beta$가 정규분포를 띈다고 생각했나요? → 양수, 음수 값을 모두 가질 수 있으며 그 확신의 정도를 나타낼 수 있는 분포가 정규분표이기 때문
        • 왜 $\sigma^2$가 역감마분포를 띈다고 생각했나요? → 분산에 대한 파라미터이기에 음수를 가질 수 없다고 판단했고 양수의 값을 갖는 분포 중 적절한 것이 역감마분포라고 판단

    • 우도 : $P(Data|params)$ (Likelihood)

      • $P(y|\beta_0, \beta_1, \sigma^2,X)$ → $P(y|\beta,\sigma^2,X)$
      • $y \sim N(X\beta,\sigma^2I)$ ← $y=\beta X+\varepsilon \ \ [\varepsilon\sim N(0, \sigma^2I)]$

    • Result = 사후확률 : $P(params|Data)$ (Posterior)

      • 알고자 하는 결과물
      • $P(\beta_0|y,X), P(\beta_1|y,X), P(\sigma^2|y,X)$ → $P(\beta|y,X), P(\sigma^2|y,X)$
      • $\beta \sim N(\beta_{post},\sum_{post})$,$\sigma^2 \sim IG(\mathsf{a}_{post},\mathsf{b}_{post})$
        • 실제 데이터를 관찰한 뒤 파라미터 분포를 명확히 할 수 있음

    • Bayesian Framework

      • 파라미터에 대한 사전 믿음, 확신이 강하다면, 사전확률의 분산 값이 작게 형성됨 ~ 추후 사후확률 구하는 식에서 사전확률에서 정한 파라미터의 평균이 큰 영향력을 가지게 됨 = 데이터의 영향력이 작아지게 됨
      • 파라미터에 대한 사전 믿음, 확신이 약하다면, 사전확률의 분산 값이 크게 형성됨 ~ 추후 사후확률 구하는 식에서 사전확률에서 정한 파라미터의 평균이 작은 영향력을 가지게 됨 = 데이터의 영향력이 커지게 됨
      • $Posterior \propto Prior \times Likelihood$

    • 왜 Bayesian인가

      • $Posterior Probability=\frac{Prior Probability\times Likelihood}{Marginalized Probability}$

      • $\Longleftrightarrow P(\beta|Data)=\frac{P(\beta)\cdot P(Data|\beta)}{P(Data)}$ (Bayes 정리)

        → 우리가 구하는 모든 probability outcome이 베이즈 정리를 따르기 때문에 베이지안 통계라고 일컫음

        $=\frac{P(\beta)\cdot P(Data|\beta)}{\int P(\beta)\cdot P(Data|\beta)d\beta}$ (적분) : joint probability에 대한 적분 필요 ~ 계산 복잡

      • 적분을 다루기 위한 다른 방법들

        $\Longleftrightarrow P(\beta|Data) \propto P(\beta)\times P(Data|\beta)$

        : 분모의 적분값을 일정한 상수값으로 가정하면 근사 가능

        $\Longleftrightarrow$ 몬테카를로 시뮬레이션

        : 실제 데이터에는 없지만 시뮬레이션을 통한 분포 파악 가능

Estimation Algorithm

0. $P(\beta|Data) \propto P(\beta)\times P(Data|\beta)$ 에서

   • prior과 posterior가 동일한 분포를 가질 때 : Conjugate Family
   • prior과 posterior가 상이한 분포를 가질 때 ~ posterior의 분포를 구하기 어려움
     • Simulation 이용하기!! - MCMC …

1. MCMC

   • Markov Chain : dependent on the last sample
   • Monte Carlo : drawing samples ‘many times’ from a probability distribution

2. Gibbs Sampler

   • GOAL : estimate joint posterior distribution of parameters

     = reaching the joint probability distribution via sampling from conditional distribution

     ~ approximating

not easy : $P(\theta_1, \theta_2|y, X)$ → joint distribution
easy : $P(\theta_1|\theta_2, y, X), P(\theta_2|\theta_1, y, X)$ → conditional distribution
매 iteration 마다 Monte Carlo Sample ~ R번 반복

파라미터 초기화 랜덤 설정 ~ 틀릴 수 있는 것으로 가정

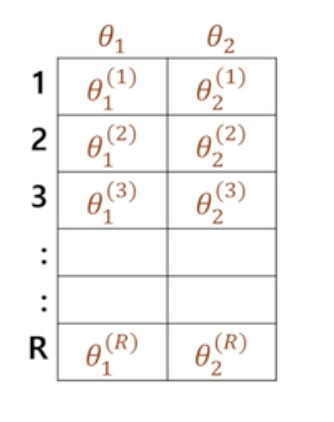
$\theta_1, \theta_2$에 대한 동시 확률 분포를 충실히 나타내는 숫자 조합
이 숫자들은 우리가 얻고자 한 joint distribution을 만족함
각 축별로 살펴보게 된다면 각 파라미터에 대한 분포를 알 수 있음

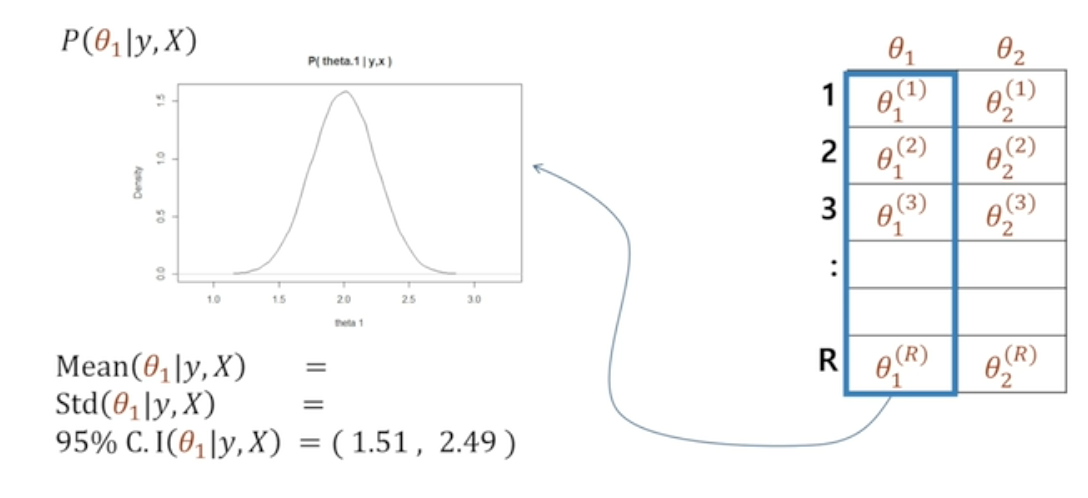
multi parameter에 대한 joint posterior distribution을 개별적인 conditional distribution을 많이 반복하여 구할 수 있게 됨
Metropolis-Hastings Algorithm
conditional posterior distribution도 모르는 경우 활용 가능한 방법

• 방법

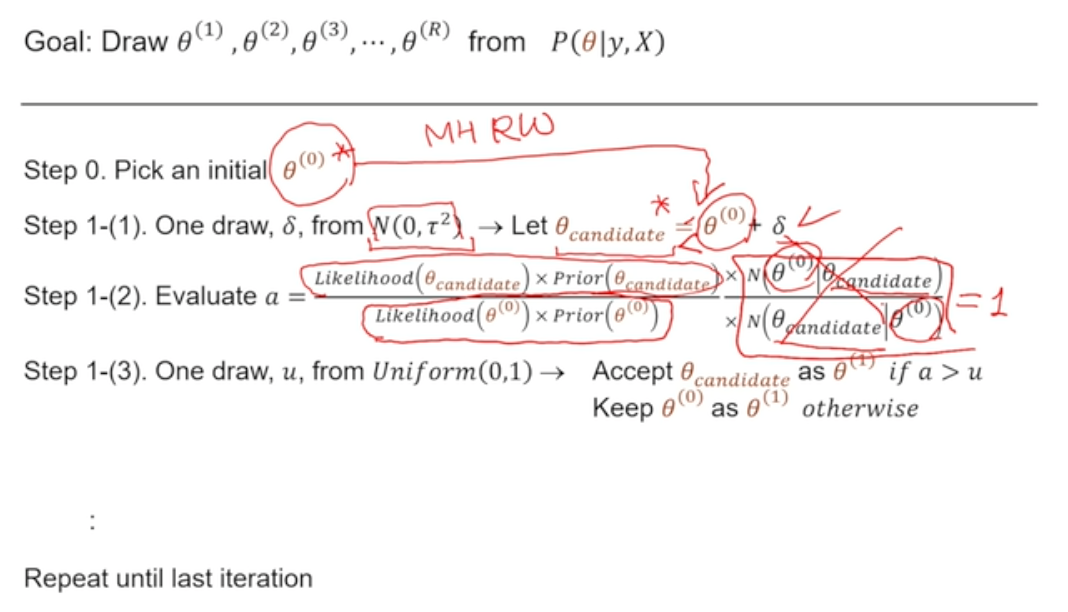
1) 매 iteration 마다 candidate draw 구하기
2) accept / reject - based on some rules that are related to the posterior distribution

• 도전자와 챔피언으로 구분하여 각각의 posterior distribution을 계산
• 도전자($\theta_{candidate})$는 챔피언($\theta)$에서 Metropolis-Hastings Random Work로 구한 값 (정규분포를 따르는 $\delta$ 더해서 구한 값)
  → step 1-(2)에서 우측의 $\frac{N(\theta|\theta_{candidate})}{N(\theta_{candidate}|\theta)} = 1$로 사라짐
• 도전자의 posterior distribution이 더 strong(확률 가능성이 더 높게)하게 나타난다면 해당 값 받아들임
  - random sampling한 $u$와 $a$값을 비교하여 $u$보다 $a$가 크면 도전자로 교체
• 그렇지 않다면, 확률적으로 새로운 도전자를 받아들일 것인지 아닌지 결정

3) accepted draw ~ used to summarize posterior distribution

• convergence가 발생하는 순간 = burn in ~ 제대로 된 posterior distribution을 찾아왔다는 것을 의미

• 실제 베이지안에 활용할 때 유의사항

  • 우리가 구하고자 하는 파라미터의 사후분포
    • 적분을 하지 않기 위해서는 우도 * 사전분포
  • 사후분포와 사전분포의 종류가 동일하지 않다면
    • 하나의 파라미터의 conditional distribution을 알 수 있다면 → gibbs sampling
      • Metropolis-Hastings에 대입하여 설명하자면 매 iteration마다 candidate draw가 accept되는 것 = all draws are ‘accepted’
    • 하나의 파라미터의 conditional distribution을 알 수 없다면 → Metropolis-Hastings
      • some draws are ‘accepted’
  • input : data, prior, likelihood, starting values
  • output : trace plot ~ 수렴 했는지 안했는지, distribution, summary statistics
  • 주의 사항
    • convergence
      • 수렴 확인하지 않으면, 실제 posterior 분포를 반영하지 않을 수 있음
    • multiple starting points
      • 다양한 시작점에서 시작해도 convergence 패턴이 동일하다면 posterior 분포가 분명하게 있다고 이야기 가능
    • burn-in
      • 특정 시점에 수렴한 뒤의 내용만 사용해야 함
    • autocorrelation - accpetance rate, ACF
      • time series와 유사한 개념
      • 매 iteration마다 얻는 draw는 이전 draw가 무슨 값이었는지에 영향을 받게 됨
        • 이 영향을 매우 크게 받게된다면, 우리가 구하고자 하는 Posterior distribution을 제대로 반영하지 못함

→ $\tau$가 매우 큰 경우 : 기존 챔피언에서 먼 곳에서 도전자 등장

• draw 분포 변동이 거의 없음 ~ 분포를 구성하기가 쉽지 않아 바람직하지 않음

→ $\tau$가 매우 작을 경우 : 기존 챔피언과 매우 가까운 곳에서 도전자 등장

• reject/accept 과정에서 새로운 도전자가 항상 accept될 것

- x축 움직임이 매우 작으나 y축 움직임 매우 활발

→ 도전자와 챔피언의 거리가 적절해야 함

• 일정 범위 내에서 안정적으로 움직임 확인 가능

이를 방지하기 위해서는 acceptance rate, ACF 확인 필요

• acceptance rate : 새로운 candidate draw를 얼마나 accept하는가
  • 이 값이 높을 경우 ACF 또한 높음 → 바람직하지 않음
  • 이 값이 낮을 경우 trace plot이 flat해짐
    → autocorrelation이 높다는 것을 의미
    → 변화가 발생하는 n구간 마다의 accepted draw만을 활용하여 건강한 plot 도출하는 것도 하나의 해결방안이 될 수 있음

Solving Real Problem

1. 특징

• prediction : 수요 예측
• heterogeneity : 개인 고객별로 parameter가 다른 상태
• conjoint method : 현재 시장 내 제품에는 없는, 새로운 feature 도입 되었을 시의 수요 예측

2. 응용

• decision problem : 누구를 타겟으로 설정할 것인가, 무엇을 제안할 것인가
• information need : 누가 가장 즉각적으로 좋아하며 반응할 것인가
• data scientist’s job : 파라미터에 대한 사후 분포 구하기

3. 베이지안 모델의 특장점

• 우측 panel data의 random effect
  • heterogeneity of beta ~ 개인의 고유한 파라미터는 전체 분포에서 random하게 추출된 것으로 볼 수 있음
• 좌측 prior distribution
  • beta의 불확실성을 보여줌
  • beta의 heterogeneity를 추정하는 데에 bayesian framework를 그대로 활용할 수 있다는 것이 베이지안 방식의 특장점
• PRIOR == HETEROGENEITY

4. 예시

• 행렬 설명
  • h : 각 고객이 갖는 상품 특징에 대한 민감도
  • z : 각 고객의 특징
• 한 개인이 i 물건을 선택했을 때, 그 원인이 $\beta_h$에 있다고 가정하면 $\beta_h$는 개인의 특징인 $z$와 기타 정보로 인해 결정된다

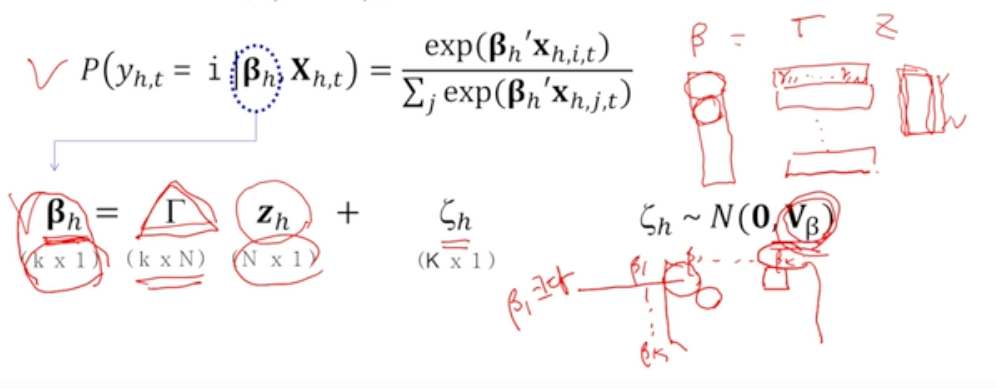
• likelihood $\frac{exp(\beta_h x_{h,i,t})}{\sum_j exp(\beta_h x_{h,j,t})}$
  • 전체 제품 중 i번째 제품이 갖는 선택 확률
  • 전체 제품이 제공하는 매력도 중 i번째 제품이 제공하는 매력도
• 다변량회귀모형
  • 한 개인이 가지고 있는 $\beta$가 $k$개의 beta coefficient를 가짐
  • 개인의 특징변수가 $N$개 있다고 가정하면 이 N개의 변수가 어떻게 beta에 영향을 미치는지 나타내는 변수가 $\gamma$
  • $V_{\beta}$ : 사람들마다 어떻게 다르며 beta들끼리의 correlation을 보여줌 ~ heterogeneity
• Model
  

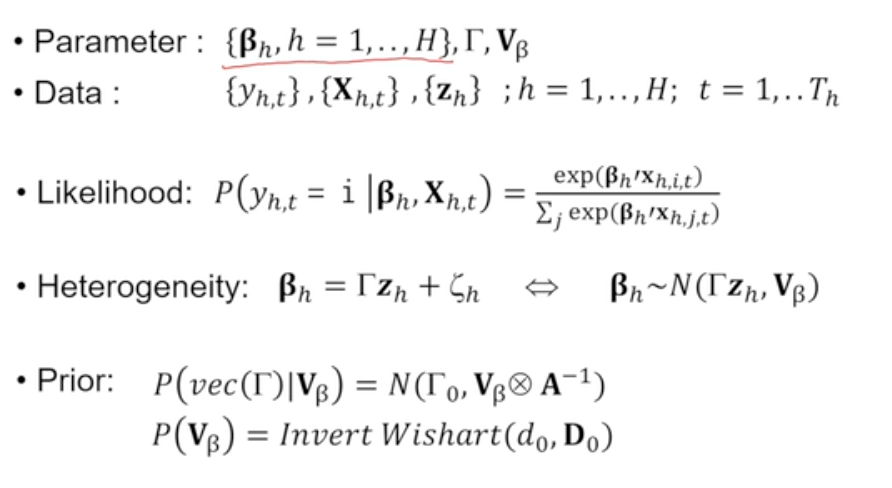
• 우리가 추정해야 하는 파라미터 : 각 개인별 beta, 개인별 beta가 개인별 특성 z와 어떤 관계를 갖는지를 나타내는 gamma, 개인별 특성이 얼마나 상이한지를 나타내는 V_beta
  • 파라미터에 대한 사후분포 추정해야 함
• 필요한 데이터 : y, X, z
• 우도 : 매 시점마다 y가 무슨 제품을 선택했는지에 대한 확률
  • log를 취해서 주로 활용함
    • 0에 가까운 값이 나올 경우 beta에 대한 계산 어렵기 때문에
    • log를 취해서 구한 beta의 값이 변하지 않기 때문에
• 사후확률 = heterogeneity : 모든 개인이 갖는 서로 다른 beta
• 사전확률 : gamma와 v_beta에 대한 분포 필요
  • gamma : normal distribution
  • v_beta : positive definity & variance-covariance matrix ~ invert wishart distribution
• 위 모델에서 beta를 구하는 과정을 각 고객별로 반복하여 Metropolis-Hastings 방식 활용

---

우도와 사후확률에 대한 관계를 이제서야 이해했다.. 통계 수업 때마다 머리에 들어오지 않아 고생했는데 이번 수업을 통해 완벽하진 않지만 갈피는 잡을 수 있어 기뻤다!