paper link
presentation link
(이 글은 위 표기한 프레젠테이션 영상을 참고하여 작성했습니다.)

Background

• attention : quadratic context bottleneck 문제 발생
  • MLP : 병렬처리
  • attention : 모든 토큰을 모든 토큰에 대해 비교

→ 연구 질문 : attention을 sub-quadratic 알고리즘으로 대체할 수 있을까?

• state space model

  • $x_i = Ax_{i-1}+Bu_i$
    $y_i = Cx_i + Du_i$

    → x = hidden state

    → u = input sentence

    → y = output sentence
    

  • $y = u*k$

    → k = kernel
    

  • 주요 특징

    • recurrent view
      • 생성에 있어 시간복잡도 O(1) (생성 속도가 input 길이에 의존하지 않음)
      • 고정된 context length 없음
    • convolutional view
      • 학습 빠름 … recurrent의 경우 vanishing gradients problem 발생 가능
    • during training
      • 시퀀스 길이 N에 대해 O(NlongN)의 공간 복잡도 가짐
      • 기존 attention은 O(N^2)의 공간 복잡도

  • 기존 transformer와의 성능 비교

    • quality에서 Perplexity 기준 꽤 큰 차이로 성능 떨어지는 것 확인 가능

      Model	PPL(OWT)
      Transformer	20.6
      S4D	24.9
      GSS	24.0

    • 효율성에 있어서 짧은 입력 받을 경우 transformer에 비해 효율성 떨어짐
      - 약 2K길이까지는 비교적 느림
      - 긴 입력에 있어서는 비교적 효율적임 (빠른 시간 내에 완료)

      → 연구 목표 : transformer와의 quality gap, efficiency gap을 없애자!

H3 : Hungry Hungry Hippo

• quality gap을 줄이기 위함

• synthetic language

  • associative recall : simple synthetic language
    $a:4\ \ b:3 \ \ c:1 \ \ a:4 \ \ a:4\ \ b:3\ \ d:2\ \ c: -> 1$
  • mimics language : recall information from earlier in the sentence
    $\textbf{Barack}\ and\ \textbf{Michelle}\ \textbf{Obama}\ went\ to\ \textbf{Harvard}\ to\ visit\ their\ \textbf{daughter}\ ->\ Malia$
    → Malia라는 다음 단어를 예측하기 위해 Barack, Michelle, Obama, Harvard, daughter 의 정보를 활용
    

• Evaluating SSMs with associative recall

  • toy data로 SSM의 associate recall 성능 비교
  • next token prediction으로 학습한 뒤, 마지막 token을 맞추는지에 대해 확인
  • 2-layer 모델로 비교

    Model	ACC
    Transformer	100.0
    S4D	38.8
    GSS	19.8

    • SSM 기반 모델은 associative recall문제를 해결하지 못함
    • Transformer는 완벽하게 해결함

• Hungry Hungry Hippos

  • Associative Recall을 위해 설계됨

    

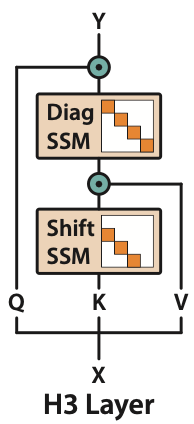
  • 설계

    • 2개의 SSM레이어 쌓기

      • Shift SSM : local lookup across sequence

        

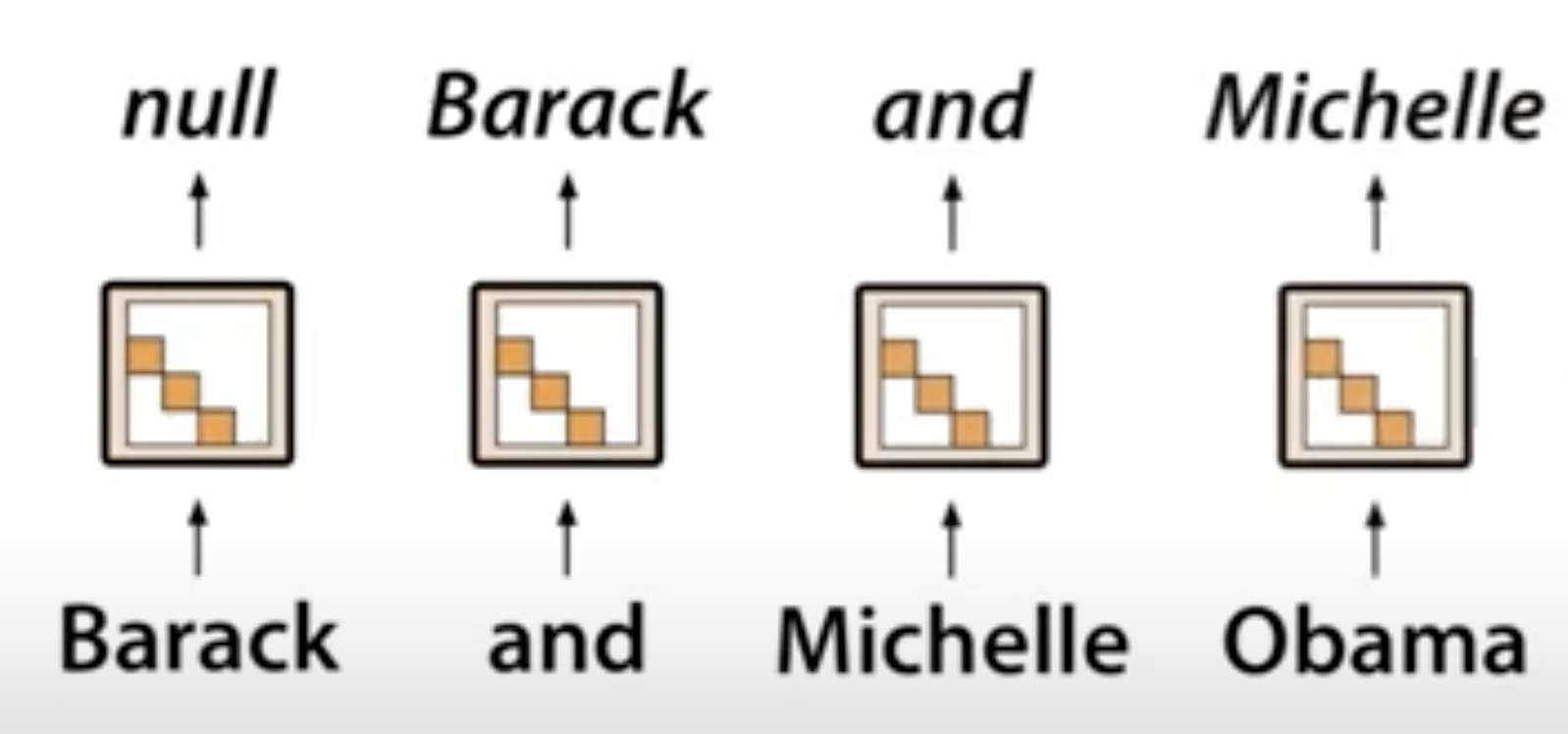
        → input에 대한 아주 짧은 local convolution으로 이해 가능
        

      • Diag SSM : global memory

        

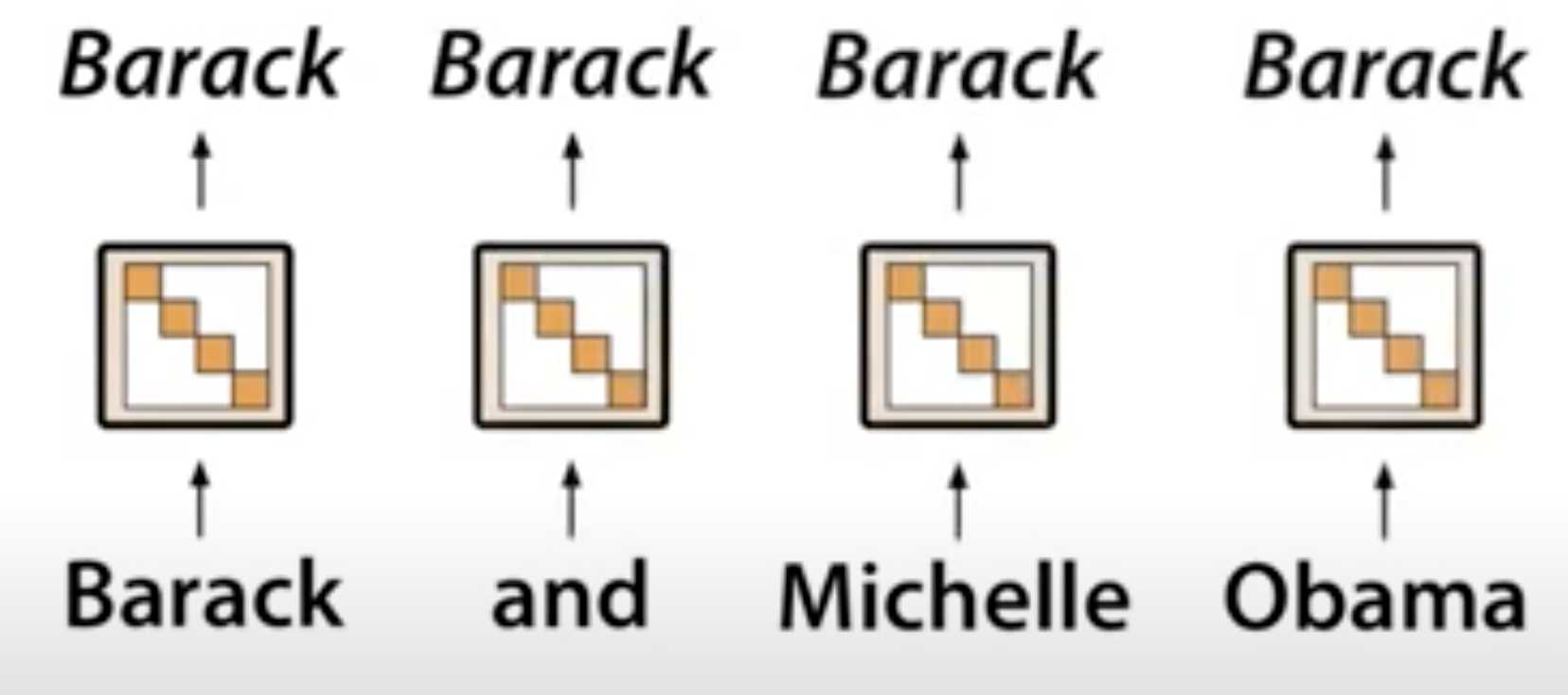
        → gating mechanism을 통해 기억할 정보를 취사선택 가능

        (기존에 알고있던 Masking과 유사한 기능인 듯..)

        

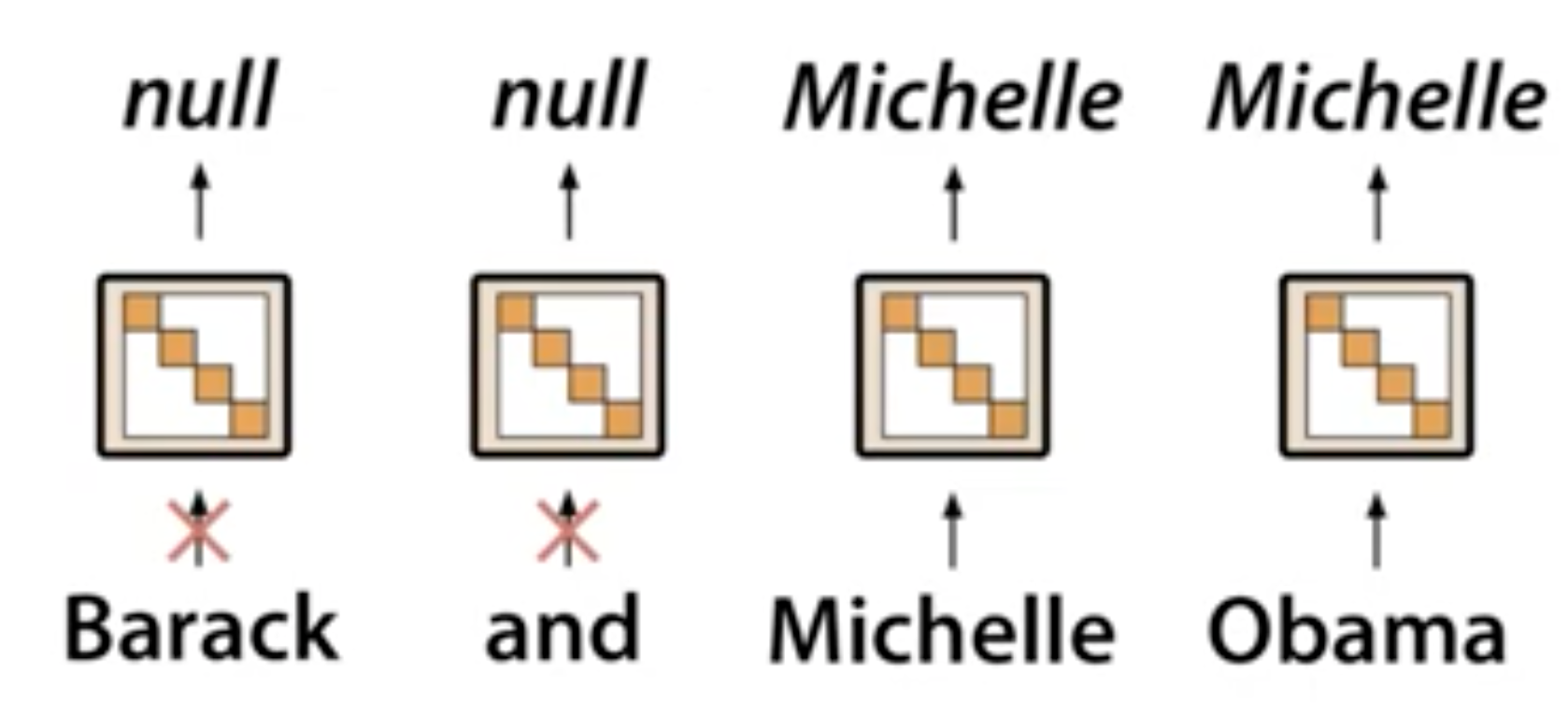
    • Multiplicative interactions between outputs

      • shift SSM output ↔ V
        • s local multiplicative interactions in linear attention
        • depending on the size of the hidden state
      • Q ↔ diagonal SSM output
        • comparisons between tokens over the entire sequence

• H3가 어떻게 associative recall문제를 해결하는가

  • 예시

    $a:4 \ \ c:2 \ \ b:3\ \ c:\ \ \rightarrow \ ??$

    

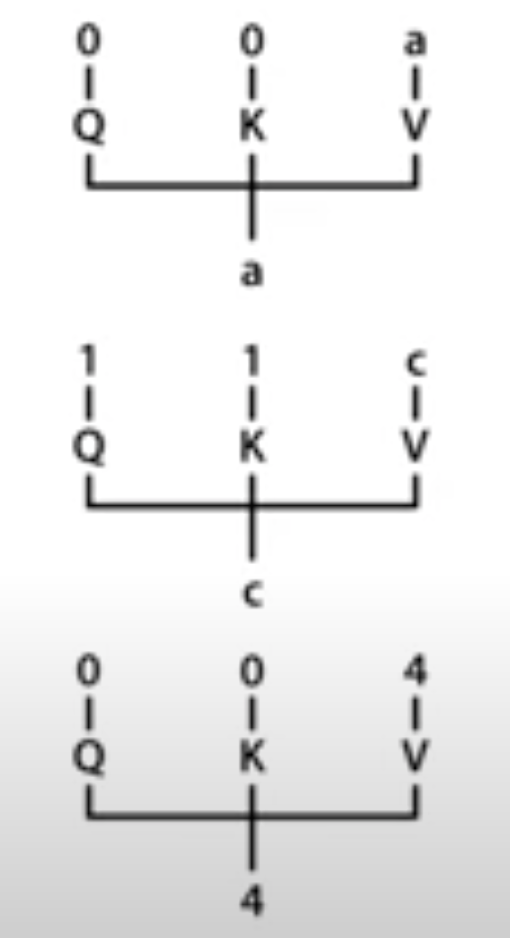
    • c를 맞추기 위해 Q, K 는 c가 value에 들어올때 만 1, 1로 활성화 됨

      

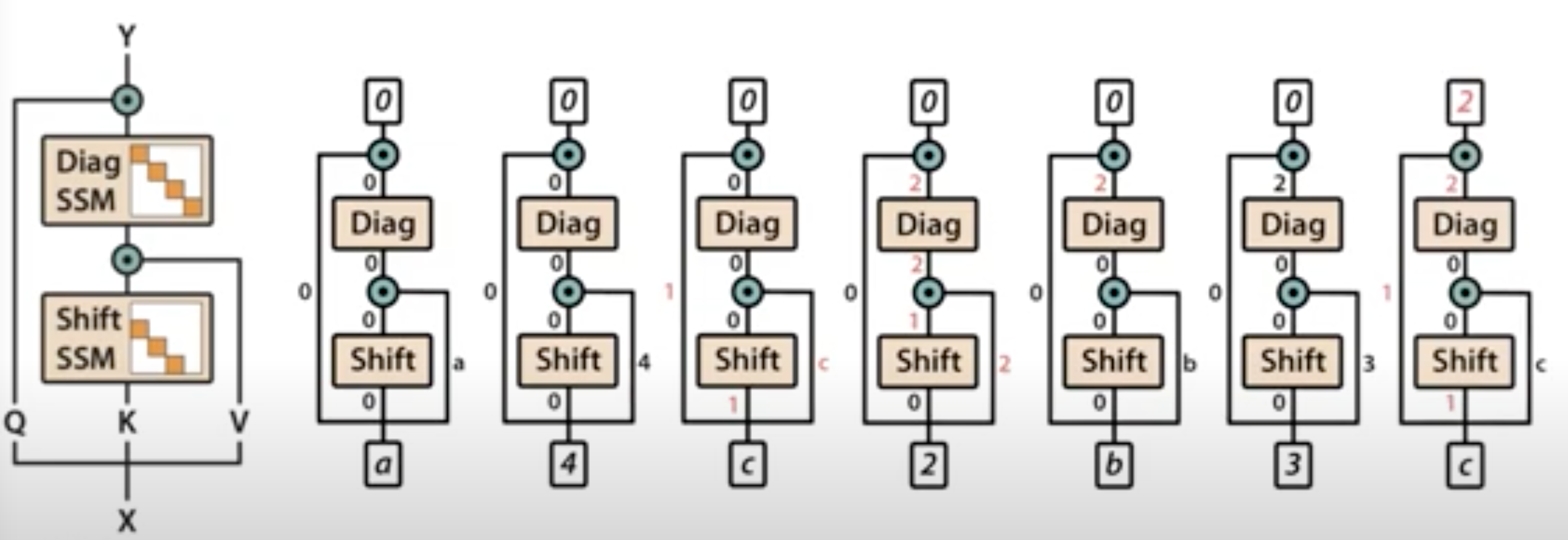
    • 3번째 블록에서 c가 value에 입력

      • Q, K 가 1, 1로 활성화 되었지만 shift SSM은 이전 단계인 4의 정보를 담고 있어 0 반환

    • 4번째 블록에서 2가 value에 입력

      • Q, K는 0, 0으로 비활성화
      • shift SSM이 c의 K 정보를 담고 있어 1을 반환
      • multiplicative interaction을 통해 diag SSM에 2입력
      • diag SSM은 global정보 기억하므로 2 반환
      • 마지막에 만난 Q가 0값으로 가지고 있어 output은 0

    • 5번째 블록에서 b가 value로 입력

      • diag SSM이 2값을 기억하고 있더라도 Q값이 0이어서 output은 0
      • 이런 방식으로 b에 대한 잘못된 값을 예측하는 것을 방지

    • 7번째 블록에서 c가 value로 입력

      • Q, K 가 1, 1로 활성화
      • shift block은 local정보를 전달하므로 이전 토큰 3입력 시 담아둔 0값 출력
      • diag block에서 global 정보였던 2를 출력
      • Q값인 1과 multiplicative interaction을 통해 최종적으로 output 2

  • 각각의 H3 레이어가 single key값에 대한 정보를 저장하게 됨

    • H3 레이어 개수 : model width

• Quality Gap 줄이기

  • acc

    Model	ACC
    Transformer	100.0
    S4D	38.8
    GSS	19.8
    H3	98.4

  • perplexity

    Model	PPL(OWT)
    Transformer	20.6
    S4D	24.9
    GSS	24.0
    H3	21.0
    H3 + 2attn (hybrid)	19.6

FlashConv

• efficiency gap을 줄이기 위함

• long convolution (long SSMs) with FFT convolution

  • FFT convolution (Fast Fourier Transform conv)
    
    # y = u * k
u_f = torch.fft.fft(u) # input signal
k_f = torch.fft.fft(k) # convolution kernel
y_f = u_f * k_f. # pointwise multiply
y = torch.fft.ifft(y_f)# inverse FFT

    -  O(NlogN)의 시간복잡도
    -  naive attention보다 느린 속도

• 속도를 높이기 위해서
  1) kernel fusion
  y = fused_fft_conv(u,k)
  - 위의 모든 연산 한번에
  - SRAM 환경에 적합
  - 적은 memory I/O

  2) Block FFT

  $F_N = P(I_{N_2}\otimes F_{N_1})P^{\top}D(I_{N_1}\otimes F_{N_2})P$

  • tensor decomposition of FFT operation

  • $F_N$ : FFT of length N
    $F_{N_1},F_{N_2}$ : shorter FFT
    $D$ : diagonal matrix
    $P$ : permutation

    → FFT 연산을 행렬 연산으로 변형
    

  3) State Passing : long sequence로 scaling

  • 4K, 8K보다 긴 입력을 받아서 연산하는 과정

  • 긴 입력을 4K, 8K 길이로 잘라 chunk를 순서대로 입력하기 (recurrent view)
    

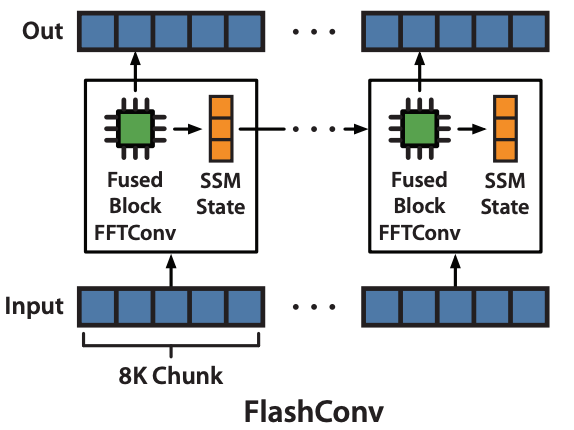
    → 첫번째 chunk에 대해 output 계산하는 과정에서 SSM state 또한 update됨
    → update된 SSM state를 다음 단계에 넘겨 다음 chunk의 output을 계산하는 과정에서 활용

• 3가지 방식 활용한 결과

  

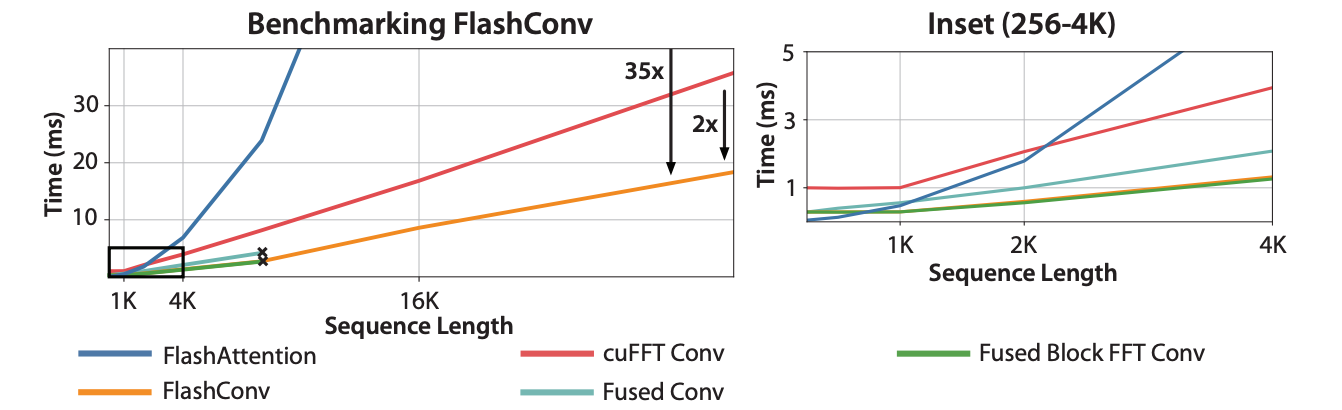
  • 짧은 input sequence에서도 (~2K) transformer에 비해 빠른 속도 확인
  • 긴 Input sequence에서 transformer에 비해 약 35배 빠른 속도
  • 긴 input sequence에서 naive SSM에 비해 약 2배 빠른 속도

요약

• 기존 Transformer의 경우 Quadratic 연산이 필요한 Attention을 활용하여 input token의 길이, 연산량에 있어 한계 존재
• Quadratic연산을 Sub-Quadratic 연산으로 대체하는 알고리즘의 필요성 대두
• 이를 위해 State Space Model (SSM) 활용 결정
• 그러나 SSM은 quality, efficiency 모두 transformer에 비해 뒤처짐
• SSM block를 활용한 H3 레이어와 FFT conv기반의 FlashConv를 활용하여 quality, efficiency 문제 모두 해결

궁금했던 점들

• 왜 이름이 hungry hungry hippo일까?
  - High-order Polynomial Projection Operators 논문의 HiPPO 알고리즘을 기반으로 연구했기 때문인 것 같다.

  • 논문 중간에 이러한 내용이 있다.

    To preserve the sequence history, HiPPO [24] projects the history on a basis of orthogonal polynomials, which translates to having SSMs whose A, B matrices are initialized to some special matrices.

    - 여기서 말하는 A, B는 SSM 연산 중 hidden state와 input sentence에 곱해지는 A, B 파라미터를 의미

  • 직교 다항식(orthogonal polynomials)을 기반으로 시퀀스의 history를 투영하는 과정에서 SSM을 특정 행렬로 초기화하는 방식을 본따온 듯..!

• 푸리에 변환과 합성곱의 관계
  • 합성곱 계산 : 매우 복잡함
  • 두 함수의 푸리에 변환 뒤 곱셈으로 합성곱을 보다 쉽게 구현할 수 있음
  • 공간 영역의 합성곱 = 주파수 영역의 곱셈
  • 공간 영역에 있는 두 함수를 모두 푸리에 변환하여 주파수 영역으로 변환한 뒤 곱셈 계산으로 간편하게 합성곱 구현 가능