[백준]11726 2xn 타일링

나는 접근법부터 틀렸지만.. 실패를 해야 발전도 하고 성장도 하는거니까 일단 기록 ㅠ
1) 일단 무조건 2x1로 다 채울 수 있고, 1x2로 가로변-1 개만큼 채울 수 있으므로 +n이 된다.
2) 1x2로 여러개를 채울 때는 가로변의 -2한 길이에서 -1을 한번 더해주면 갯수가 나온다. (고정해놓을 1x2를 제외하면 -2고 1x2가 남은 가로변에서 움직일 수 있는 길이는 n-2-1이기 때문!) 요걸 1x2, 1x4, 1x6 ... 채울 수 있을만큼 반복해줘야 한다.
3) 짝수면 1x2로 전부 꽉 채울 수 있기 때문에 +1을 더해줘야한다.

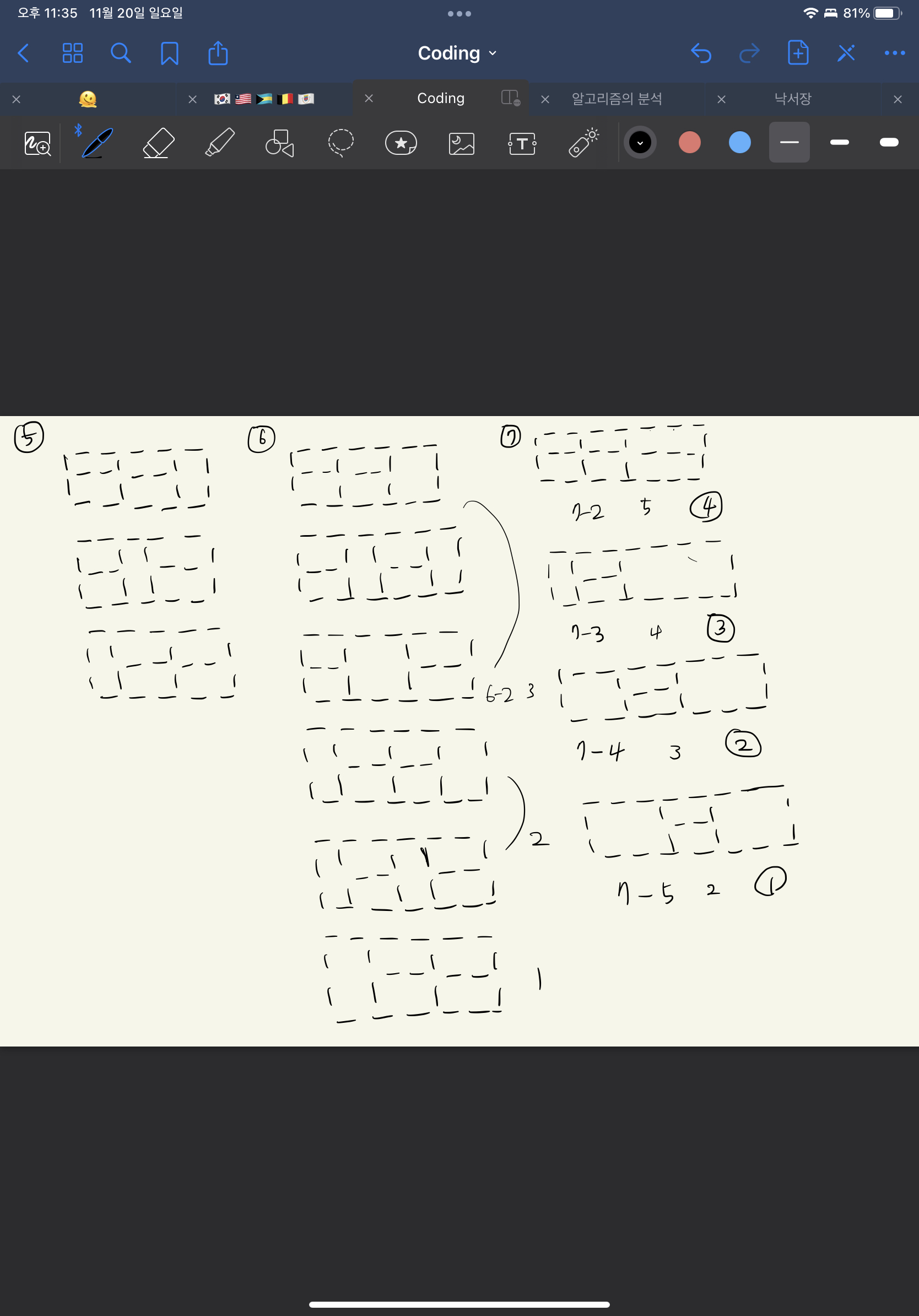
그리고 실패코드..

package baekjoon;

import java.util.Scanner;

public class Main_11726 {
    static int[] dp = new int[500];
    static int n;
    public static void main(String[] args) {

        Scanner sc = new Scanner(System.in);
        n = sc.nextInt();

        for (int i = 2; i < n; i += 2) {
            dp[n] += dp(i);
        }
        System.out.println(n+dp[n]);


    }
    public static int dp(int i) {
        int count=0;
        for (int j = i; j <= (n - 2); j++) {
            count += (n-j-1);
            System.out.println(n + "-" + j + "-1 = "+(n-j-1));
        }
        System.out.println(count);
        return count;
    }
}

그래서 결국 풀이의 도움을 받았다..

package baekjoon;

import java.util.Scanner;

public class Main_11726 {
    public static void main(String[] args) {

        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();

        int[] dp = new int[1001];
        dp[1] = 1;
        dp[2] = 2;
        for (int i = 3; i <= n; i++) {
            dp[i] = (dp[i - 1] + dp[i - 2]) % 10007;
        }
        System.out.println(dp[n]);
    }
}

규칙을 찾으면 아주 쉽게 풀 수 있는 문제였다. 나는 오만 잡다한 방법으로 끙끙댔는데 풀이보고 좀 현타왔다.
1 > 2 > 3 > 5 > 8 > 13 ..
1+2 = 3
2+3 = 5
3+5 = 8
5+8 = 13
규칙을 찾으면 금!!!방 풀 수 있다.

마지막으로 이건 고뇌의 흔적.. 코테 잘 못 푼다고 기죽지 말자!!! 이렇게 공부하는거지 모 🤤