[백준]9095 1, 2, 3 더하기

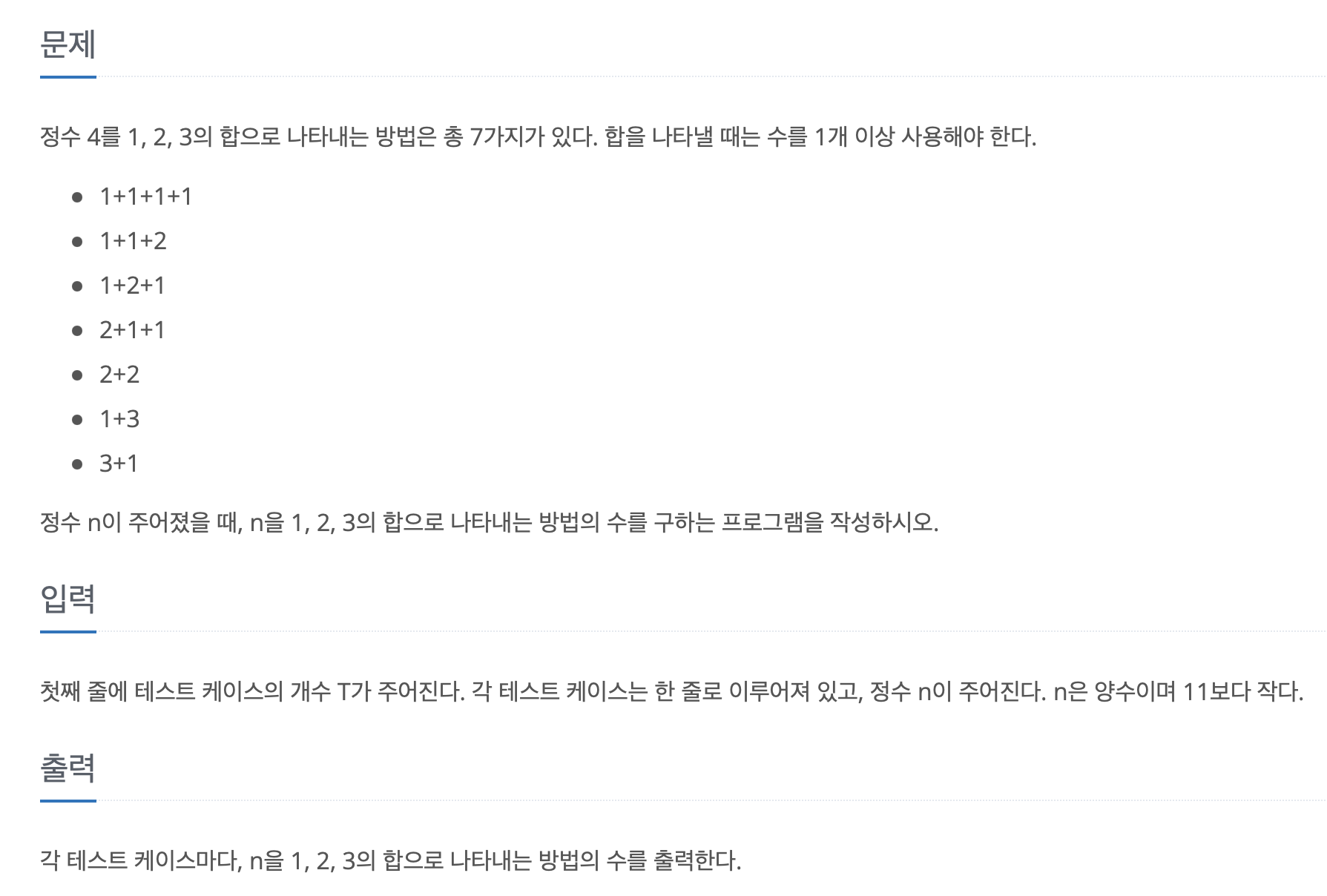
나는 dp에 능숙하지 못해서 일단 쓰고보는 타입.. 나름의 규칙을 찾아보니 직전 배열들에 저장된 조합들에 1씩만 더하면 원하는 조합이 된다는 걸 알았다.

예를 들면 (1은 조합이랄게 없으니 패스하고)
dp[2] = dp[1]에 1씯 더하고 (1 1) 조합의 일부분인 2
dp[3] = dp[2]에 1씩 더하고 (1 1 1, 2 1) dp[1]에 2씩 더하고 (1 2) 조합의 일부분인 3
dp[4] = dp[3]에 1씩 더하고 (1 1 1 1, 1 2 1, 2 1 1, 3 1) dp[2]에 2씩 더하고 (1 1 2, 2 2) dp[1]에 3씩 더하고 (1 3)
dp[5] = dp[4]에 1씩 더하고 (1 1 1 1 1, 1 2 1 1, 2 1 1 1, 3 1 1) dp[3]에 2씩 더하고 (1 1 1 2, 1 2 2, 2 1 2, 3 2) dp[2]에 3씩 더하고 (1 1 3, 2 3) dp[1]에 4를 더해야 하는데 4는 조합의 일부가 아니고 이미 dp[2]에서 충족이 됐을 것이므로 넘어간다.

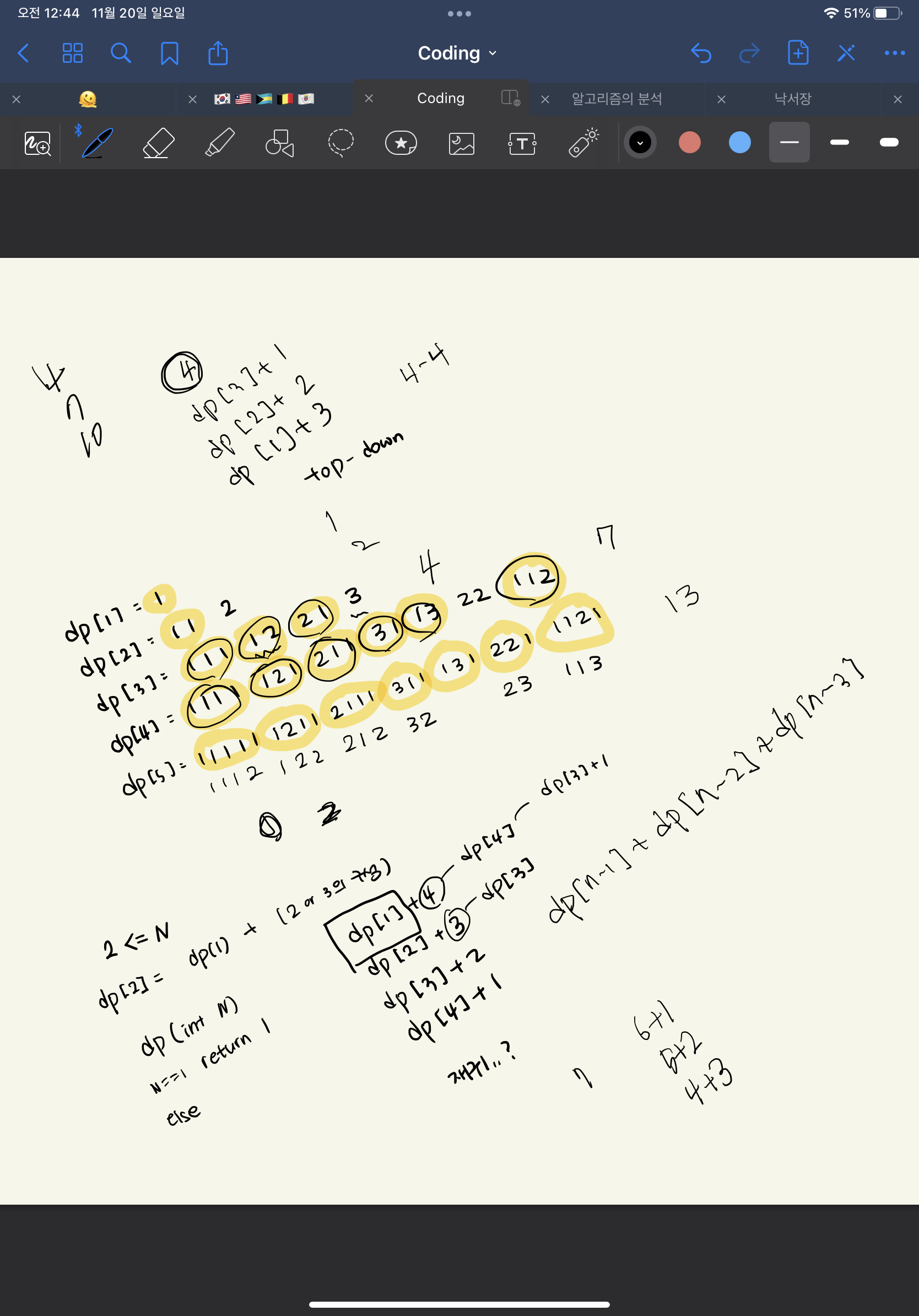
점화식이 dp[n] = dp[n-1]+dp[n-2]+dp[n-3] 일 것 같은..
요런 규칙을 찾았다 이걸 뭔가 dp스럽게 코드를 짜면 될 것 같았는데
실 ! ! !! 패! ! ! !! 🤤 너무 어려워

방법1

package baekjoon;

import java.util.Scanner;

public class Main_9095 {
    static int[] dp = new int[11];
    public static void main(String[] args) {

        Scanner sc = new Scanner(System.in);
        int N = sc.nextInt();

        int[] array = new int[N];

        dp[1] = 1; // (1) - 1가지
        dp[2] = 2; // (1+1, 2) - 2가지
        dp[3] = 4; // (1+1+1, 1+2, 3) - 4가지
        for (int i = 0; i < N; i++) {
            int start = sc.nextInt();
            array[i] = start;
            for (int j = 4; j <= start; j++) {
                dp[j] = dp[j-1]+dp[j-2]+dp[j-3];
            }
        }
        for (int n : array) {
            System.out.println(dp[n]);
        }
    }
}

방법2

import java.util.Scanner;

public class Main {
	public static int[] dp;
	public static int[] tmp;

	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);

		dp= new int[11];
		
		dp[1] = 1;
		dp[2] = 2;
		dp[3] = 4;
		
		int tcase = sc.nextInt();
		tmp= new int[tcase];
		for(int i=0; i<tcase; i++) {
			int a = sc.nextInt();
			tmp[i]=a;
			dp(a);
		}
		for(int j=0; j<tmp.length; j++) {
			System.out.println(dp[tmp[j]]);
		}
		
	}


	public static int dp(int num) {
		if(dp[num]!=0)	return dp[num];
		return dp[num] = dp(num-3) + dp(num-2) + dp(num-1) ;
	}
}

풀이와 점화식은 위에 내용이 맞았다! 이걸 코드로 풀어내는 데 아직 미숙했던 것 같다 너무 헷갈려잉 ... 암튼 그래도 큰 발전 !!!