
함수안의 함수?
처음 자바스크립트를 접했을 때를 생각해보면 정말 생소한 단어들을 많이 접했던 것 같다. 그중 특히 생소하고 이해되지 않았던 그 단어 Closure 😑. 자바스크립트 개발자로 면접을 다닐때에도 클로저라는 개념을 물어보는 경우가 많았던것 같다. 그때마다 기계적으로 함수안의 함수라고 답하기만 했다. 사실 틀린말은 아니다. 하지만 개념을 안다고 클로저를 잘 활용하는건 아니지 않는가? 그렇게 클로저라는 개념을 배우고도 실제로 활용하는 방법을 익힐때까진 꽤 시간이 필요했던것 같다. 그럼 실제로 Closure를 활용해 소수 생성기를 직접 만들어보자. 그것도 Memoization기법을 적용해서 😉
그래 도대체 Closure 가 뭐야?
MDN 를 참조해보자.
A closure is the combination of a function bundled together with references to its surrounding state (the lexical environment).
클로저는 주변 상태(렉시컬 환경)에 대한 참조와 함께 감싸여진 함수의 결합이다.
큰일났다. 무슨말인지 너무나 어렵다 😯. 사실 클로저의 개념은 실행 컨텍스트(poiemaweb님 블로그) 개념을 익히면 자연스럽게 이해할 수 있는 기법이다. 하지만, 자바스크립트를 많이 다뤄보지 않은 사람은 둘 다 쉽게 이해하기 힘든 개념이다. 그러니까 우선 간단한 소스코드로 클로저와 친해져보자.
function addClosure (_a) { // Outer function
let a = _a;
return function (b) { // Inner function
return a + b;
}
}
const add = addClosure(10);
add(5); // 15
add(10); // 20자 여기 Closure 를 활용한 간단한 add 함수를 구현해봤다. addClosure() 를 호출해 함수 내부변수 a를 초기화 시켜준다. 그후, b 를 입력받아 a와 덧샘을 하는 함수를 반환해주자. 우리의 상식으로는 addClosure() 함수가 끝나면 내부의 변수와 상태는 반환되는것이 당연하다. 그런데 생성된 클로저를 실행해보면 거짓말처럼 a의 상태를 기억하고 새로 입력받은 b와 덧샘을 수행하는걸 볼 수 있다. 간단하게 설명하면 이렇듯 클로저는 자신이 생성될 때의 환경 (Lexical Environment)를 기억하는 함수인 것이다. 더 자세한 설명은 다음에 실행 컨택스트를 다루면서 하겠다. 😣
N번째 소수 구하기
우선 소수의 정의를 위키백과 에서 찾아보자.
소수(Prime Number)는 1과 그수 자신 이외의 자연수로는 나눌 수 없는, 1보다 큰 자연수이다.
N번째 소수를 구하는 알고리즘은 여러가지가 있는데 그중 우리는 간단하게 초등학교때 배웠던 에라토스테네스의 체 를 이용해 구현해보자.
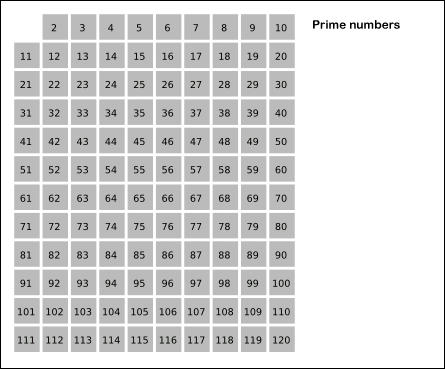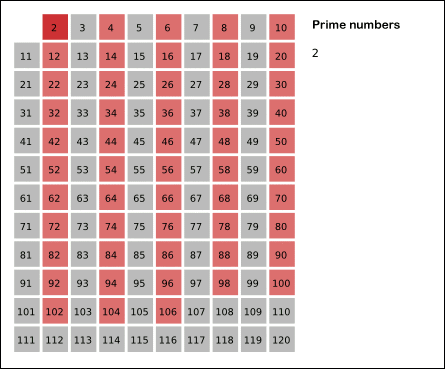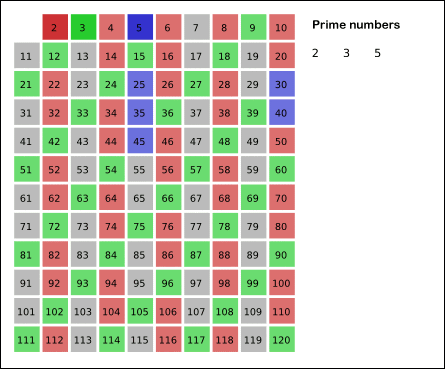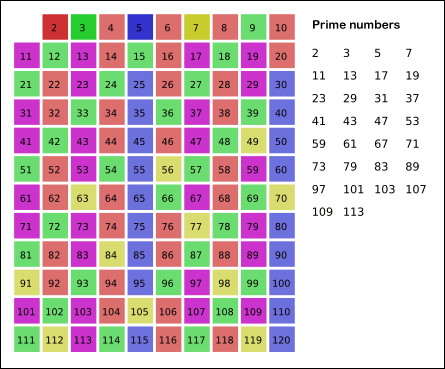
에라토스테네스의 체는 위의 그림과 같이 2, 3, 5, 7 ... 같이 소수를 순서대로 나눠보면서 나누어 떨어지는수가 없다면 소수로 판별하는 알고리즘이다. 이때 입력되는 수 n의 제곱근까지만 연산하도록 만들면 더욱 효율적인 연산을 할 수 있다.
// 소수 판별 함수
function isPrimeNumber (n, primeNumbers) {
for (const v of primeNumbers) {
if (n % v === 0) {
return false;
}
// 효율적인 연산을 위해 제곱근까지만 연산
if (Math.sqrt(n) < c) {
return true;
}
}
return true;
}위 함수는 소수인지 판별이 될 수 n과 지금까지 연산된 소수를 받아 소수를 판별하는 함수다.
function closurePrimeNumber () {
// 소수를 저장할 저장소
const primeNumbers = [2]
return function (n) {
// 이미 n번째 소수를 찾았다면
if (primeNumbers.length >= n) {
// n번째 소수를 전달해준다.
return primeNumbers[n - 1]
}
// 아직 찾지 못했다면
// 가장 마지막수를 선택해서 1씩 더하면서 해당수가 소수인지 판별한다.
let targetNumber = primeNumbers[primeNumbers.length - 1]
while (primeNumbers.length < n) {
targetNumber += 1
// 해당수가 소수인지 판별하고
if (isPrimeNumber(targetNumber, primeNumbers)) {
// 소수일경우 소수 저장소에 저장한다.
primeNumbers.push(targetNumber)
}
// n번째 소수를 찾았다면
if (primeNumbers.length >= n) {
// 해당 수를 사용자에게 전달한다.
return targetNumber
}
}
}
}그리고 여태까지 계산된 소수를 저장할 primeNumbers 를 담은 Outer Function 인 closurePrimeNumber를 만들어주자. 해당 함수의 반환값은 숫자 n이고 해당 함수의 역할은 n번째 소수를 판별해서 전달해주는 역할을 한다.
const genPrimeNumber = closurePrimeNumber()
genPrimeNumber(10000) // 1
genPrimeNumber(10001) // 2
/*
* 10000번째 소수: 104729
* 1 function: 12.047ms
*
* 100001번째 소수: 104743
* 2 function: 0.536ms
*/closurePrimeNumber()를 실행하게되면 primeNumbers를 클로저로 감싼 함수를 반환하게 되고, 반환된 함수를 실행하면 n번째 소수를 찾을 수 있다. 이때 primeNumbers는 클로저 내부에서 캐싱되어 있기 때문에 이미 찾은값은 생략하고 빠르게 다음 소수를 찾을 수 있다.
결론
이렇게 클로저를 활용해서 N번째 소수를 찾는 코드를 만들어봤다. 사실 우리가 알게 모르게 클로저의 특성을 이용해서 개발을 할때가 많을것이다. 예를들어 비동기함수를 만들때라던가 위 예제처럼 연산캐싱을 하던가 외부에서 내부변수에 접근을 차단하도록 만들때 쓴 경험이 있을것이다. 여튼 이 글이 조금이라도 도움이 될 수 있길 바라며 위에서 만든 함수를 실제 채험해볼 수 있는 간단한 웹 어플리케이션을 만들어봤다. 한번 채험해 보면 좋을것 같다 😁.
좋아요와 댓글은 큰힘이 됩니다.
마지막으로 새로운 블로그를 만들었습니다. 한번씩 찾아와 주시면 정말 큰힘이 됩니다 🥰
