Segment Tree 개요
Segement Tree란?
- 세그먼트 트리는 구간의 정보를 저장하는 자료구조
- 세그먼트 트리를 사용하면 구간의 합, 최솟값, 최댓값을 만에 구할 수 있다
- Full Binary Tree이다
- 1차원 배열로 구현하면 효율적이다
Segment Tree를 시작하기 전에 알아야 할 것
(1) 노드 번호 부여하기
- Root : 1번
- left child : 부모 x 2
- right child : 부모 x 2 + 1
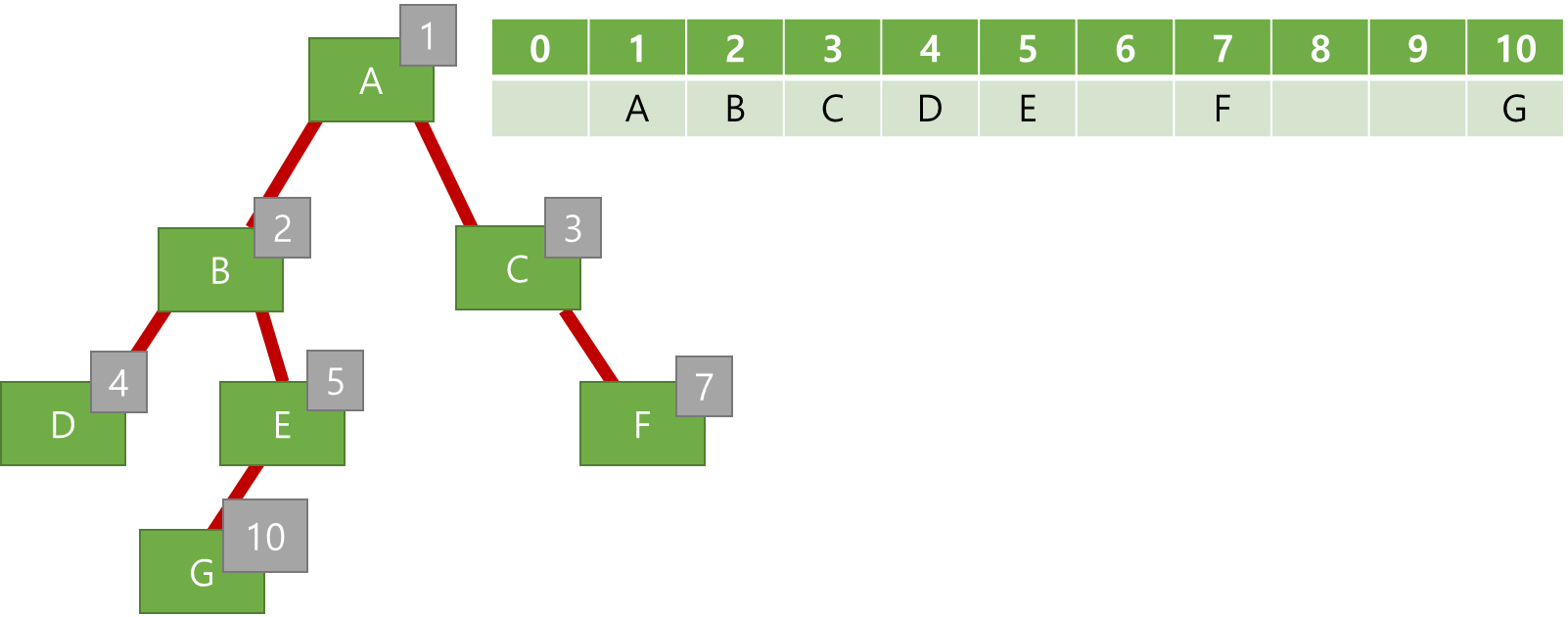
(2) Tree Traveral
1차원 배열로 구현한 트리 탐색
예) 전위 순회(preorder traversal)
#include <iostream>
using namespace std;
char tree[11];
void init();
void dfs(int index);
int main()
{
init();
dfs(1);
return 0;
}
void init()
{
tree[1] = 'A';
tree[2] = 'B';
tree[3] = 'C';
tree[4] = 'D';
tree[5] = 'E';
tree[7] = 'F';
tree[10] = 'G';
}
void dfs(int index)
{
if (index >= 11) return; // 트리의 범위를 벗어나면 return
if (tree[index] == '\0') return; // 자식이 없으면 리턴
cout << tree[index] << ' ';
dfs(index * 2); // left child
dfs(index * 2 + 1); // right child
}예) 노드 총 개수 구하기
int getCount(int index)
{
if (index >= 11) return 0; // 이게 뭘 뜻함? => 없는 자식 가리킬 때
if (tree[index] == '\0') return 0;
int lcount = getCount(index * 2); // left child
int rcount = getCount(index * 2 + 1); // right child
return lcount + rcount + 1;
}Segment tree 기본 원리 이해
1. 구간에서의 최솟값 구하기
(1) 세그먼트 트리 구축
여러 구간의 최솟값들을 미리 구해두기
(2) Query 동작
구간 A~B를 입력받으면, 미리 구해둔 최솟값들을 이용하여 구간의 최솟값을 빠르게 구함
예시) 다음과 같이 미리 구간의 최솟값을 구해놓은 상태


Q. 1~8의 최솟값은?
- 전체를 살펴볼 필요가 없음
- = 500원
Q. 4~8의 최솟값은?
- = 500원
Q. 3~6의 최솟값은?
- = 500원
2. 구축된 세그먼트 트리에서 이해하기
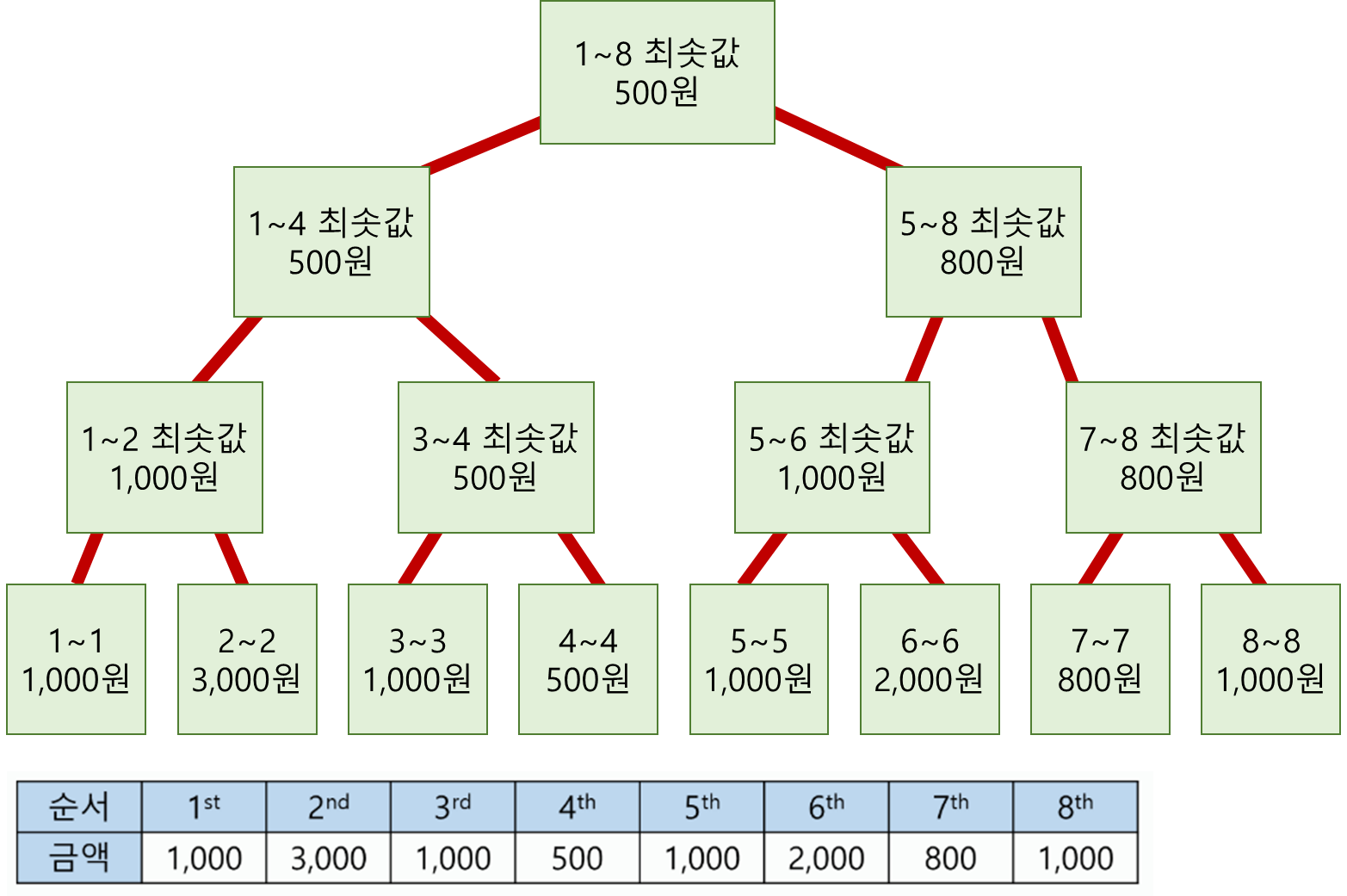
위 그림처럼 8개의 데이터에 대해, 구간을 절반씩 나누어 해당 구간에서의 최솟값을 노드에 기록하였습니다. 특정 구간에서의 최솟값 쿼리가 들어오면, 몇 개의 노드가 필요한지 개수를 구해봅시다.
> [Query] 4 ~ 8
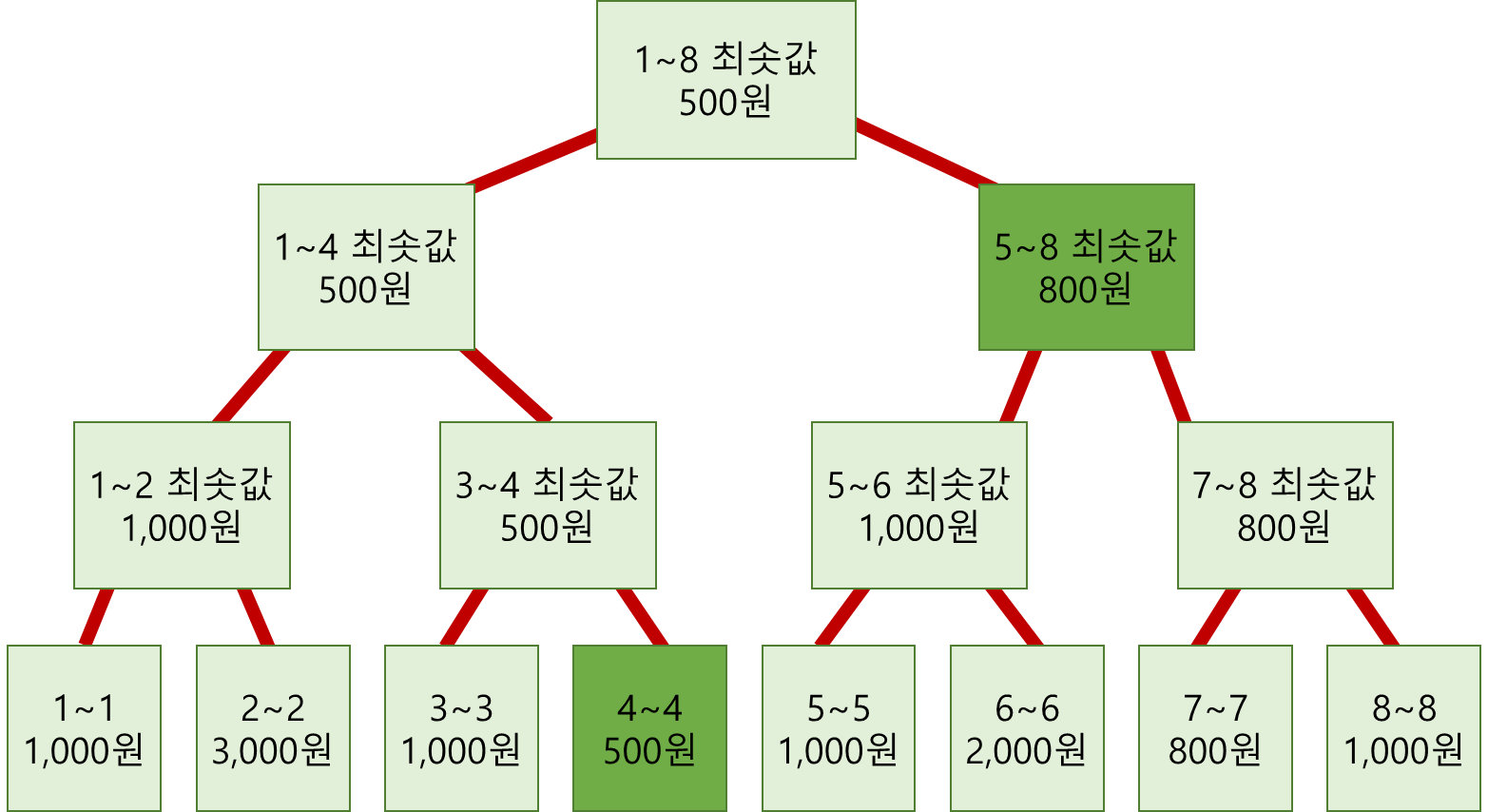
- 4 ~ 8 최솟값은 4 ~ 4 값과 5 ~ 8 최솟값 두 개의 노드가 필요합니다.
> [Query] 3 ~ 7
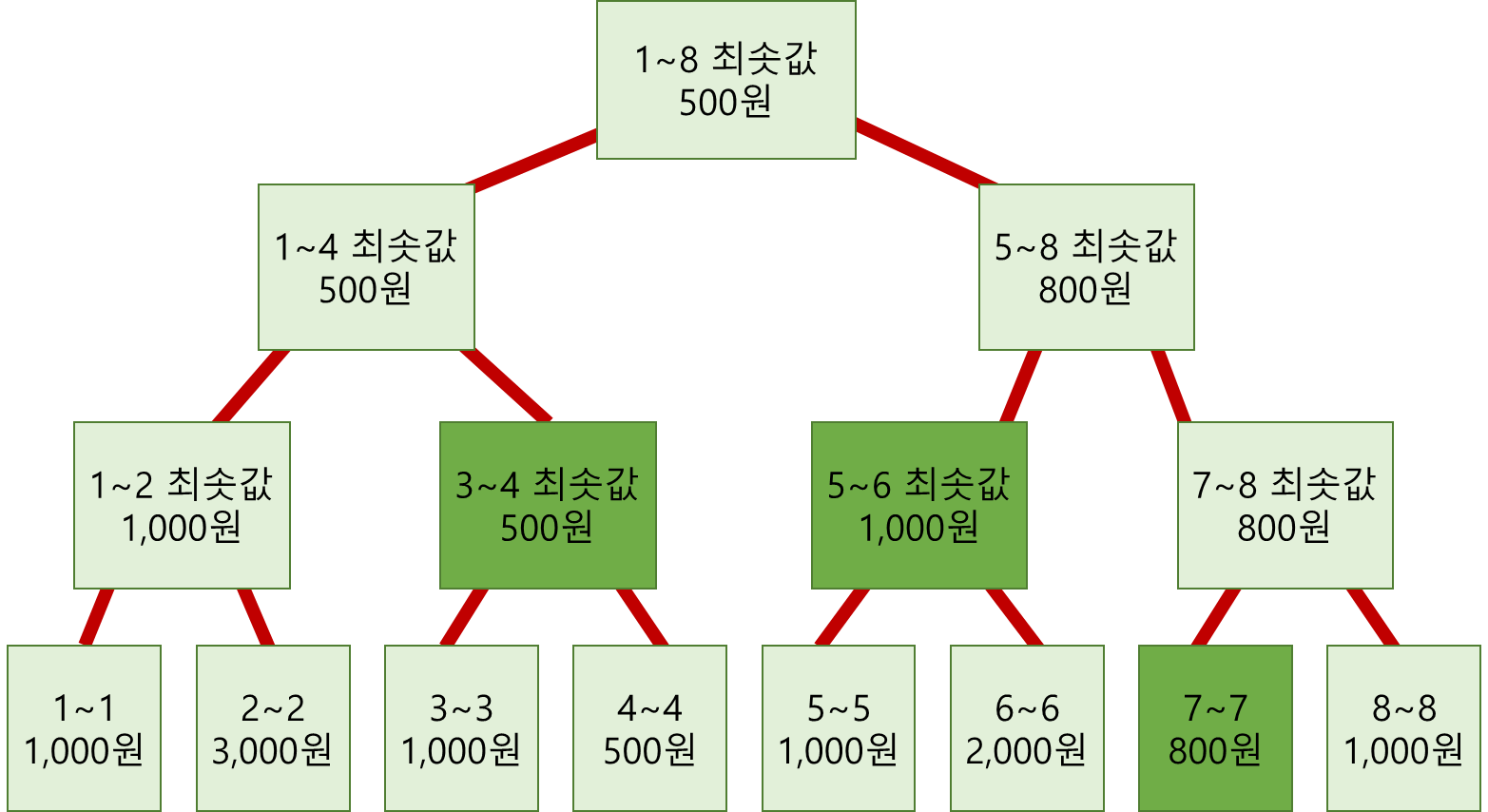
- 3~7 최솟값 = min(3~4 최솟값, 5~6 최솟값, 7~7 최솟값) 입니다.
- 세 개의 노드가 필요합니다.
> [Query] 2 ~ 7
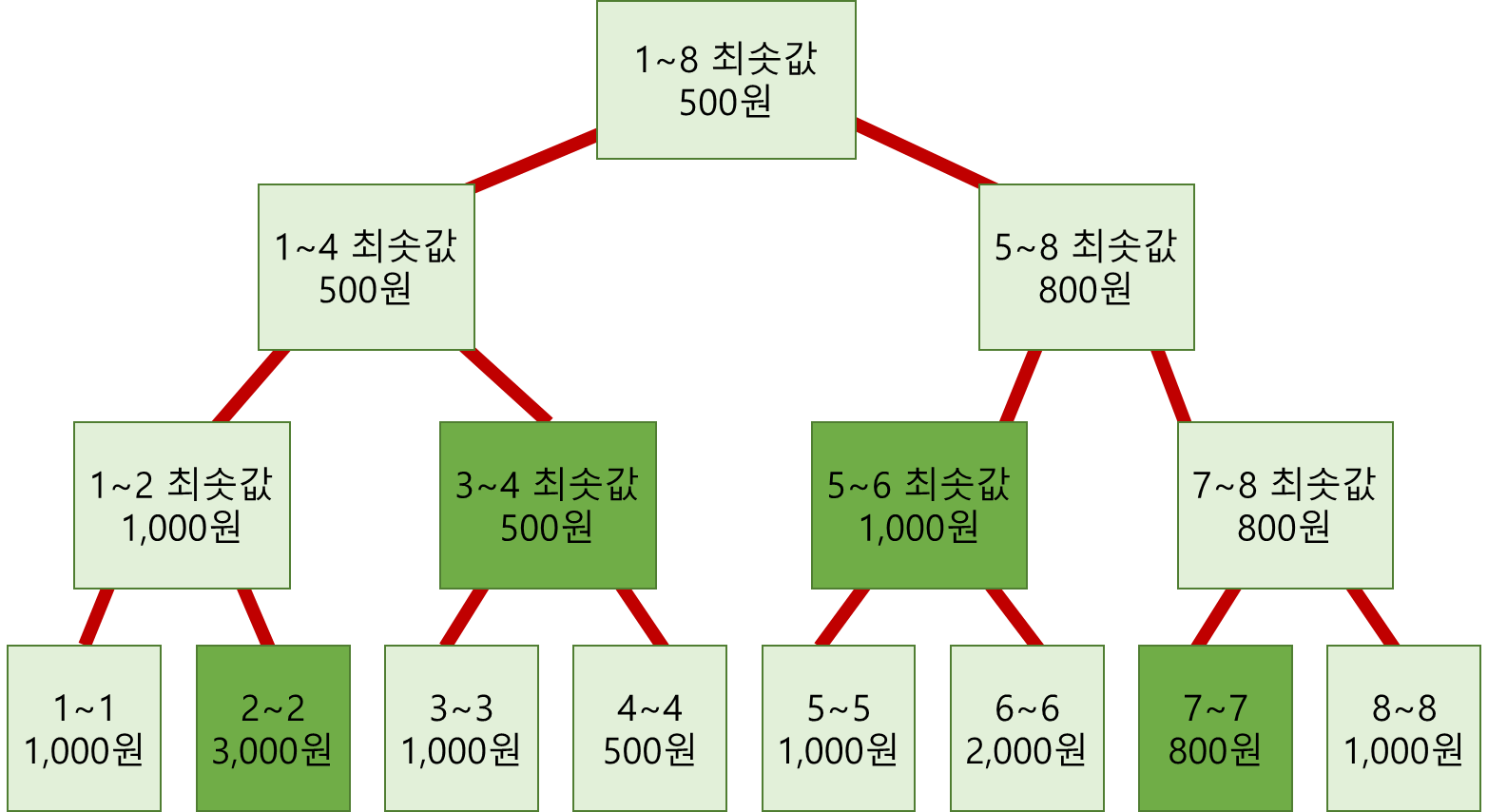
- 2~7 = min(2~2, 3~4최솟값, 5~6최솟값, 7~7)
- 4개의 노드
> [Query] 1 ~ 6
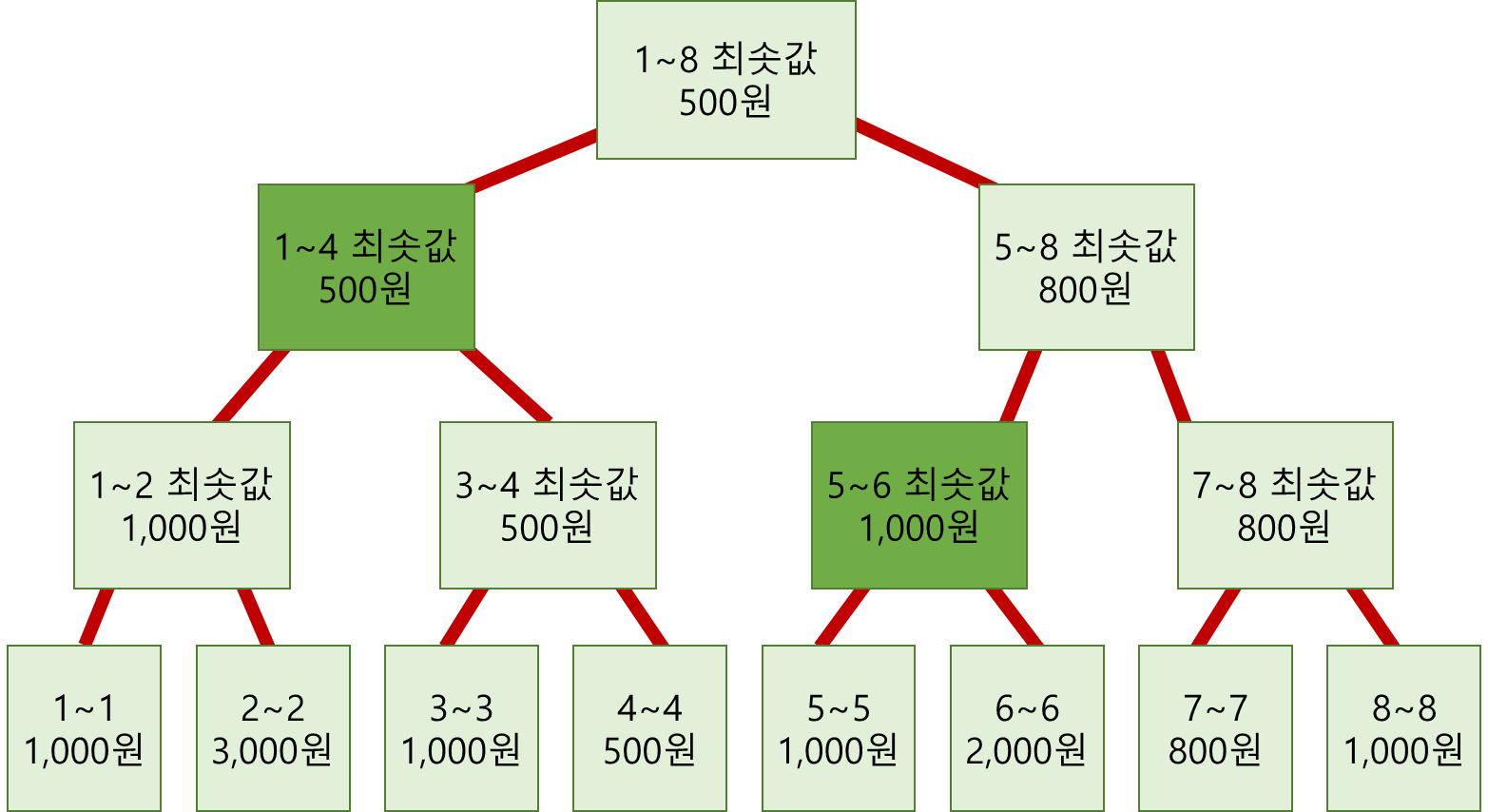
- 1~6 = min(1~4 최솟값, 5~6 최솟값)
- 두 개의 노드
Segment Tree 구현 : 최솟값
세그먼트 트리의 구현은 Construction, Query, Update로 나뉩니다.
1) Construction : 세그먼트 트리 구축하기
2) Query : 범위로 구간 정보 알아내기
3) Update : 원소 값 변경 처리하기
(1) Construction
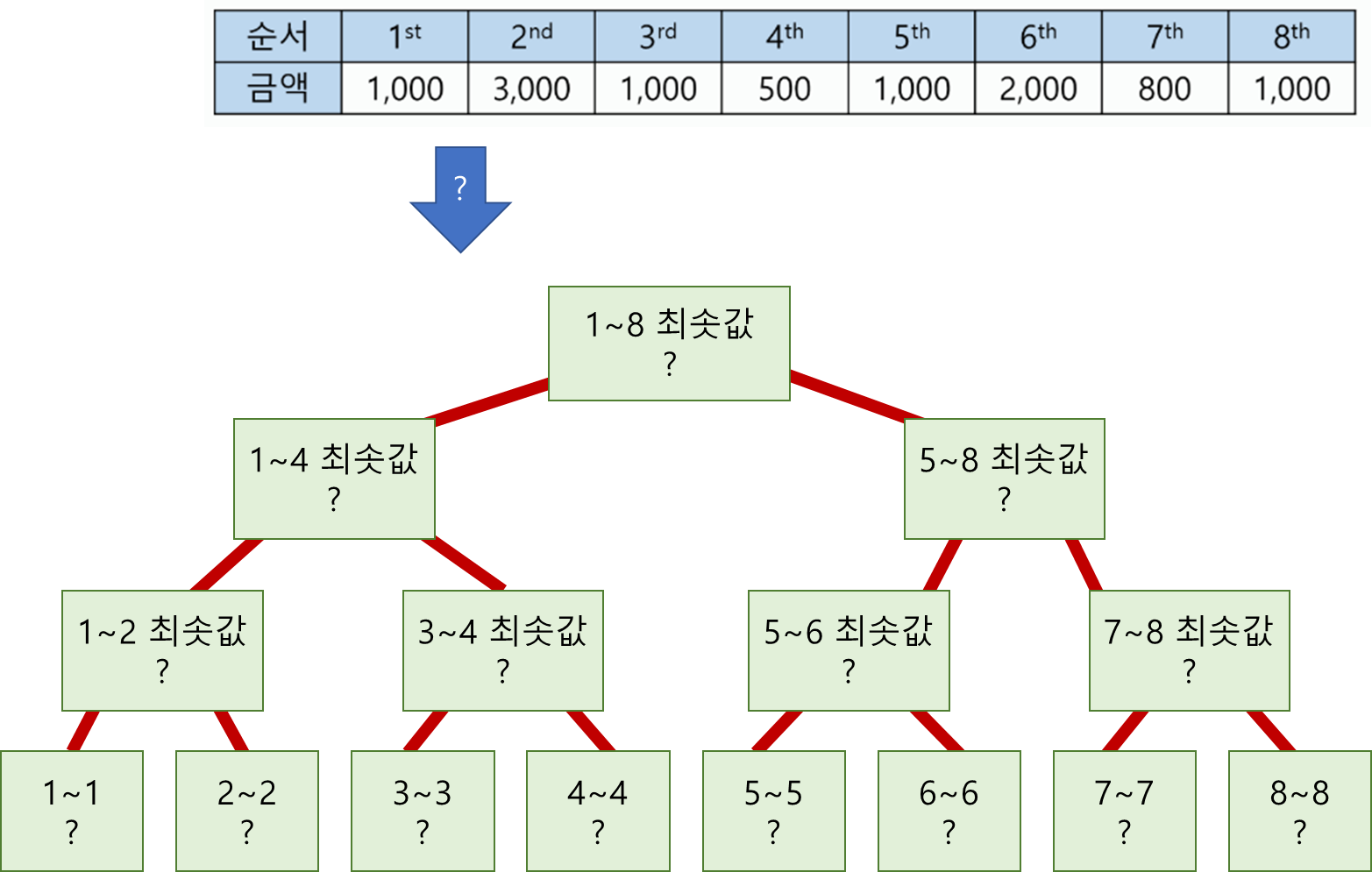
1) Leaf Node(왼쪽 범위 == 오른쪽 범위)를 만나면, 해당 인덱스의 값을 그대로 세그먼트 트리에 기록
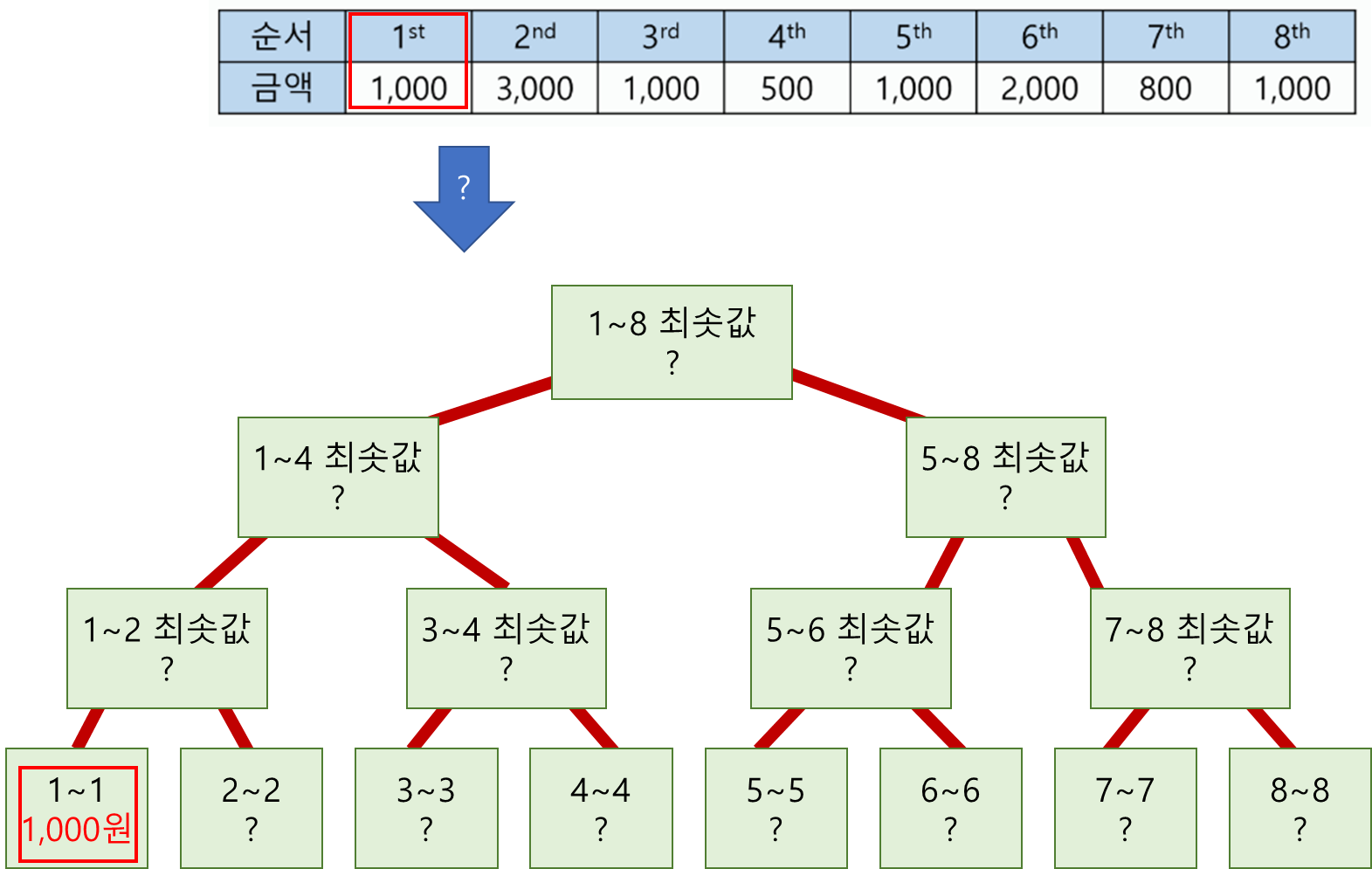
2) 왼쪽과 오른쪽 자식노드 탐색이 끝나고 부모 노드로 돌아와서 둘중 더 작은 값을 현재 노드값으로 결정
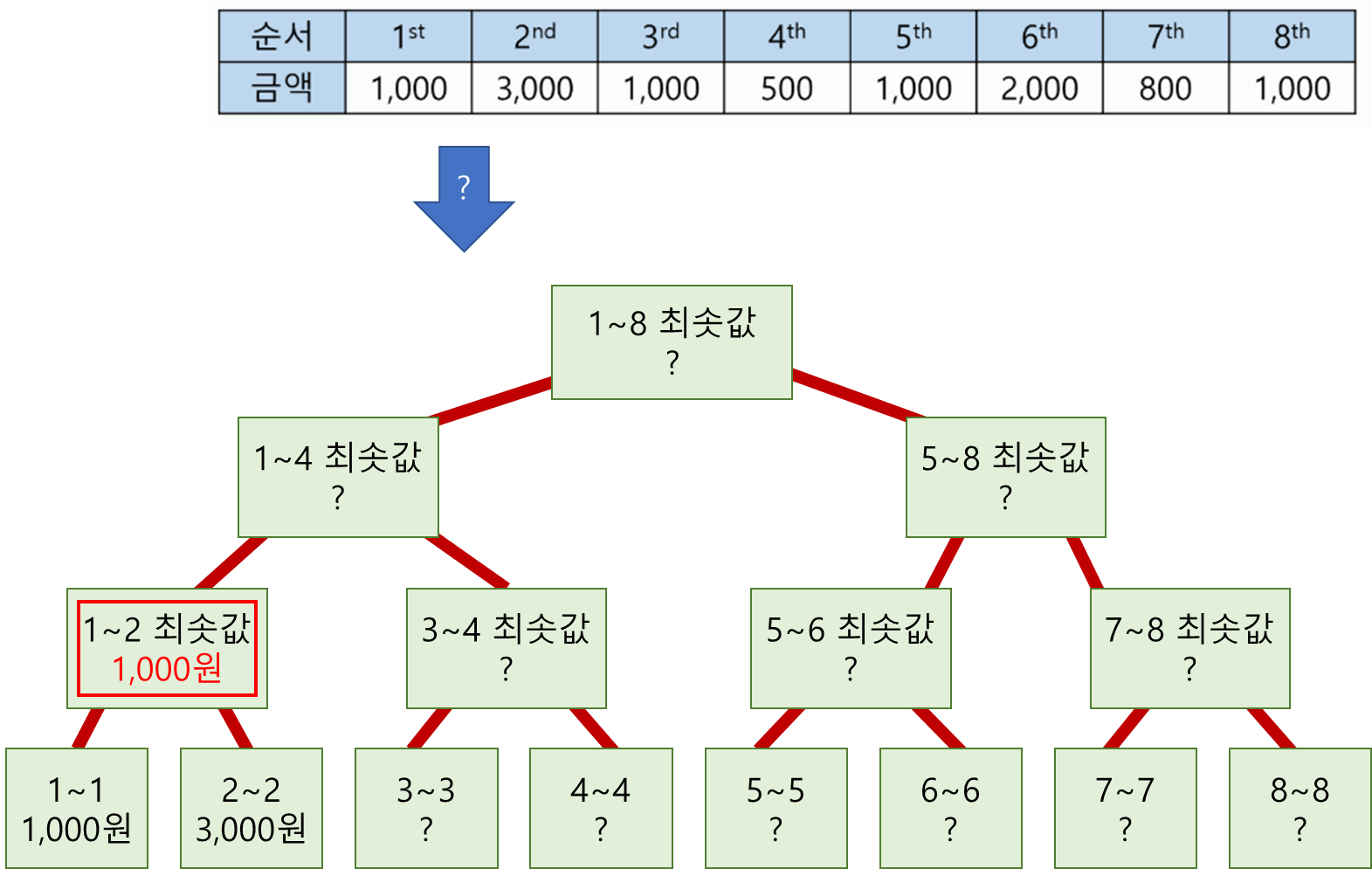
3) 재귀적으로 호출하면 결과는 다음과 같다
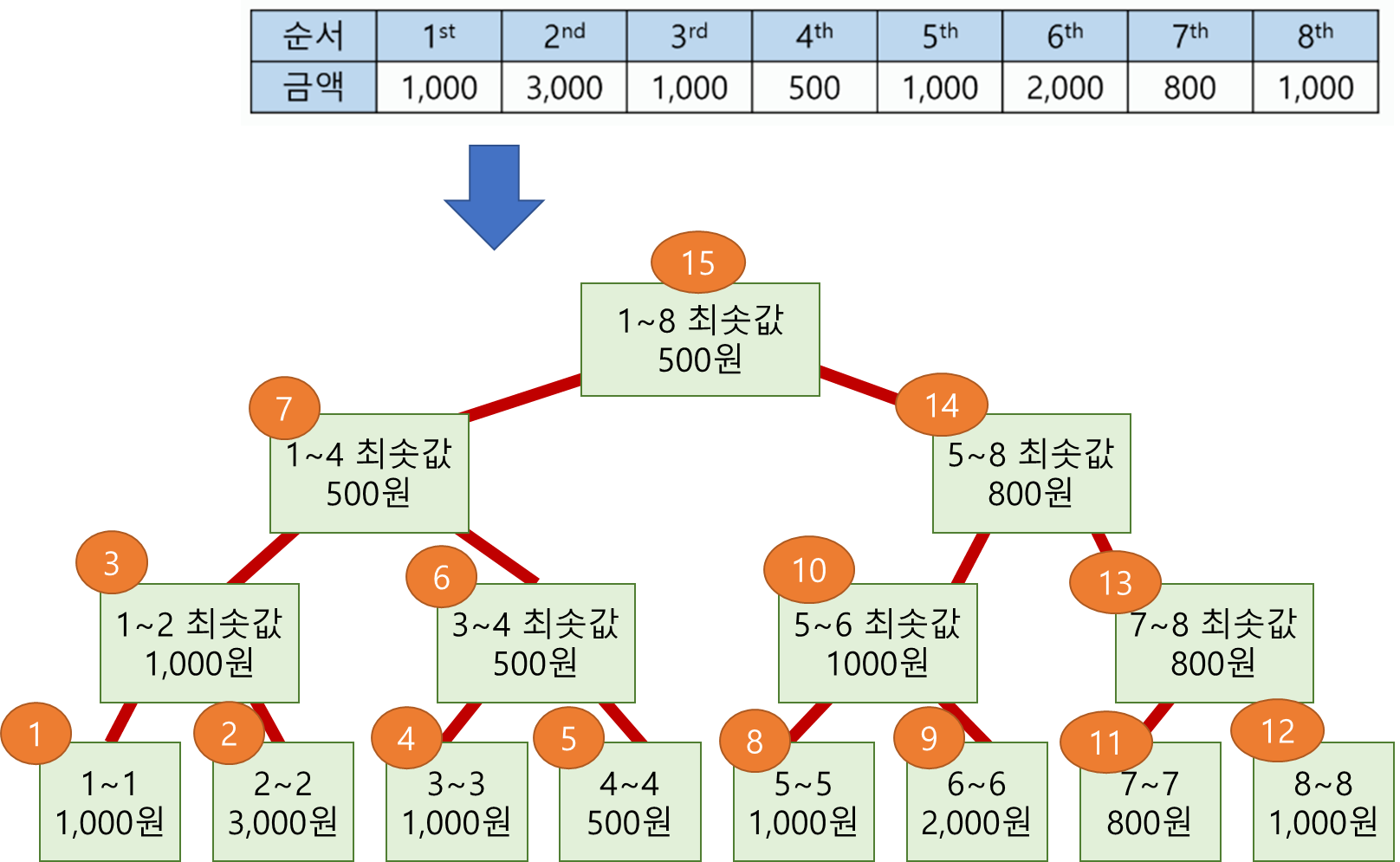
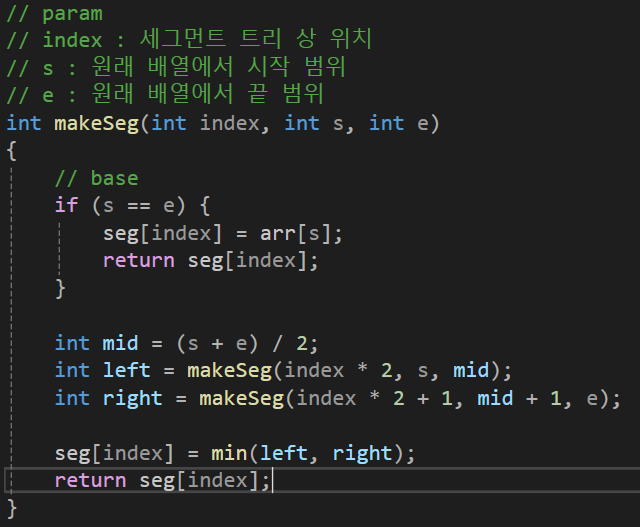
구현 코드:
- seg는 1차원 배열로, 그 크기는 N보다 커야함은 당연합니다.
- N = 8인 경우, 8 + 4 + 2 + 1 = 15입니다.
- 입니다.
- 따라서 세그먼트 트리 사이즈는 4N만 잡아도, 안전하게 사용 가능합니다.
2. Query
현재 범위가 쿼리 범위 안에 완벽히 들어오는지 확인
-> 완벽히 들어오면 리턴
-> 들어오지 않으면 범위 절반으로 쪼개서 다시 확인
이런식으로 검사하기 때문에, 시간복잡도
구현 코드:
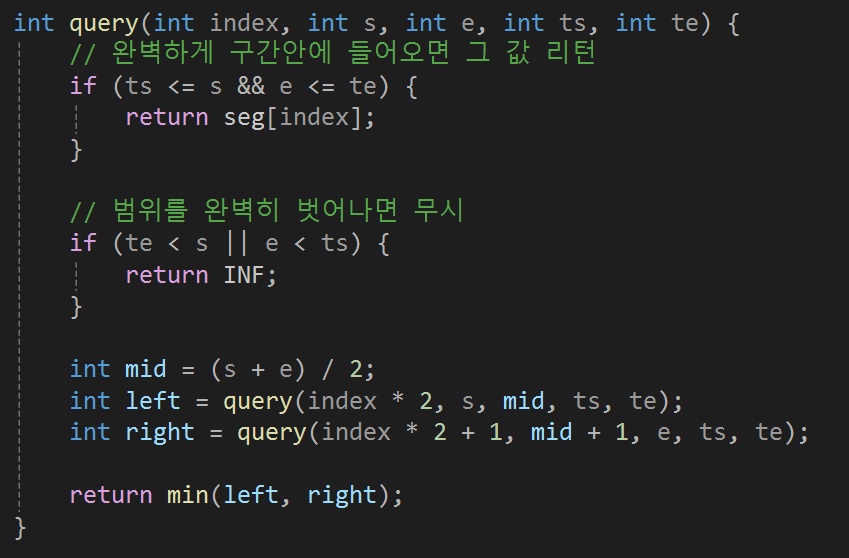
- 범위를 완벽히 벗어나면 min 연산에서 무시되도록 매우 큰 값(=INF)을 정해 리턴하도록 했습니다.
3. Update
Update는 세그먼트 트리를 쓰는 가장 큰 이유입니다. 왜냐하면 Update 후에도 빠른 검색이 가능하기 때문입니다.
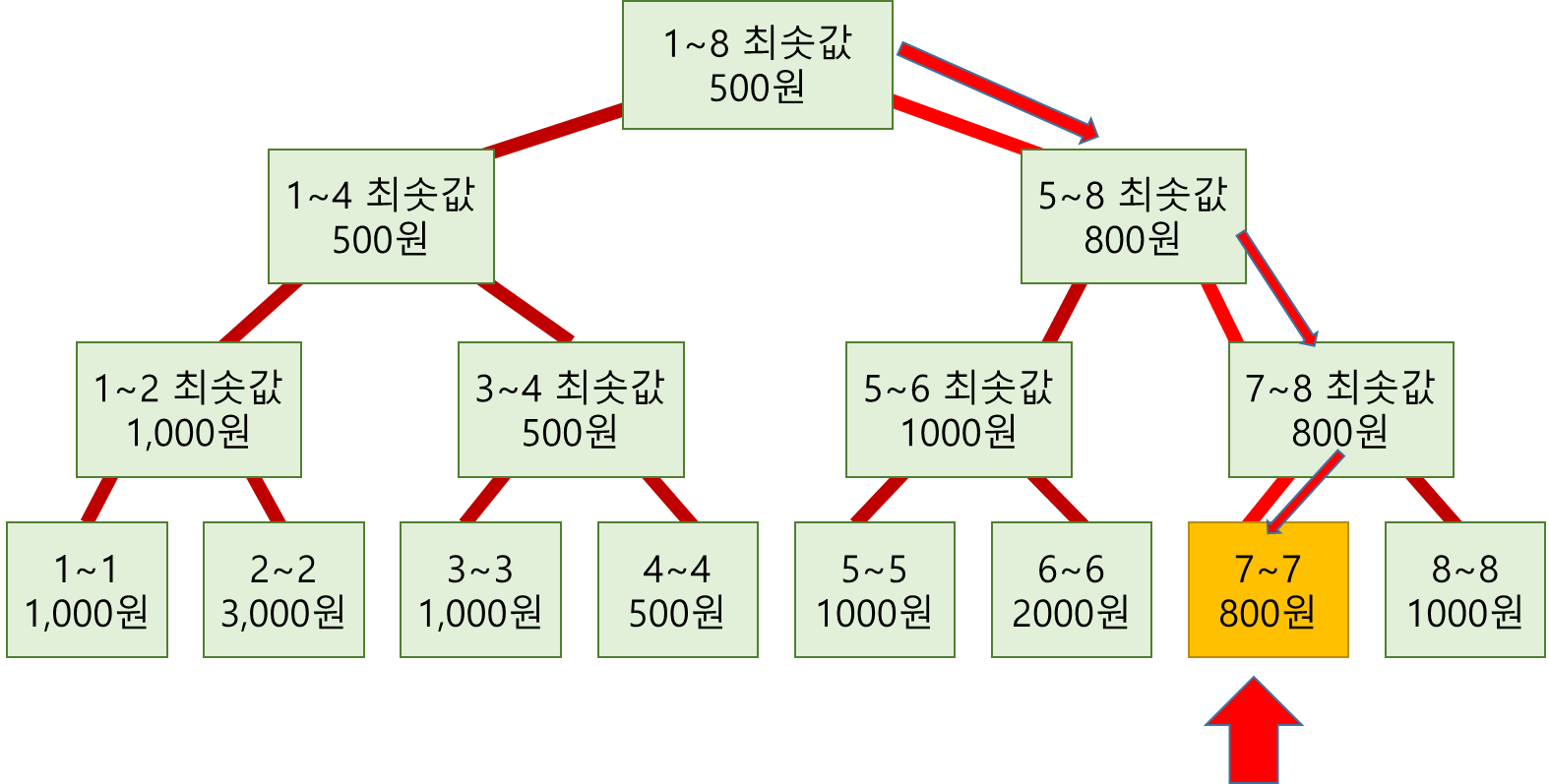
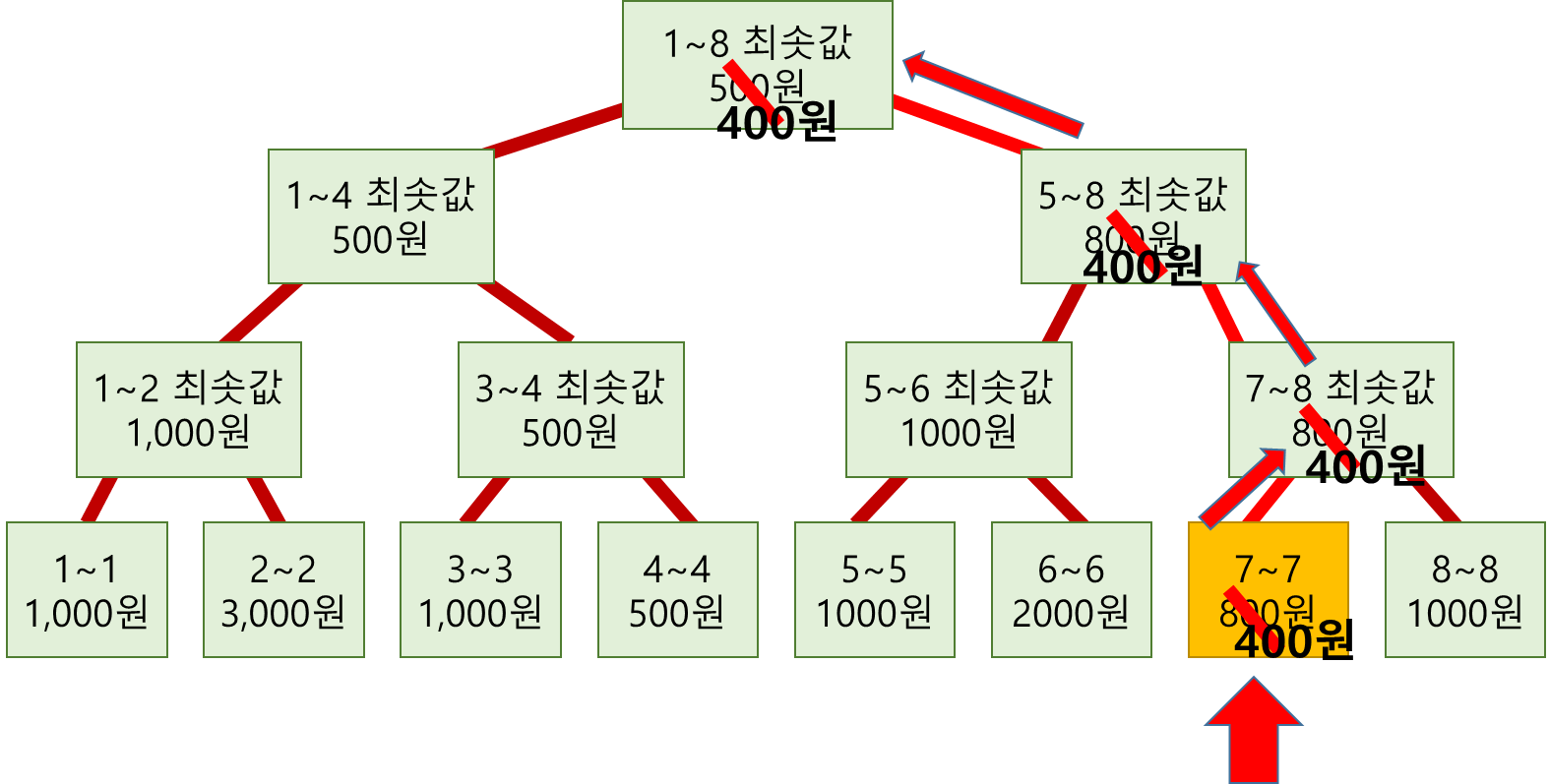
위 세그먼트 트리에서 7을 수정한다고 해보겠습니다. 범위를 절반씩 줄이면서 7을 찾습니다. 그리고 수정합니다. 재귀적으로 7을 찾으면, 콜 스택(Call Stack)이 반환되면서 부모 노드를 순서대로 방문하게 됩니다.
이때 부모노드의 최솟값을 차례대로 업데이트하면, 원래 배열 값이 업데이트 되어도 세그먼트 트리에 으로 반영 가능합니다.
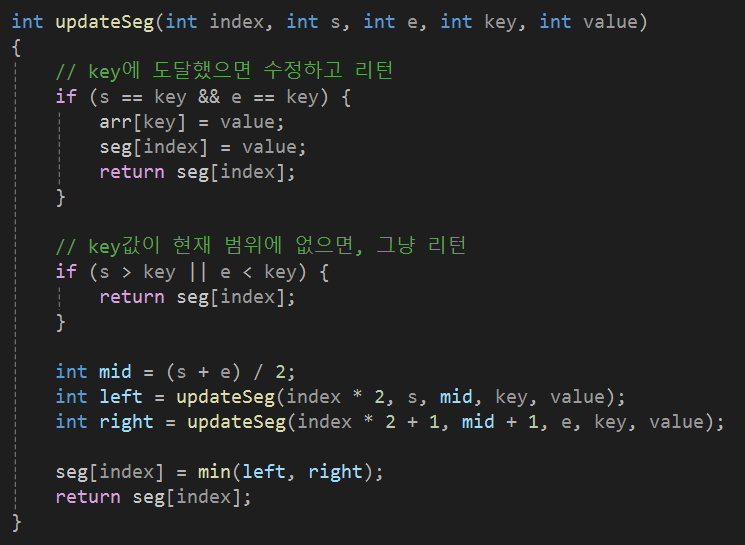
구현 코드:
전체 코드
#include <iostream>
using namespace std;
const int INF = 1e9;
int arr[] = { -9999, 1000, 3000, 1000, 500, 1000, 2000, 800, 1000 };
int seg[30];
int makeSeg(int index, int s, int e);
int query(int index, int s, int e, int ts, int te);
int updateSeg(int index, int s, int e, int key, int value);
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
makeSeg(1, 1, 8);
cout << "query 4-8: " << query(1, 1, 8, 4, 8) << '\n';
cout << "query 3-7: " << query(1, 1, 8, 3, 7) << '\n';
cout << "query 2-7: " << query(1, 1, 8, 2, 7) << '\n';
cout << "query 1-6: " << query(1, 1, 8, 1, 6) << '\n';
updateSeg(1, 1, 8, 7, 400);
return 0;
}
int makeSeg(int index, int s, int e) {
//base
if (s == e) {
seg[index] = arr[s];
return seg[index];
}
int mid = (s + e) / 2;
int left = makeSeg(index * 2, s, mid);
int right = makeSeg(index * 2 + 1, mid + 1, e);
seg[index] = min(left, right);
return seg[index];
}
int query(int index, int s, int e, int ts, int te) {
// 완벽하게 구간안에 들어오면 그 값 리턴
if (ts <= s && e <= te) {
return seg[index];
}
// 범위를 완벽히 벗어나면 무시
if (te < s || e < ts) {
return INF;
}
int mid = (s + e) / 2;
int left = query(index * 2, s, mid, ts, te);
int right = query(index * 2 + 1, mid + 1, e, ts, te);
return min(left, right);
}
int updateSeg(int index, int s, int e, int key, int value) {
if (s == key && e == key) {
arr[key] = value;
seg[index] = value;
return seg[index];
}
if (s > key || e < key) {
return seg[index];
}
int mid = (s + e) / 2;
int left = updateSeg(index * 2, s, mid, key, value);
int right = updateSeg(index * 2 + 1, mid + 1, e, key, value);
seg[index] = min(left, right);
return seg[index];
}Segment Tree 구현 : 구간의 합
세그먼트 트리는 구간의 정보를 저장하는 자료구조라고 했습니다. 이번에는 구간의 합의 정보를 갖고 있는 세그먼트 트리에 대해 알아봅시다. 사실 최솟값 세그먼트 트리와 크게 다르지 않습니다.
1. Construction
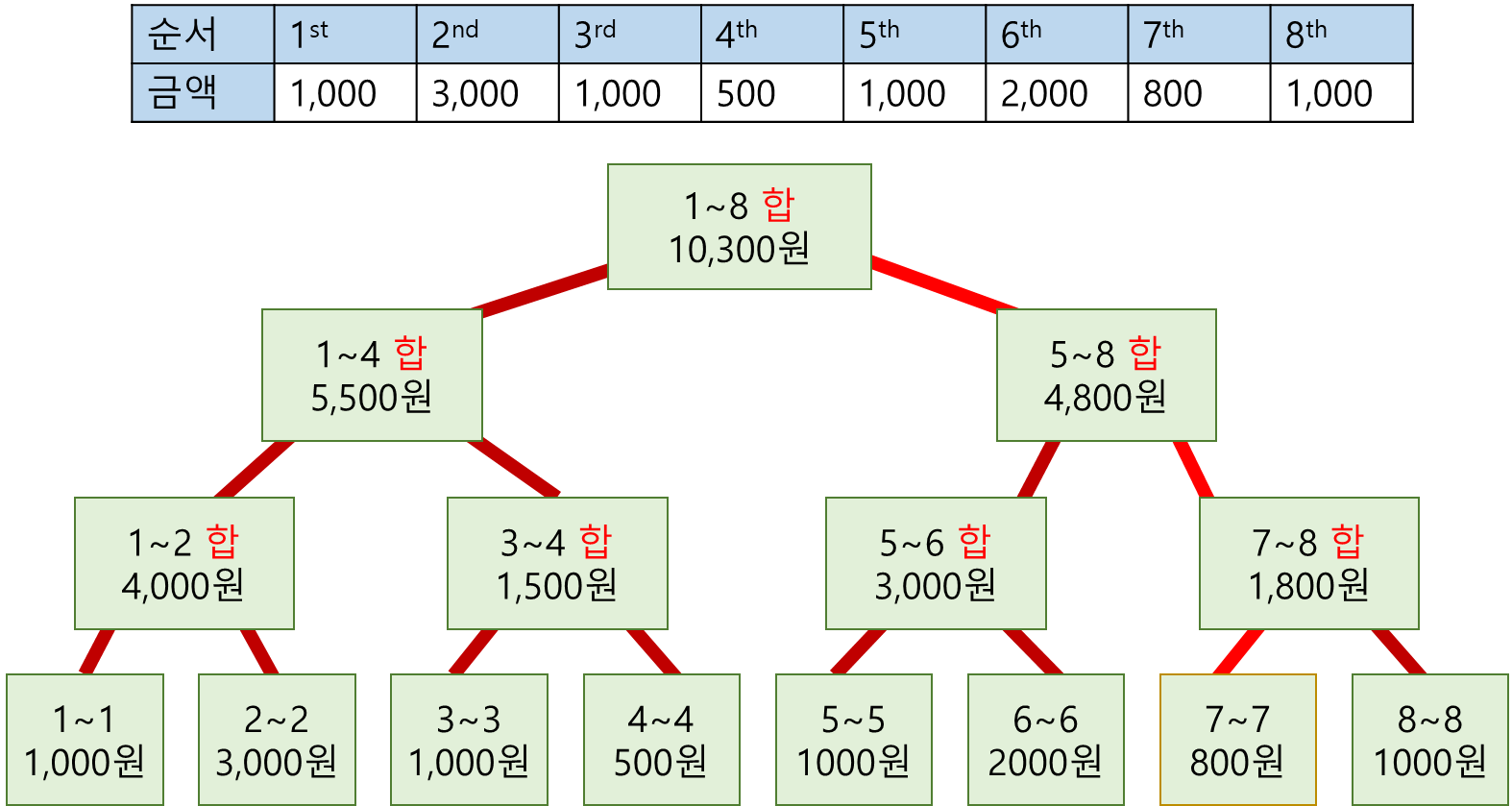
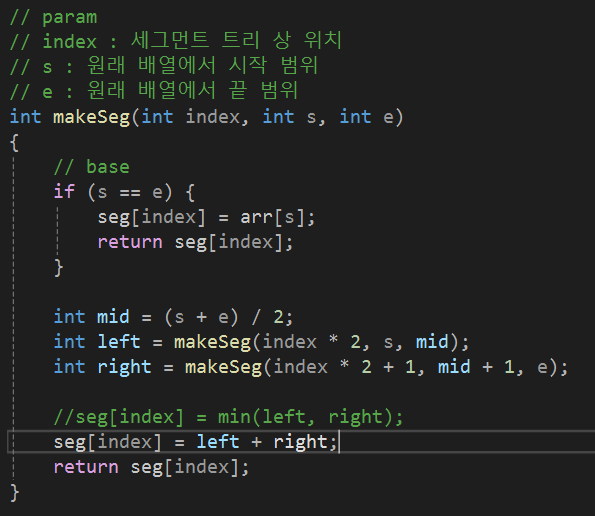
2. Query
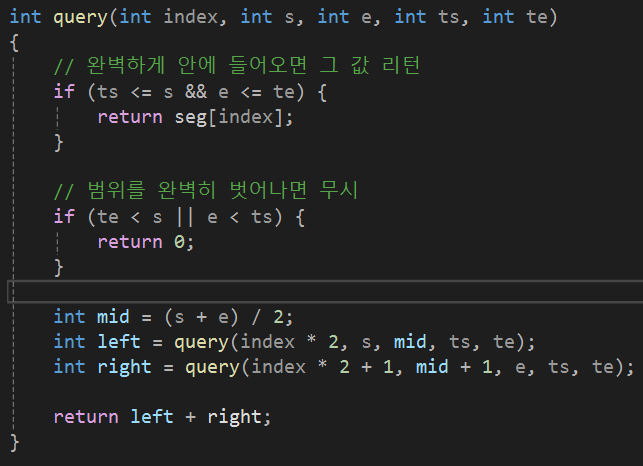
3. Update
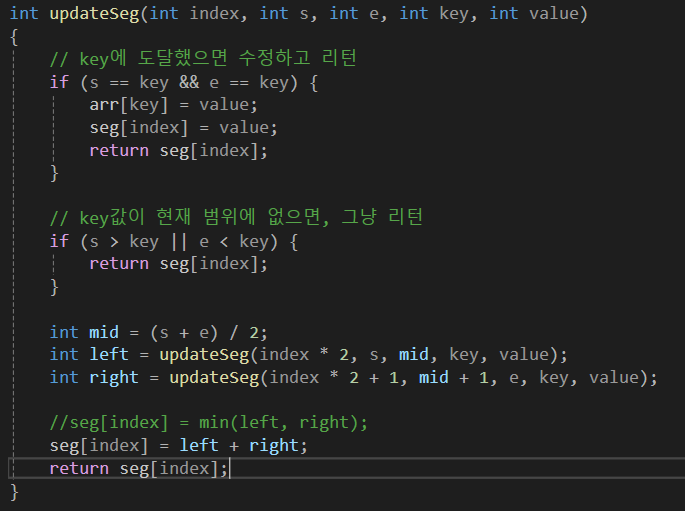
마무리
Segment Tree의 기본 개념과 원리를 바탕으로 최솟값 세그먼트 트리와 구간합 세그먼트 트리의 구현을 살펴보았습니다. 세그먼트 트리의 핵심은 어떤 값이 update 되어도 query 연산이 변함없이 으로 빠르게 수행할 수 있다는 것입니다.
