다익스트라(Dijkstra) 알고리즘
다익스트라 알고리즘은 시작 정점에서 거리가 최소인 정점부터 선택해 나가면서 최단 경로를 구하는 방식으로 동작하는 알고리즘입니다.
>다익스트라 알고리즘은 그리디 알고리즘이다
다익스트라 알고리즘은 현재 정점에서 다음 정점으로 이동할 때, 매번 최소 비용의 간선을 선택하여 이동한다는 점에서 그리디 알고리즘의 한 유형으로 볼 수 있습니다.
>Dijkstra 동작 과정
다익스트라 알고리즘은 다음과 같이 동작합니다.
- 출발 정점을 설정한다.
- 최단 거리 테이블에서 출발 정점을 제외한 다른 정점들을 무한대(매우 큰 값)로 초기화한다.
- 방문하지 않은 노드 중에서 최단 거리가 가장 짧은 정점을 선택한다.
- 정점의 인접 노드로 가는 비용을 계산해 최단 거리 테이블을 갱신한다.
- 위 과정에서
3과4번을 반복한다.
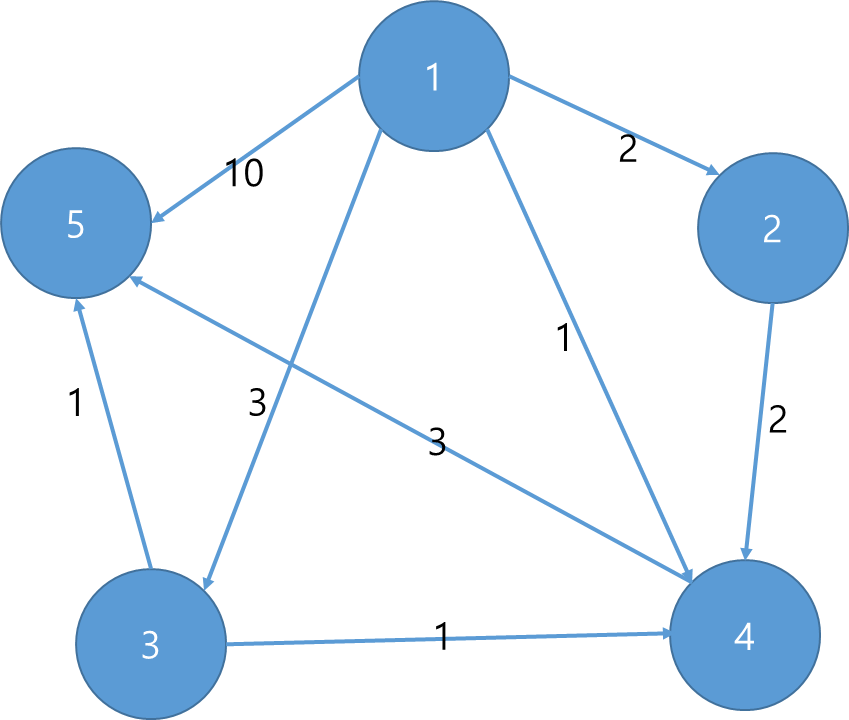
출발 노드는 1이며 최단 거리 테이블을 초기화합니다.
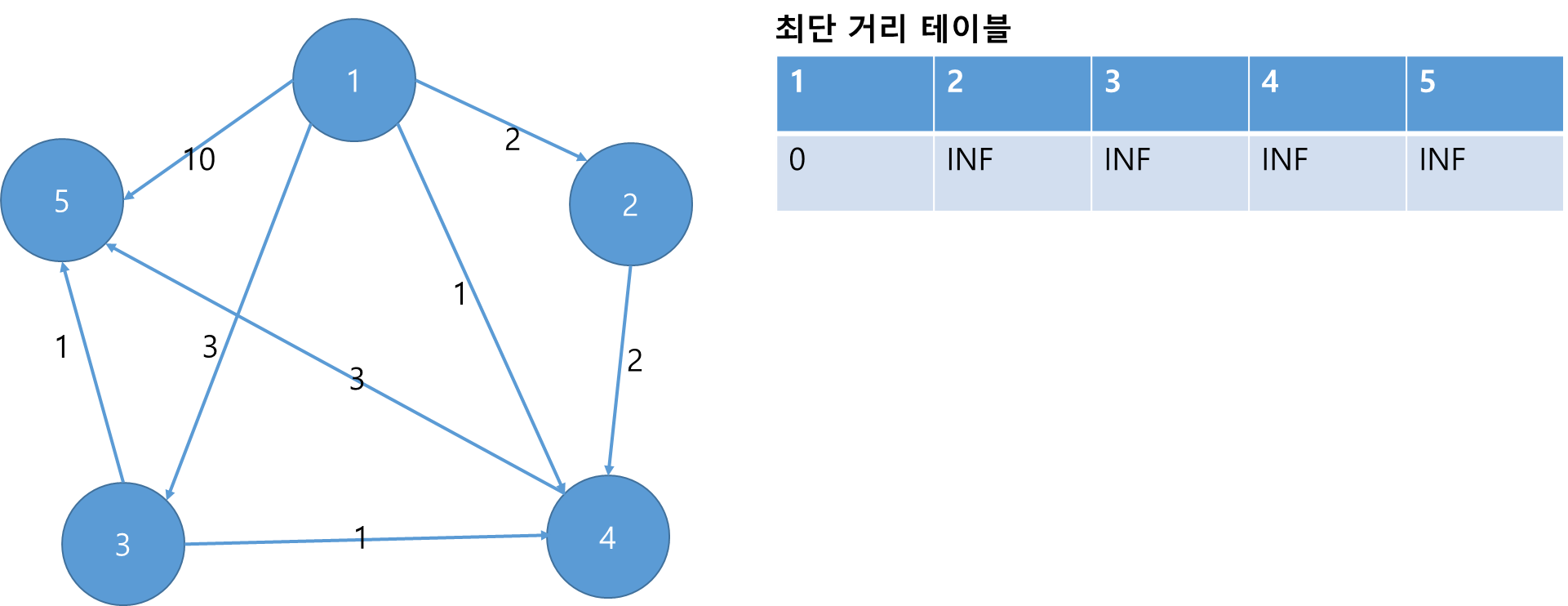
이제 방문하지 않은 정점 중에서 최단 거리가 가장 짧은 정점을 선택합니다. 현재 시작 노드인 1이 가장 작은 값을 가지므로, 1의 인접 노드로 가는 비용을 계산하고 최단 거리 테이블을 갱신합니다.
이때, 1을 방문처리 해줍니다. 방문 처리는 최단 거리가 확정되었다는 뜻입니다.
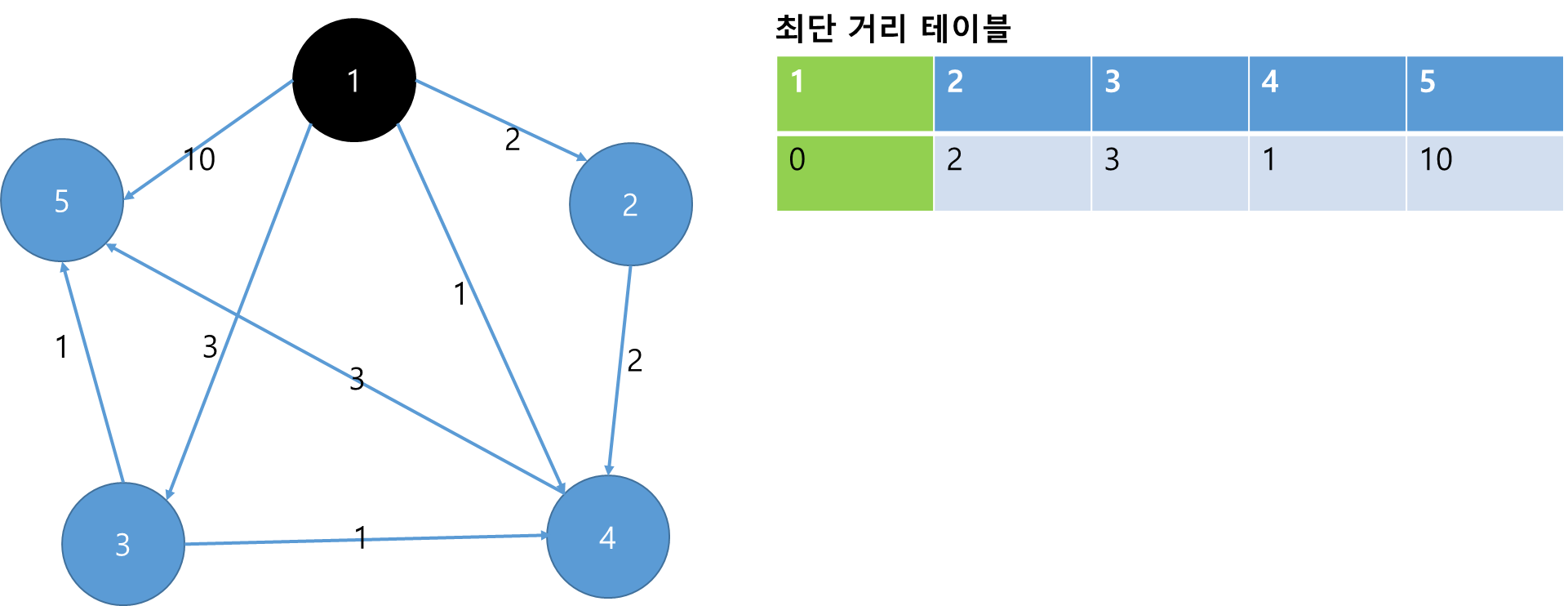
아래부터는 3번과 4번 과정의 반복입니다.
현재 방문하지 않은 노드 중에서 최단거리가 가장 짧은 노드는 4번입니다. 4번을 방문 처리하고, 4번에서 다른 노드로 가는 비용을 계산해서 테이블을 갱신합니다.
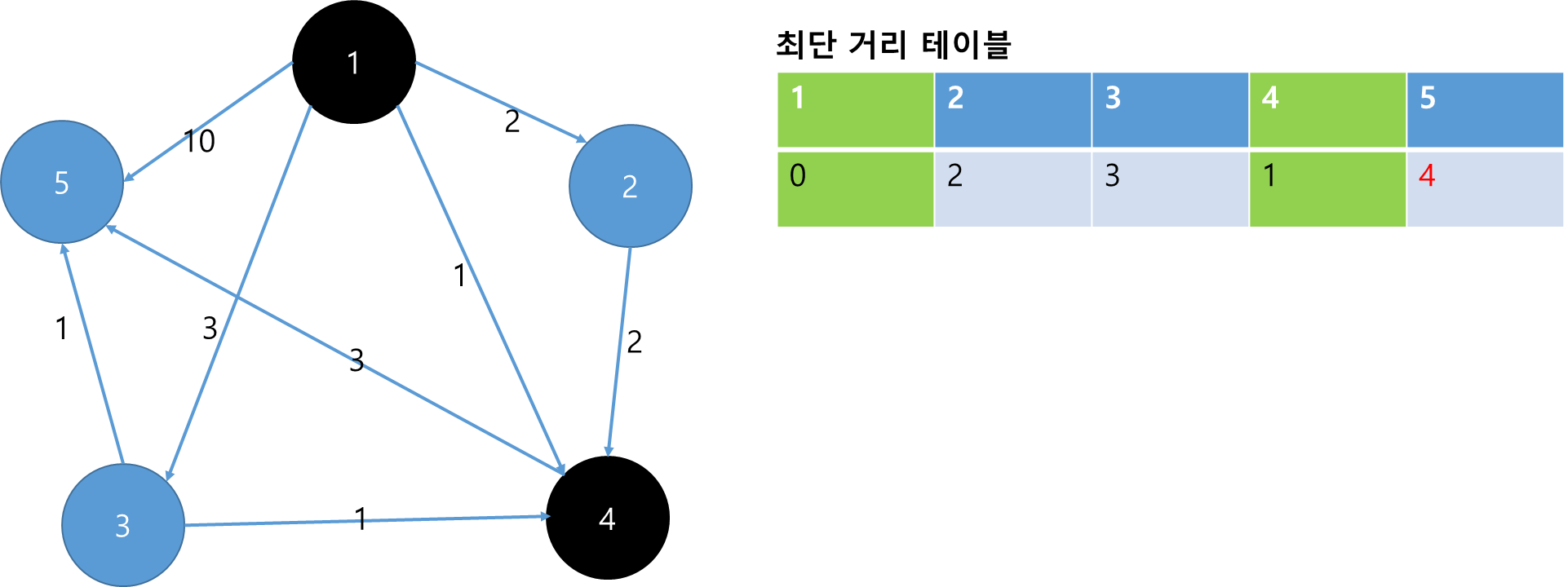
1 -> 5는 10이고 1->4->5는 4이므로 최단 거리 테이블을 갱신합니다.
현재 방문하지 않은 노드 중에서 최단거리가 가장 짧은 노드는 2번입니다. 2번을 방문처리하고, 2번에서 다른 노드로 가는 비용을 계산해서 테이블을 갱신합니다.
위 과정을 반복하면 다음의 최단 거리 테이블이 확정됩니다.
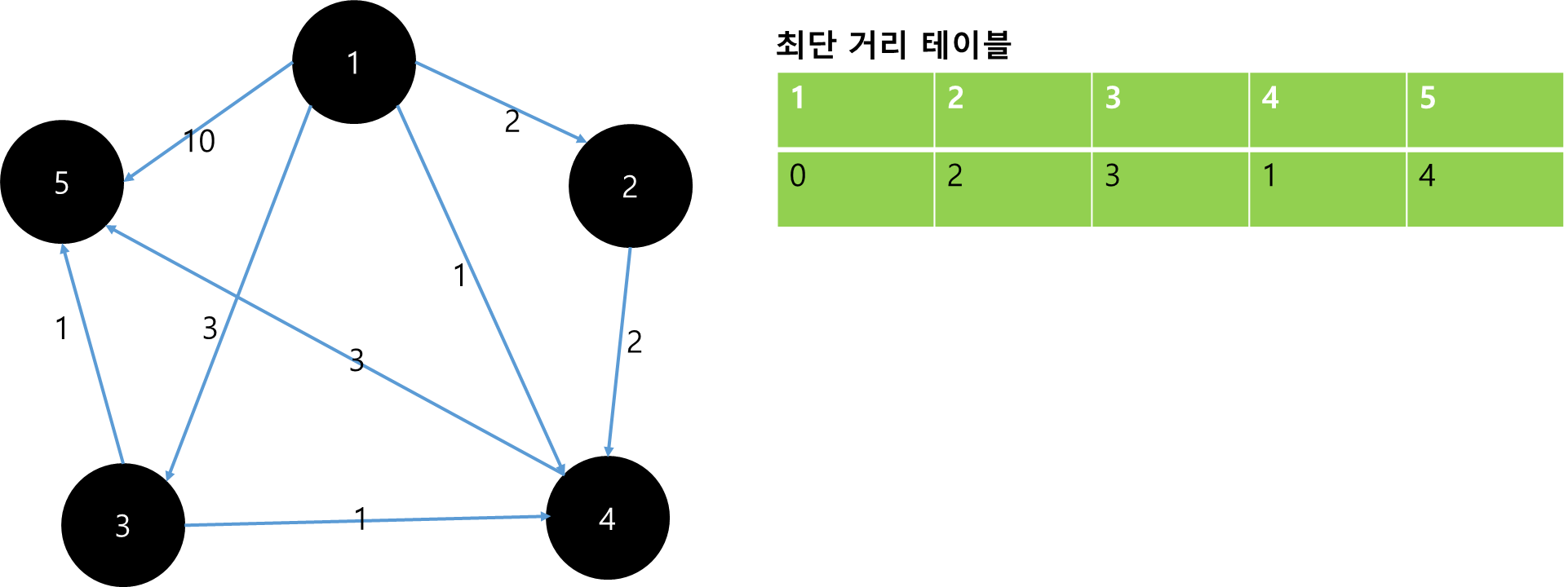
출발지에서 최단거리에 있는 노드는 4이며, 출발점에서 모든 정점으로의 최단거리가 구해졌습니다.
구현을 위한 Dijkstra
아래 설명은 백준 1916. 최소비용 구하기를 기준으로 작성되었습니다.
이제 코드로 구현하는 방법을 살펴보겠습니다.
먼저 정점끼리의 관계를 나타내는 그래프 자료구조가 필요합니다. 또한 최단 거리 테이블과 방문 여부를 알기 위한 테이블이 필요합니다.
struct Node
{
int num;
int cost;
};
vector<Node> graph[1001];
int visited[1001];
int dist[1001];
int N, M;
int startNum, endNum;그래프를 표현하기 위해 인접 리스트 방식을 활용하였습니다.
이제 Input() 함수로 입력을 받고 dist 테이블을 초기화합니다.
void Input()
{
cin >> N >> M;
int from, to, cost;
for (int i = 0; i < M; i++)
{
cin >> from >> to >> cost;
graph[from].push_back({ to, cost });
}
for (int i = 1; i <= N; i++)
{
dist[i] = 1e9;
}
cin >> startNum >> endNum;
}다익스트라 함수는 시작 노드를 방문처리하고, 최단거리 테이블을 갱신하며 시작됩니다
visited[startNum] = true;
dist[startNum] = 0;
// 같은 목적지로 가는 여러 개의 노드가 있는 경우를 대비
for (int i = 0; i < graph[startNum].size(); i++)
{
if(dist[graph[startNum][i].num] > graph[startNum][i].cost)
dist[graph[startNum][i].num] = graph[startNum][i].cost;
}다익스트라는 문제의 크기가 N이라면 N번의 탐색 이후 종료됩니다. N번의 탐색 안에, 최단거리 노드를 찾는 과정과 최단 거리 테이블을 갱신하는 과정이 있습니다.
void Dijkstra()
{
visited[startNum] = true;
dist[startNum] = 0;
for (int i = 0; i < graph[startNum].size(); i++)
dist[graph[startNum][i].num] = graph[startNum][i].cost;
int now, cost;
for (int i = 1; i < N; i++)
{
now = GetSmallestNode();
visited[now] = true;
for (int j = 0; j < graph[now].size(); j++)
{
cost = dist[now] + graph[now][j].cost;
if (dist[graph[now][j].num] > cost)
dist[graph[now][j].num] = cost;
}
}
}
int GetSmallestNode()
{
int minVal = 1e9;
int rst = -1;
for (int i = 1; i <= N; i++)
{
if (visited[i])
continue;
if (dist[i] < minVal)
{
rst = i;
minVal = dist[i];
}
}
return rst;
}개선된 다익스트라 알고리즘
앞서 구현한 다익스트라는 최단 거리 노드를 노드 개수만큼 선형적으로 탐색하여 의 시간복잡도를 갖습니다. 시간복잡도를 줄이기 위해, 개선된 다익스트라 알고리즘이 존재합니다.
이는 힙(heap)으로 구현된 우선순위 큐(priority queue)를 사용하여, 우선 순위에 따라 정렬된 큐를 만들면 시간복잡도를 줄일 수 있습니다.
거리가 작은 순서대로 정렬되는 큐를 선언하고, 이 큐에 다음 노드와 현재 노드에서 다음 노드로 가는 거리를 넣습니다.
#include <iostream>
#include <queue>
#include <vector>
using namespace std;
struct Node
{
int n;
int price;
bool operator<(const Node& other) const{
return other.price < price;
}
};
vector<Node> alist[1001];
priority_queue<Node> pq;
int best[1001];
int N, M;
int startNum, endNum;
void Input();
void Dijkstra();
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
Input();
Dijkstra();
cout << best[endNum] << '\n';
return 0;
}
void Input()
{
cin >> N >> M;
int from, to, cost;
for(int i=0; i<M; i++)
{
cin>>from>>to>>cost;
alist[from].push_back({to, cost});
}
for(int i=1; i<=N; i++)
{
best[i] = (int)1e9;
}
cin >> startNum >> endNum;
}
void Dijkstra()
{
best[startNum] = 0;
pq.push({startNum, 0});
Node now;
while(!pq.empty())
{
now = pq.top(); pq.pop();
//dummy가 아닌 경우만
if(now.price <= best[now.n])
{
for(Node next : alist[now.n])
{
if(best[next.n] > now.price + next.price)
{
best[next.n] = now.price + next.price;
pq.push({next.n, best[next.n]});
}
}
}
}
}
