1. What is Recursion? 🧐
리스트에 있는 수 다 더하기 ➕
두 수를 더하는 방법은 너무나 쉽습니다. 여러 개의 수를 더하는 것도 쉽죠. 라는 수열을 다 더하라고 하면, 우리는 그냥 다 더합니다. 더 말할 필요도 없죠. 그런데, 수학적으로는 '두 개의 수를 더해서, 그 결과를 다음의 수와 더하라'는 약속이 있습니다. 이를 표현하면 다음과 같습니다.
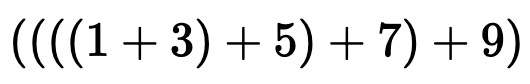
그런데 이렇게도 표현할 수 있습니다.
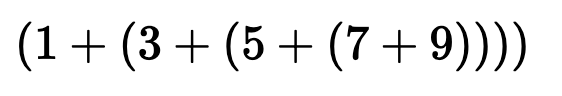
이렇게 수열(리스트)을 입력하면 합을 출력하는 함수를 프로그래밍하려면 어떻게 해야 할까요? 일단 두 개의 수를 더해야 한다는 약속에 따라야 합니다. 프로그래밍으로는 두 개의 수를 더하는 이항 연산밖에 할 수 없기 때문입니다. 결국, '리스트를 입력하면 합을 출력하는 함수가 있다'고 믿는 것입니다.(?) 🙏
믿음의 영역 ✨

위 그림을 볼까요? 리스트를 입력하면 합을 출력하는 함수가 있다면, 표시된 sub-list도 합을 출력해 줄 것입니다. 이 함수를 listsum()이라고 하겠습니다. 그러면 1과 listsum(sublist)가 리턴하는 값을 A + B로 나타낼 수 있으므로, 정답을 출력할 수 있습니다.

이렇게 표현할 수 있습니다. 그런데, listsum(list[1:])가 리턴하는 값을 알아볼까요?

이때에도 listsum은 바로 정답을 구할 수는 없고, 3과 listsum이 리턴하는 값으로 A + B해야만 합니다. listsum은 언제 값을 리턴할 수 있을까요? 아래 그림은 listsum이 값을 리턴할 수 있는 지점까지의 과정입니다.
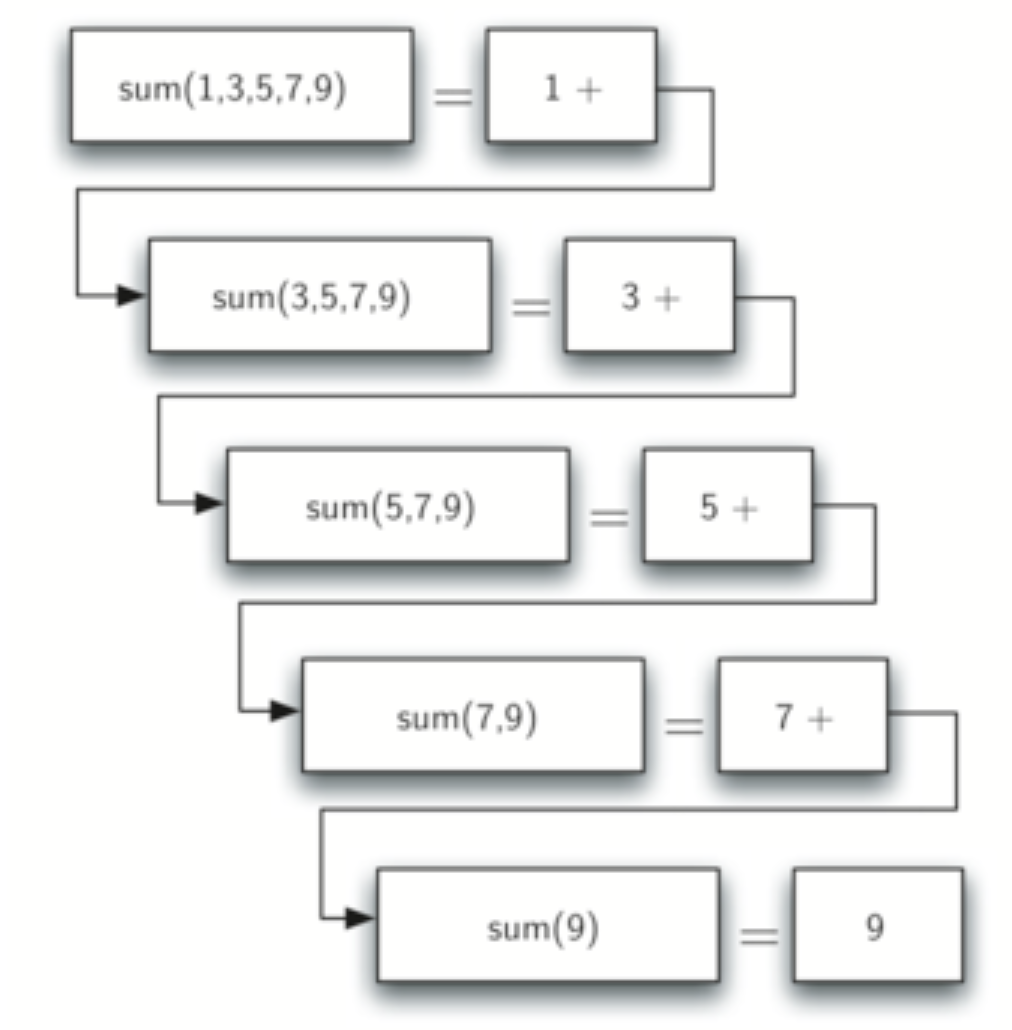
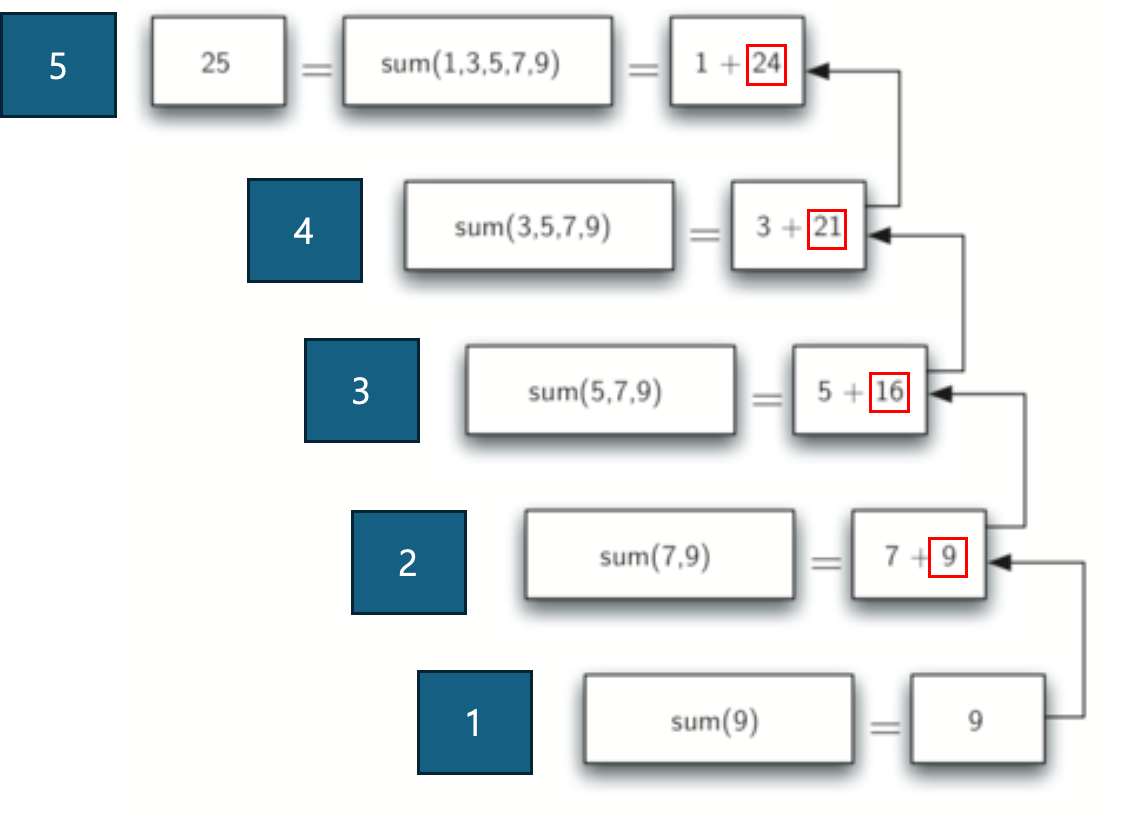
리스트에 수가 하나밖에 없다면, 더이상 A + B 형태로 쪼갤 수 없습니다. 그래서 listsum을 호출할 수 없고, 리스트에 있는 수를 그냥 리턴해야 합니다. 이렇게 리턴이 시작되면, 앞에서 호출했던 모든 listsum이 값을 갖게 되고, A + B 할 수 있습니다. 그 과정을 순서대로 나타낸 그림은 아래와 같습니다.
정리 📝
정리를 하자면,
어떤 수열(리스트)을 더하는 함수가 있다. 그래서 나는 그 함수에 리스트를 입력했다. 그런데 숫자를 더하려면 A + B 해야 하니까, 수열의 맨 처음 애랑 그 뒤에
sub-list를 함수에 대입하여 더하게 했다. 근데 생각해보니까sub-list를 구할때에도 똑같은 과정을 거쳐야 한다. 그럼 언제 이 함수는 리턴할 수 있을까. 리스트에 숫자가 하나밖에 없으면 A + B 못하니까 그냥 그 숫자를 리턴하자. 🎯
입니다. 파이썬 코드로 작성하면 다음과 같습니다.
def listsum(list):
if len(list) == 1:
return list[0]
else:
return list[0] + listsum(list[1:])
print(listsum([1,3,5,7,9])2. Three Laws of Recursion 📜
앞선 예제를 통해서도 예상해볼 수 있겠지만, 재귀함수를 작성할 때는 세 가지 규칙을 지켜야합니다.
1. 기저 조건(base case)을 가져라 🛑
2. 기저 조건으로 이동하며 상태를 바꿔라 ↘️
3. 자기 자신을 호출하라 🔁
Law 1. 기저 조건을 가져라. 🛑
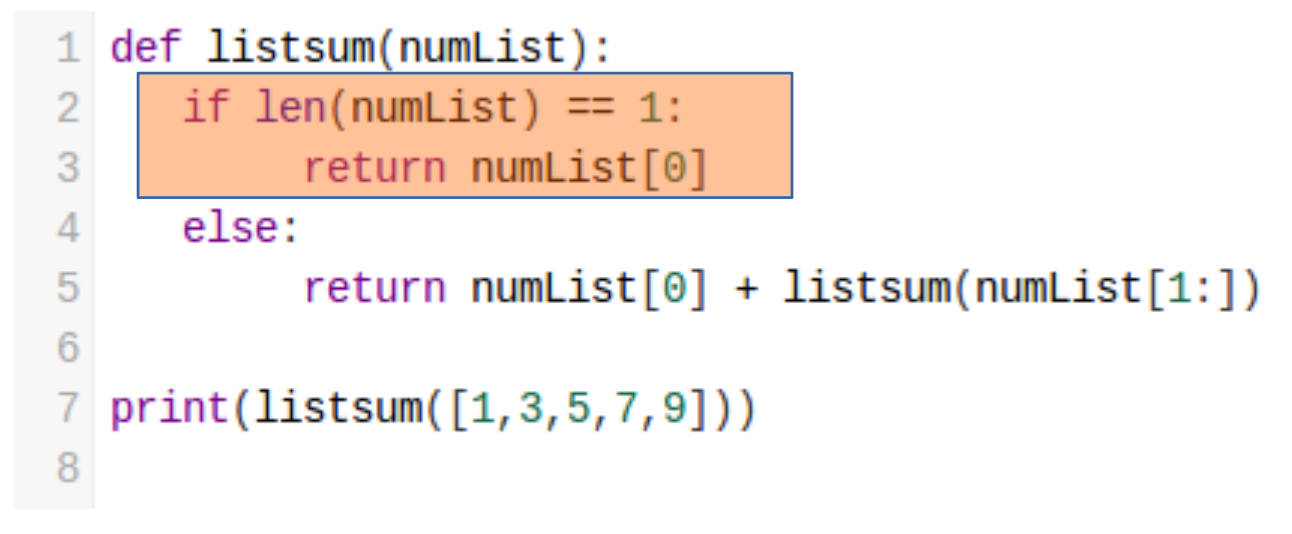
base case는 sub-problem이 충분히 작아 재귀가 끝날 때의 조건을 뜻합니다.
앞선 예시에서 기저 조건 바로 리스트의 길이가 1이될 때입니다.
Law 2. 기저 조건으로 이동하며 상태를 바꿔라 ↘️
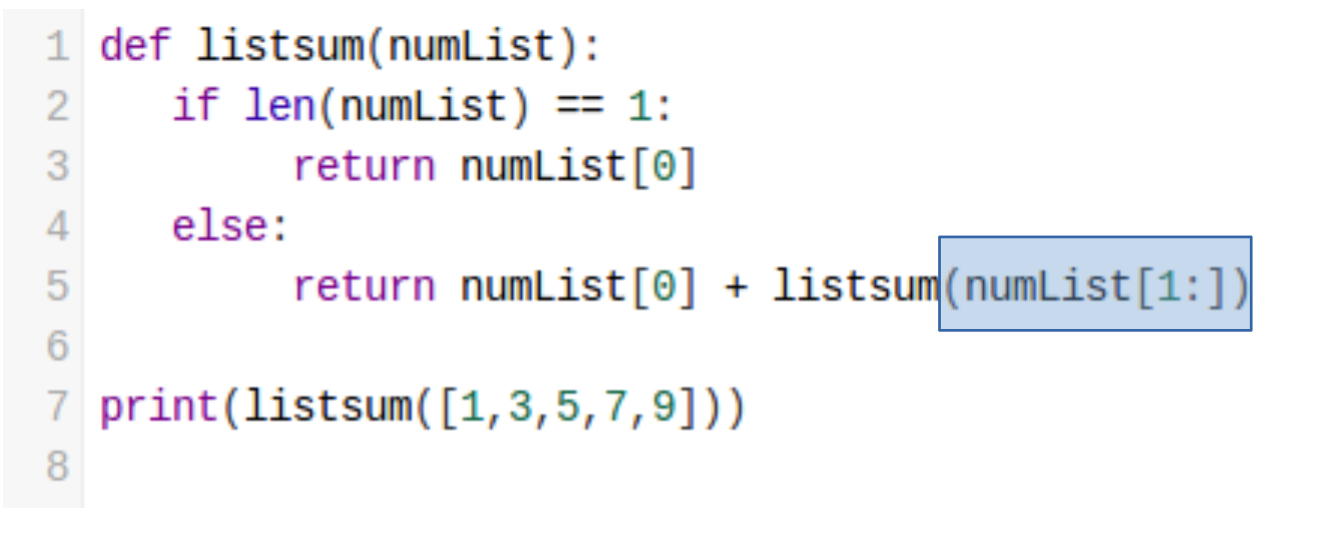
state change는 data가 계속 작아지는 것을 뜻합니다.
앞선 예시에서는 리스트의 길이가 계속해서 작아지는 것입니다.
Law 3. 자기 자신을 호출하라 🔁
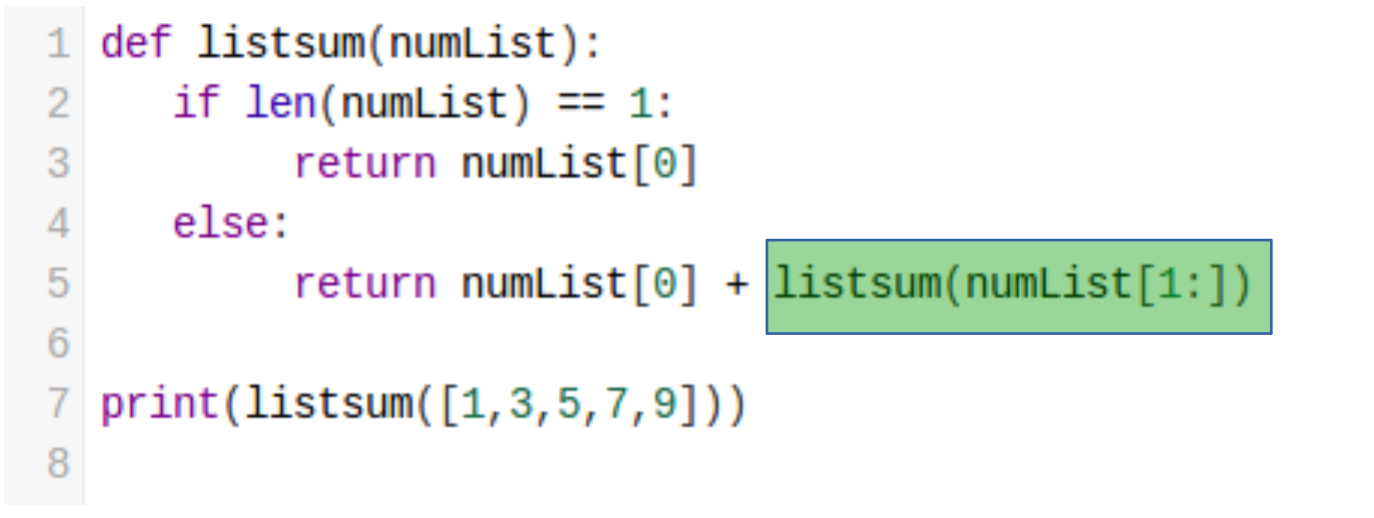
3. Pros and Cons of Recursion ⚖️
피보나치 수열 🌱
피보나치 수는 를 만족하는 수입니다. 이를 프로그래밍하면 다음과 같습니다.

굉장히 직관적이고 단순하지 않나요? 😊
이 함수가 어떻게 동작하는지 fib(5)에 대한 function call을 그려보면 다음과 같습니다.
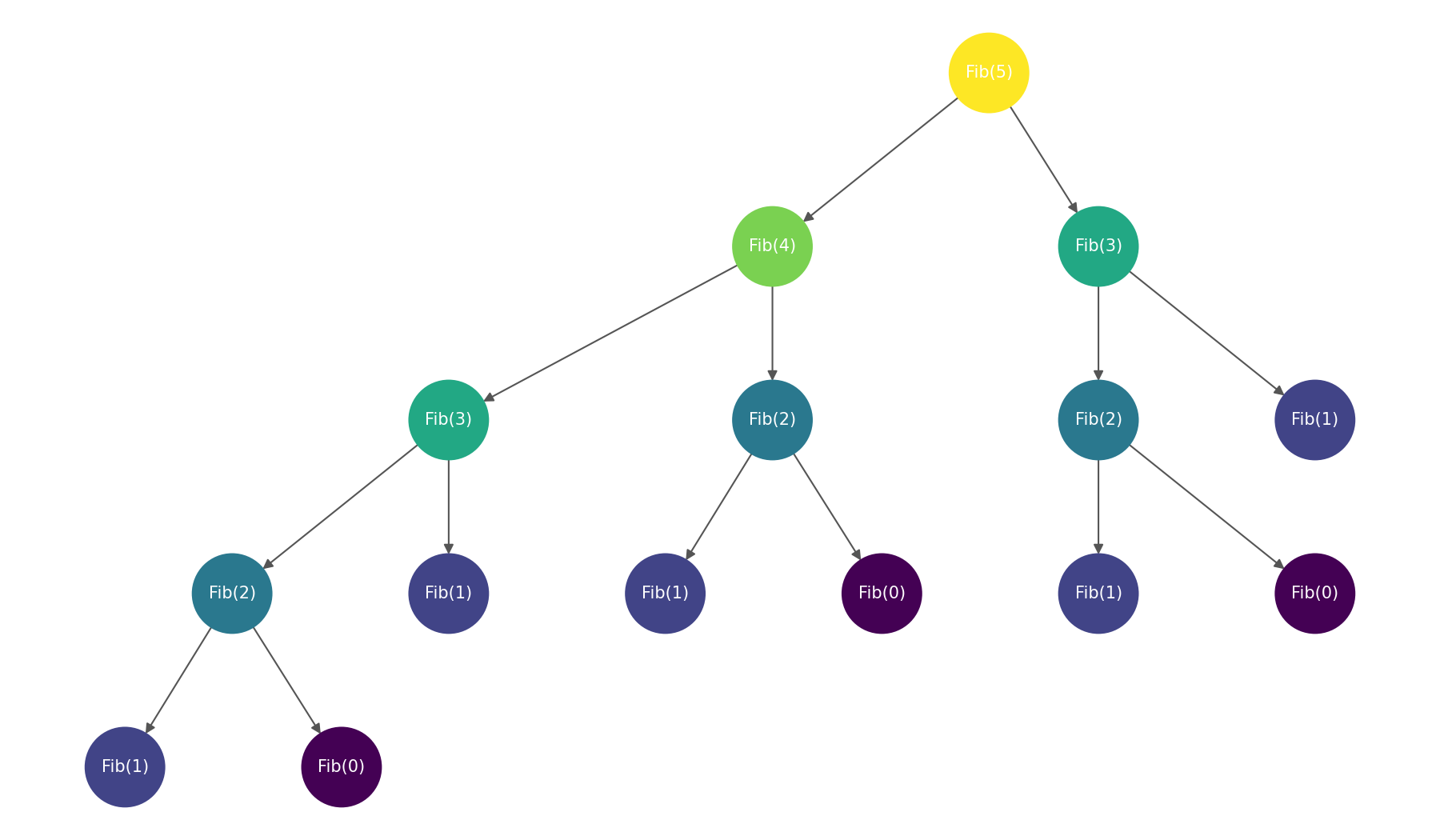
이미 한 번 호출한 경우를 다시 호출하여 중복된 호출이 일어나고 있습니다. 이처럼 재귀에는 장점과 단점이 명확합니다.
| ✅ 장점 | ⚠️ 단점 |
|---|---|
| • 간결한 코드 ✂️ • 직관적이고 이해하기 쉬움 👀 | • stacking으로 인한 추가 메모리 소비 💾• 잘못 설계 시 느린 실행 🐢 |
이때
stacking은 재귀 호출을 위해function call을 스택처럼 메모리 공간에 쌓아놓는 것을 뜻합니다. 예를 들어, fib(5)를 구하기 위해 fib(4)로 들어가는 순간, 현재 상태를 저장하고 들어가야 합니다. 그래야 재귀 호출이 종료되고 돌아왔을 때 리턴된 값을 현재 상태의 값과 연산할 수 있습니다.
4. 마무리 🎬
재귀(Recursion)는 “자기 자신을 정의로 사용해 문제를 풀어가는 사고방식”입니다.
-
Three Laws를 지키면:
1. 기저 조건(Base Case)으로 끝맺고,
2. 그쪽으로 점진적 이동(State Change)을 하며,
3. 자신을 다시 호출해 구조를 반복합니다. -
이 덕분에 코드를 짧고 직관적으로 만들 수 있지만,
- 호출 스택이 쌓이면서 메모리/성능 비용이 뒤따를 수 있고,
- 잘못 설계하면 중복 계산으로 느려질 수 있습니다.
결국 “가독성 vs 성능”의 균형이 관건입니다.
-
트리·그래프 탐색, 분할정복처럼 문제 구조가 재귀적이면 과감히 쓰고,
-
단순 누산·반복만 필요한 곳에선 반복문이 더 깔끔할 수 있습니다.
