
1. Introduction
Searching
데이터를 찾는다는 것은 프로그래밍에서 굉장히 중요한 작업입니다. 데이터가 저장된 테이블에서 원하는 값을 찾는 방법에는 여러 가지가 있습니다.

가장 단순한 방법은 순차 탐색(Sequential Search)입니다. 데이터를 처음부터 끝까지 하나씩 확인하면서 원하는 값을 찾는 방식입니다. 예를 들어, 스마트폰에서 특정 사진을 찾기 위해 갤러리를 처음부터 끝까지 하나씩 넘겨보는 방식과 같습니다. 하지만 이 방법은 최악의 경우 모든 데이터를 확인해야 하므로 시간 복잡도는 입니다.
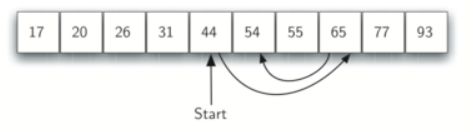
좀 더 빠른 방법으로는 이진 탐색(Binary Search)이 있습니다. 정렬된 데이터에서 중앙값을 기준으로 절반씩 줄여가며 탐색하는 방식입니다. 예를 들어, 사전에서 특정 단어를 찾을 때 무작정 첫 페이지부터 넘기는 것이 아니라, 중간 페이지를 펼쳐 단어가 앞쪽에 있는지 뒤쪽에 있는지를 판단한 후 해당 범위에서 다시 중간을 찾는 방식과 같습니다. 이렇게 하면 탐색 속도가 대폭 향상되어 시간 복잡도가 이 됩니다. 하지만 이진 탐색을 사용하려면 데이터가 정렬되어 있어야 한다는 전제 조건이 필요합니다.
Hashing
그렇다면 더 빠르게 찾을 수 있는 방법은 없을까요? 해싱(Hashing)이 바로 그 해결책입니다.
해싱을 이용하면 데이터 검색을 평균적으로 의 시간 복잡도로 수행할 수 있습니다. 즉, 데이터의 크기에 관계없이 거의 즉각적으로 원하는 값을 찾을 수 있습니다. 예를 들어, 편의점에서 원하는 상품을 찾을 때, 매장을 돌아다니며 하나씩 확인하는 대신, 직원에게 위치를 물어보고 바로 해당 진열대로 가는 것과 같은 개념입니다. 그렇다면 해싱은 어떻게 빠른 탐색이 가능할까요?
2. Hashing
Hash Table

해싱(hashing)은 해시 테이블(Hash Table)이라는 구조를 기반으로 동작하며, 테이블에는 데이터가 키-값(Key-Value) 쌍으로 저장됩니다. 즉, 특정 키를 사용하여 해당 값을 빠르게 찾을 수 있도록 매핑하는 방식입니다.
Hash Function
그렇다면 어떻게 키를 이용해 값을 찾을 수 있을까요? 바로 해시 함수(Hash Function)가 그 역할을 합니다. 해시 함수는 입력된 값을 특정한 값(해시 값)으로 변환하여, 해당 값을 기반으로 저장된 위치를 빠르게 찾아낼 수 있도록 합니다.
이 방식 덕분에 해싱은 대부분의 경우 평균적으로 의 시간 복잡도로 데이터를 검색할 수 있습니다.

예를 들어, 해시 테이블의 크기가 11이라고 가정해 보겠습니다. 여기에 54, 26, 93, 17, 77, 31을 넣는다고 해봅시다. 이들의 위치를 정하기 위해 어떤 해시 함수를 사용하면 좋을까요?

가장 좋은 방법 중 하나는 나머지 연산(Modulo Operation)을 이용하는 것입니다. 각 키 값을 해시테이블의 크기로 나머지 연산을 수행하면 위 표와 같이 키 값을 0~10 사이의 값으로 변환할 수 있습니다.

Kind of Hash Functions
해시 함수에는 여러 가지 종류가 있으며, 각각 다른 방식으로 키를 해시 값으로 변환합니다. 대표적인 해시 함수의 종류는 다음과 같습니다.
1. Folding Method
키 값을 일정한 크기의 부분으로 나누고, 이 부분들을 더하거나 특정 연산을 수행하여 해시 값을 생성하는 방식입니다.
예를 들어, 키가 123456이라면 12 + 34 + 56 = 102와 같이 부분을 더한 후 필요에 따라 추가적인 연산을 수행할 수 있습니다.
2. Mid-Square Method
키 값을 제곱한 후, 그 중앙 부분을 해시 값으로 사용하는 방법입니다.
예를 들어, 키가 123이라면 123^2 = 15129가 되고, 중앙 숫자 512를 해시 값으로 사용합니다.
3. Hashing for Characters
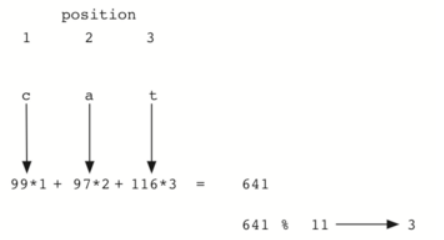
문자열 데이터를 해싱하기 위한 방법으로, 일반적으로 각 문자의 ASCII 값을 조합하여 해시 값을 생성합니다.
예를 들어, 문자열 ABC의 경우 A(65) + B(66) + C(67) = 198과 같은 방식으로 해시 값을 만들 수 있습니다.
Collision

앞선 상황에서 를 추가해봅시다. 해시 함수가 해시 테이블 크기로 나머지 연산을 수행하는 함수라고 할 때, 의 해시 값은 입니다. 그런데 해당 해시 주소에는 값이 이미 존재하는데, 이런 상황을 충돌(Collision)이라고 합니다.
해시 충돌이 발생하면, 같은 해시 값을 가진 여러 개의 키가 동일한 위치에 저장되려고 하면서 데이터의 정확성이 떨어질 수 있습니다. 따라서 충돌을 최소화하는 것이 중요합니다.
Collision Resolution
아무리 좋은 해시 함수를 사용하더라도 충돌(Collision)은 피할 수 없는 문제입니다. 그렇다면 충돌이 발생했을 때 어떻게 해결할 수 있을까요? 이를 Collision Resolution이라고 하며, 몇 가지 주요 방법이 있습니다.
1. Open Addressing (개방 주소법)
충돌이 발생하면 다른 빈 슬롯을 찾아 데이터를 저장하는 방식입니다.
대표적인 기법으로 선형 탐사(Linear Probing), 이차 탐사(Quadratic Probing), 이중 해싱(Double Hashing) 등이 있습니다.
다음은 선형 탐사를 이용해서 77과 같은 해시값을 갖는 55와 44를 해시 테이블에 입력하는 예시입니다.




하지만 이 방법은 클러스터링(Clustering) 문제를 일으킬 수 있습니다.

즉, 동일한 해시 값을 가진 여러 항목이 연속된 슬롯에 저장되면서 특정 영역에 데이터가 집중되게 됩니다. 이로 인해 추가적인 데이터 삽입 시 검색 시간이 길어지고 성능이 저하될 수 있습니다.
2. Quadratic Probing (이차 탐사법)

선형 탐사와 유사하지만, 충돌이 발생할 경우 일정한 간격이 아닌 제곱 간격으로 다음 슬롯을 탐색하는 방식입니다.
예를 들어, 첫 번째 충돌 시 +1, 두 번째 충돌 시 +4, 세 번째 충돌 시 +9 등의 규칙으로 이동합니다.
3. Chaining (체이닝 기법)
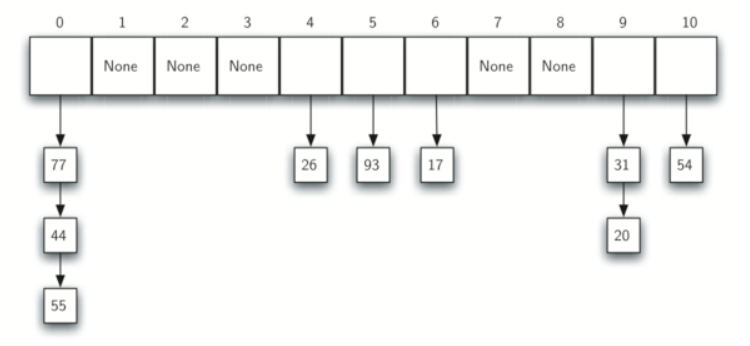
같은 해시 값을 가진 데이터를 연결 리스트(Linked List) 형태로 저장하여 충돌을 해결하는 방식입니다.
이 방법은 테이블 크기에 영향을 덜 받지만, 리스트 탐색 시간이 추가로 필요할 수 있습니다.
마무리
해쉬 자료구조를 활용하면 정수 뿐만 아니라, 문자열을 인덱스로 활용해 데이터에 접근할 수 있습니다. 감사합니다.
