[자료구조 및 알고리즘] Balanced Binary Search Tree

신동욱·2025년 1월 27일

목록 보기

12/18

🌪️ worst case of BST

위 그림처럼, key값이 오름차순 정렬된 순서로 BST를 구성해봅시다. 이 트리는 삽입, 삭제, 탐색이 $O(N)$ 의 시간복잡도를 가지게 됩니다. 어떻게 하면 이진 탐색 트리가 $O(logN)$ 의 시간복잡도를 보장하게 할 수 있을까요?

️🌉 Balancing

아이디어는 간단합니다. 트리의 균형이 깨질 수 있는 삽입 혹은 삭제가 일어날 때마다, 왼쪽 서브 트리(left subtree)와 오른쪽 서브 트리(right subtree)가 같은 깊이(depth)를 갖도록 조정하면 됩니다. 이러한 트리를 AVL 트리라고 합니다. 그럼 구현은 어떻게 해야 할까요?

Balance factor라는 용어로 이를 설명해보겠습니다. Balance factor는 (왼쪽 서브트리의 높이) - (오른쪽 서브트리의 높이)입니다. 그렇다면 Balance factor는 -1 또는 0 또는 1이어야 합니다.

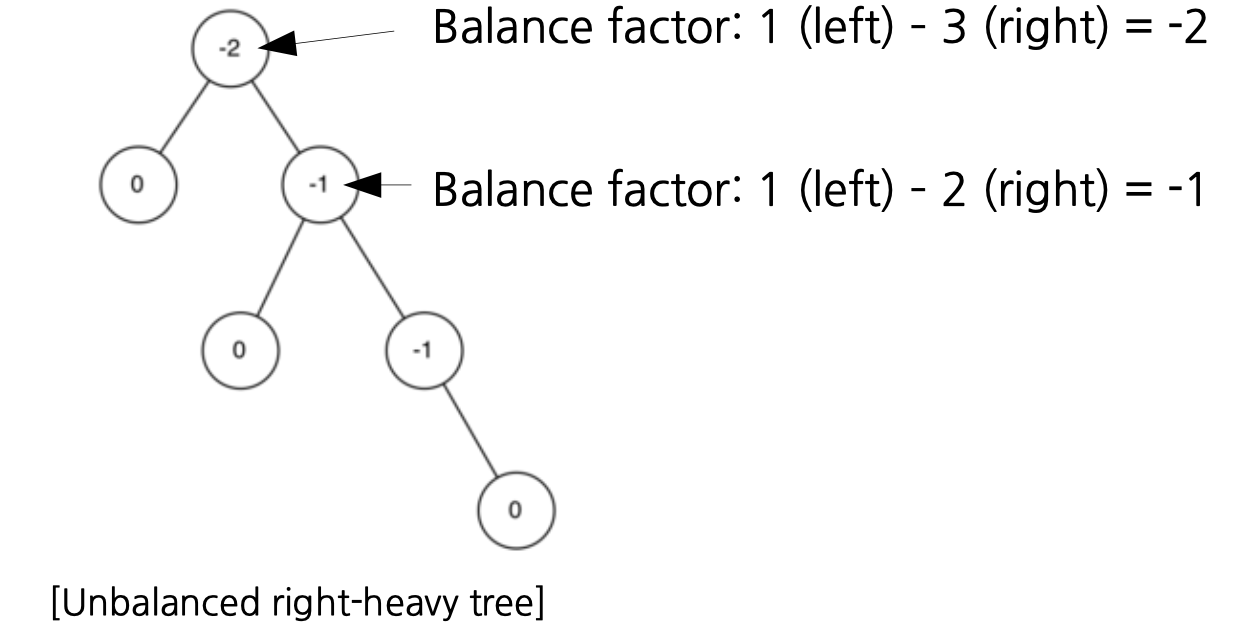
정리

Balance factor should be -1 or 0 or 1

Balance factor = height of left subtree - height of right subtree

🔄 Balancing by Rotation

◀️ Left rotation

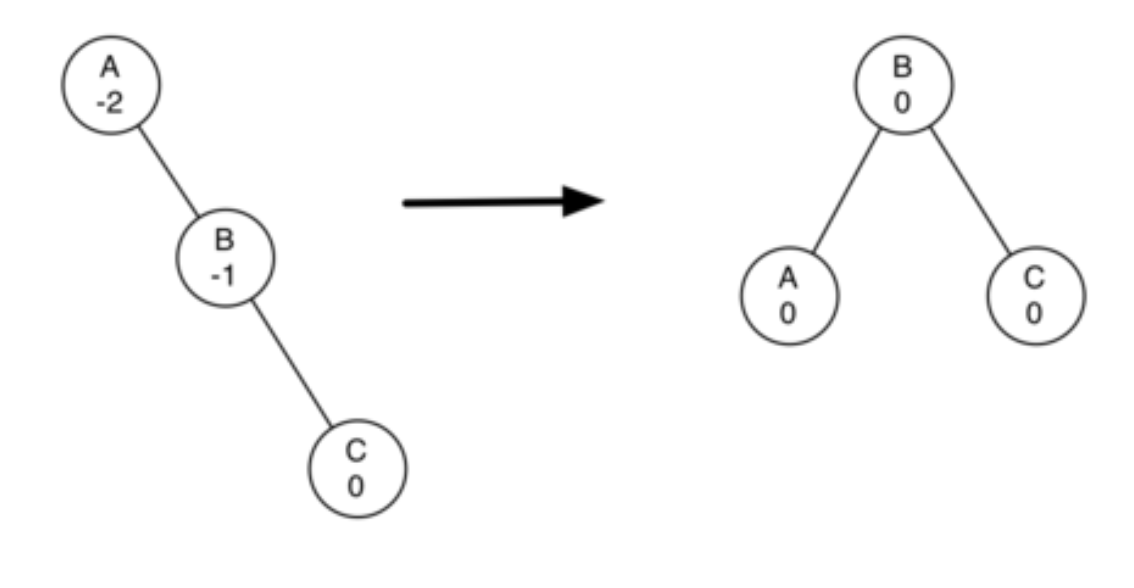
위 그림을 C가 삽입된 직후라고 가정해 봅시다. C는 자식이 없으므로, balance factor는 0입니다. 따라서 정상적으로 리턴하고 B로 올라갑니다. B의 balance factor는 -1이며, 정상적으로 리턴하고 A로 올라갑니다. A의 balance factor는 -2이므로, 불균형이 탐지되었습니다. 오른쪽 subtree가 더 무겁기 때문에, 균형을 맞춰줘야 합니다.

B를 새로운 루트로 하고, A를 B의 왼쪽 자식으로 보내면, BST property를 유지하면서 balance를 맞출 수 있습니다. B가 이미 왼쪽 자식을 갖고 있었다면 어떻게 할까요? B의 왼쪽 자식의 key값은 A의 key값보다 크기 때문에, A의 오른쪽 자식으로 보내면 됩니다. 이러한 과정을 left rotation이라 하고, 다음과 같이 정리할 수 있습니다.

Step1 : B를 새로운 루트로 선택
Step2 : A를 B의 왼쪽 자식으로 바꾸기
Step3 : B가 이미 왼쪽 자식이 있다면, 그 자식을 A의 오른쪽 자식으로 지정
Step4 : balance factor 업데이트

▶️ Right rotation

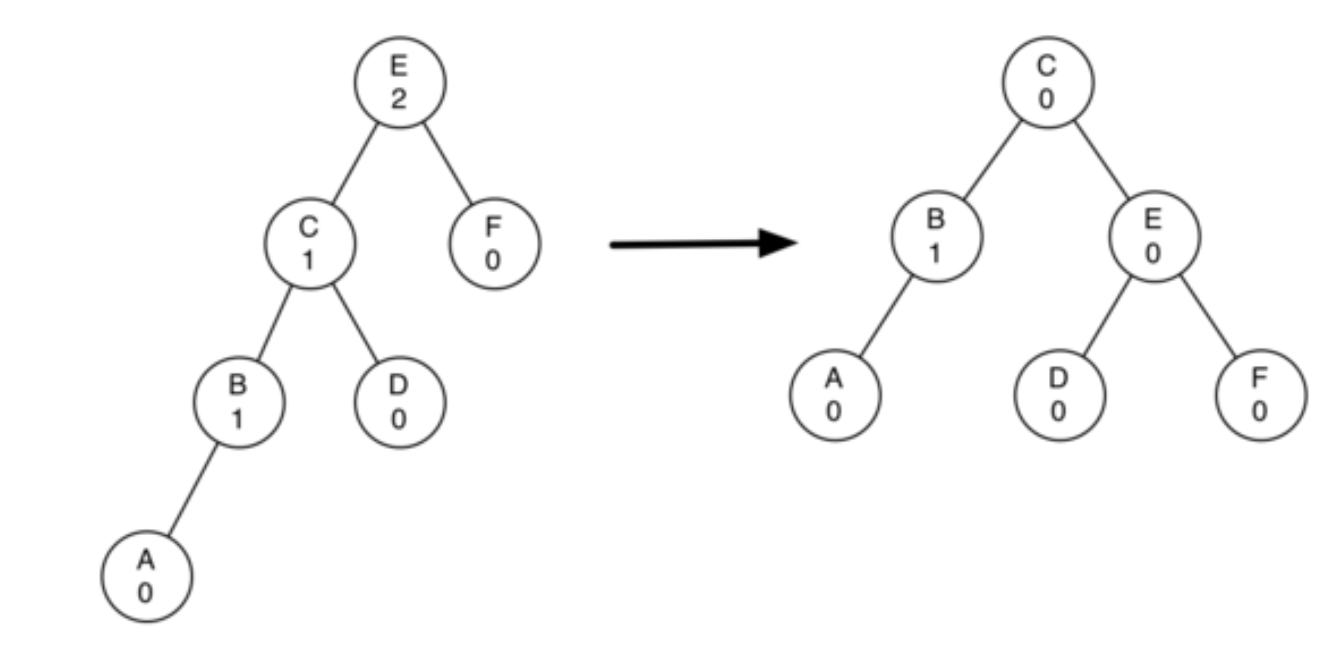
위 그림에서는 A가 삽입된 직후라고 가정해 봅시다. A가 없을 때에는, 모든 노드가 balance를 이루고 있습니다. A가 삽입된 이후, A는 자식이 없으므로 balance factor는 0이며 정상적으로 리턴하고 B로 올라갑니다. B의 balance factor는 1이며 리턴하고 C로 갑니다. C의 balance factor도 1이며 리턴하고 E로 갑니다. E의 balance factor는 2이므로, 불균형이 탐지되었습니다.

C를 새로운 루트로 하고 E를 C의 오른쪽 자식으로 보내면, BST property를 유지하면서 balance를 맞출 수 있습니다. D의 키값은 어차피 E의 키값보다 작으므로, E의 왼쪽 자식으로 보내면 됩니다. 이 과정을 right rotation이라고 하며, 다음과 같이 정리할 수 있습니다.

Step1 : C를 새로운 루트로 선택
Step2 : E를 C의 오른쪽 자식으로 바꾸기
Step3 : C가 이미 오른쪽 자식이 있으면, 그 자식을 E의 왼쪽 자식으로 지정
Step4 : balance factor 업데이트

🧮 Balance factor update

left rotation 혹은 right rotation은 매번 balance factor를 업데이트합니다. balance factor는 어떻게 업데이트 할까요?

left rotation을 수행하고 마지막에 balance factor를 업데이트하는 상황을 가정해봅시다.

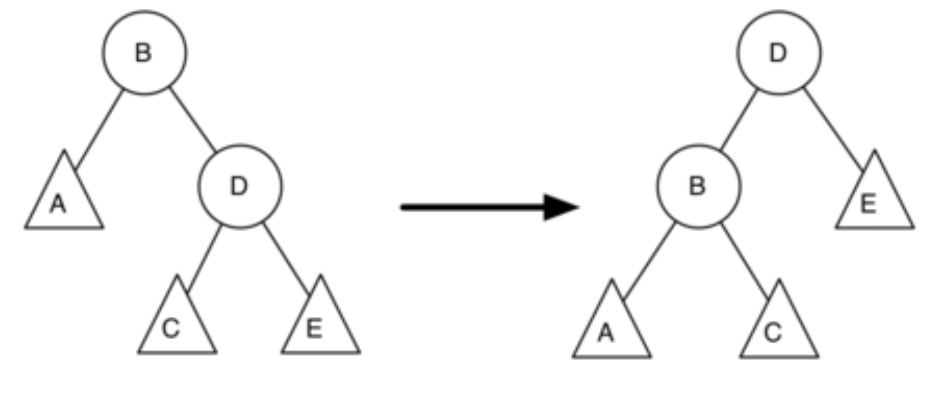
위 그림에서, A, C, E는 balance factor가 바뀌지 않습니다. B와 D만 바뀌며, 이 둘을 업데이트해야 합니다.

$h_x$ 를 노드 $x$ 의 높이라고 하겠습니다. 그럼 다음과 같이 표현할 수 있습니다.

$newBal(B) = h_A - h_C$
$oldBal(B) = h_A - h_D$

그런데 $h_D$ 는 서브 트리의 높이 중 큰 값보다 1큽니다. 즉, $1+max(h_C, h_E)$ 입니다.

$oldBal(B) = h_A - (1 + max(h_C, h_E))$

이렇게 하면 B의 새로운 balance factor는 다음과 같이 balance factor만으로 표현할 수 있습니다.

$newBal(B) - oldBal(B) = 1 + max(h_C, h_E) - h_C$
-> $newBal(B) - oldBal(B) = 1 + max(h_C - h_C, h_E - h_C)$
-> $newBal(B) - oldBal(B) = 1 + max(0, -oldBal(D))$
-> $newBal(B) - oldBal(B) = 1 - min(0, oldBal(D))$

따라서, $newBal(B) = oldBal(B) + 1 - min(0, oldBal(D))$

마찬가지로 D에 대해서도 위와 비슷한 과정을 수행하면 다음과 같습니다.

$newBal(D) = oldBal(D) + 1 + max(0, newBal(B))$

balance factor를 업데이트하는 과정은 다음의 코드로 표현할 수 있습니다.

rotRoot.balanceFactor = rotRoot.balanceFactor + 1 - min(0, newRoot.balanceFactor);
newRoot.balanceFactor = newRoot.balanceFactor + 1 + max(0, rotRoot.balanceFactor);

🛡️ Pre-Balancing

그런데, 이렇게만 하면 충분할까요? 다음 그림을 보시죠.

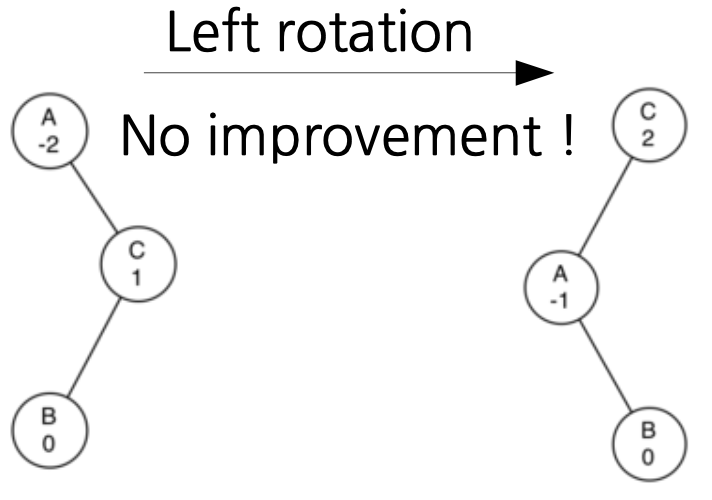
A의 balance factor가 -2이므로 left rotation을 수행합니다. C를 새로운 루트로 하고, C의 왼쪽 자식으로 A를 보냅니다. C에 이미 왼쪽 자식이 있으므로, 이 왼쪽 자식은 A의 오른쪽 자식이 됩니다. 그럼 위 그림처럼, balancing이 이루어지지 않게 됩니다.

C의 balance factor가 2이므로, 다시 right rotation을 수행하면 어떨까요? 결과는 원래대로 돌아와서 결국 balancing이 이루어지지 않게 됩니다.

이 문제를 해결하기 위해, 다음의 규칙을 따라야 합니다.

left rotation을 할 경우
만약 오른쪽 자식의 balance factor가 0보다 크다면, 오른쪽 자식에 대해 right rotation을 수행하고, 루트에 대해 left rotation한다
right rotation을 할 경우
만약 왼쪽 자식의 balance factor가 0보다 작다면, 왼쪽 자식에 대해 left rotaion하고, 루트에 대해 right rotation한다

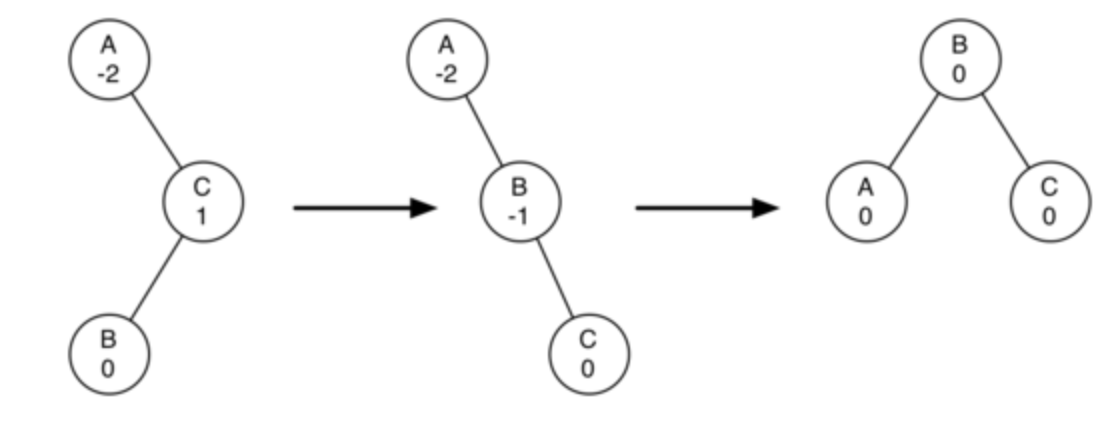
위 그림은 A를 left rotation하기 전에, C에 대해 right rotation하는 결과를 보여줍니다.

마무리 🚀

Balanced Binary Search Tree는 삽입 혹은 삭제가 이루어질 때, Balancing 작업을 통해 항상 왼쪽 서브트리와 오른쪽 서브트리의 높이 차이를 일정하게 유지하여 트리의 시간복잡도를 $O(log N)$ 으로 보장합니다.
이때, Balancing 작업(회전 연산)의 시간복잡도는 $O(1)$ 입니다.
- Balancing은 불균형이 발생한 노드에서만 수행되며, 한 번의 회전은 상수 시간에 완료됩니다.
Balanced BST는 C++의 std::map(TreeMap)과 같은 Ordered Map 자료구조의 구현에 사용됩니다.
- 이를 통해 key-value pair를 정렬된 상태로 관리하며, 삽입/삭제/검색 모두 $O(log N)$ 의 시간복잡도로 동작합니다.